Svelare i Segreti del Metallo: Perché il 3D Batte il 2D nell’Analisi Post-Strizione con il VFM

Ciao a tutti! Oggi voglio parlarvi di qualcosa che mi appassiona molto nel campo dell’ingegneria dei materiali: capire come si comportano i metalli quando li mettiamo sotto sforzo, specialmente le lamiere sottili che troviamo ovunque, dalle auto agli elettrodomestici. In particolare, c’è un fenomeno affascinante (e un po’ problematico per noi ingegneri) chiamato incrudimento (hardening), che descrive come un metallo diventa più resistente man mano che lo deformiamo plasticamente.

Capire bene l’incrudimento è fondamentale, soprattutto perché molti processi di formatura dei metalli spingono il materiale ben oltre il punto in cui inizia a deformarsi in modo non uniforme. Se vogliamo simulare questi processi al computer (usando software di analisi agli elementi finiti, o FEA), dobbiamo fornire al software una curva sforzo-deformazione reale il più accurata possibile. Altrimenti, le nostre simulazioni saranno… beh, poco utili!

Il Problema della Strizione (Necking)

Il guaio inizia dopo che il materiale raggiunge il suo allungamento uniforme massimo. Nelle classiche prove di trazione uniassiale, osserviamo un fenomeno chiamato strizione diffusa (diffuse necking): la deformazione smette di essere uniforme e si concentra in una zona specifica del provino, che inizia ad assottigliarsi. Spesso, a questa segue una strizione localizzata (localized necking), dove lo spessore diminuisce ancora più rapidamente.

In questa zona di “collo” (neck), non solo la deformazione è concentrata, ma si sviluppa anche uno stato di sforzo triassiale. Non c’è più solo lo sforzo nella direzione in cui tiriamo, ma anche sforzi nelle altre direzioni. Questo complica enormemente le cose! I metodi tradizionali, come l’uso di estensimetri, non riescono più a misurare correttamente la deformazione reale in questa zona, sottostimandola.

Certo, ci sono stati tentativi per superare questo ostacolo. Già Bridgman negli anni ’40 propose metodi analitici per correggere le misure post-strizione, ma erano complessi e spesso limitati a provini cilindrici (poco pratici per le lamiere). Altri metodi sono stati sviluppati, ma spesso richiedono provini specifici o molto lavoro sperimentale.

Entra in Scena il Metodo dei Campi Virtuali (VFM)

Negli ultimi anni, grazie all’avanzamento delle tecniche di misurazione a campo intero (come la Digital Image Correlation – DIC, che ci permette di mappare le deformazioni su tutta la superficie del campione) e ai metodi inversi, abbiamo nuovi strumenti potentissimi. Uno dei più promettenti è il Metodo dei Campi Virtuali (VFM).

Il VFM si basa sul principio dei lavori virtuali, una forma integrale dell’equilibrio meccanico. In parole povere, invece di usare gli spostamenti reali, usiamo degli “spostamenti virtuali” (campi virtuali, appunto) scelti ad arte. Il principio afferma che, in condizioni quasi-statiche e trascurando le forze di volume, il lavoro virtuale interno (dovuto agli sforzi interni e alle deformazioni virtuali) deve essere uguale al lavoro virtuale esterno (dovuto alle forze esterne applicate e agli spostamenti virtuali).

Il bello del VFM è che, usando campi virtuali opportuni, possiamo mettere in relazione diretta le misure di deformazione a campo intero con i parametri del materiale che vogliamo identificare (come quelli della legge di incrudimento), spesso senza bisogno di complesse simulazioni FEA iterative, riducendo drasticamente i costi computazionali.

2D vs 3D: La Sfida della Terza Dimensione

Fin qui tutto bene. Il VFM è stato applicato con successo per caratterizzare l’incrudimento delle lamiere sottili fino a grandi deformazioni. Ma c’è un “ma”. La maggior parte delle applicazioni del VFM su lamiere si basa su un’ipotesi bidimensionale (2D). Si usano le misure di deformazione sulla superficie del campione (ottenute ad esempio con la DIC) e si assume uno stato di sforzo piano (plane stress), ovvero si trascurano gli sforzi lungo lo spessore ((sigma_{zz}), (sigma_{xz}), (sigma_{yz}) sono considerati nulli).

Questa ipotesi funziona abbastanza bene prima della strizione, quando la lamiera è sottile rispetto alle altre dimensioni. Ma cosa succede dopo la strizione? Come abbiamo detto, nella zona del collo si sviluppa uno stato di sforzo triassiale. L’ipotesi 2D inizia a scricchiolare! Alcuni studi hanno infatti evidenziato che, dopo la strizione, il lavoro virtuale interno calcolato con l’approccio 2D non bilancia più perfettamente quello esterno, portando a una descrizione inaccurata dell’incrudimento. La ricca informazione contenuta nello stato triassiale viene persa.

E se provassimo ad usare un approccio tridimensionale (3D)? Un VFM formulato in 3D non farebbe più l’ipotesi di sforzo piano e potrebbe, in teoria, sfruttare appieno l’informazione contenuta nello stato di sforzo complesso che si sviluppa durante la strizione. Il problema è che, ad oggi, non abbiamo tecniche sperimentali mature per misurare i campi di deformazione all’interno del volume del materiale in modo semplice.

Tuttavia, con le simulazioni numeriche possiamo generare dati 3D completi. Questo ci permette di esplorare il potenziale del 3D-VFM e, soprattutto, di quantificare i limiti del 2D-VFM. Ed è proprio quello che abbiamo fatto in questo studio!

Simulazioni al Computer: Mettiamo alla Prova il VFM

Per capirci meglio, abbiamo creato un laboratorio virtuale. Abbiamo simulato al computer (usando Abaqus/Standard) una prova di trazione uniassiale su un provino con una geometria particolare, a sezione variabile. Questa forma è utile perché genera un campo di deformazione non uniforme su un’area ampia fin dall’inizio e localizza la strizione in una zona prevedibile (il centro).

Abbiamo modellato il provino in 3D, usando elementi solidi (brick a 8 nodi) e considerando tre strati di elementi lungo lo spessore. Il materiale virtuale che abbiamo usato si basa sulle caratteristiche reali di un acciaio bifasico DP780, molto comune nell’automotive, descrivendo il suo comportamento elasto-plastico con un criterio di snervamento di von Mises e una legge di incrudimento isotropa di Swift ((sigma = K(varepsilon_0 + bar{varepsilon}^p)^n)).

La cosa interessante è che abbiamo simulato la prova per diversi spessori del provino: 1.5 mm (il valore nominale per il DP780 reale), 2 mm, 2.5 mm, 3 mm, 4 mm, 6 mm, 8 mm e fino a 10 mm, mantenendo le stesse proprietà del materiale. Questo ci ha permesso di studiare l’influenza dello spessore sull’accuratezza del 2D-VFM rispetto al 3D-VFM.

Per il 3D-VFM, abbiamo usato i dati di spostamento da tutti i nodi della mesh 3D nella zona di interesse. Per il 2D-VFM, abbiamo usato solo i dati dai nodi sulla superficie ((z=0)) e abbiamo applicato le ipotesi classiche dello sforzo piano.

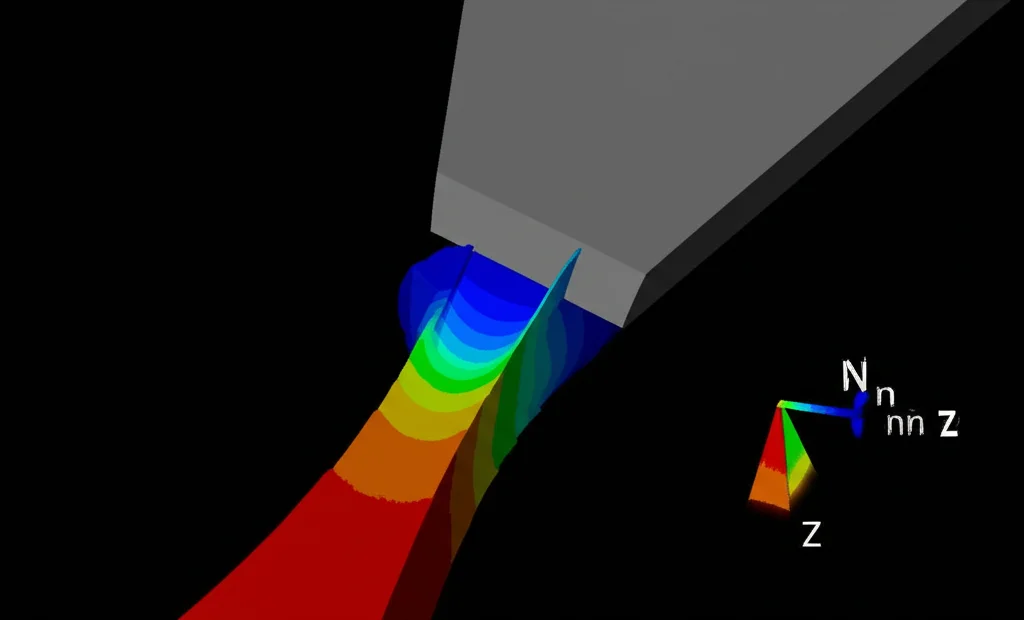
I Risultati Parlano Chiaro: Il 3D Vince (quasi) Sempre

La prima cosa che abbiamo fatto è stata confrontare il carico previsto dal VFM (calcolato a partire dal lavoro virtuale interno usando i parametri reali del materiale) con il carico di riferimento ottenuto dalla simulazione FEA. Abbiamo usato un campo virtuale specifico ((textbf{U}^{*}_1)) che permette questo calcolo diretto.

I risultati? Sorprendenti!

• Usando il 3D-VFM, l’errore relativo tra carico previsto e carico reale è stato bassissimo (inferiore allo 0.03%) per tutti gli spessori, anche ben oltre l’inizio della strizione. Il 3D-VFM predice l’evoluzione del carico in modo impeccabile.
• Usando il 2D-VFM, invece, le cose cambiano drasticamente. Per lo spessore più piccolo (1.5 mm), l’errore rimane basso fino all’inizio della strizione severa (circa 4 mm di spostamento), per poi salire rapidamente fino all’1%. Già questo potrebbe non essere accettabile per applicazioni di alta precisione. Ma il vero problema emerge con spessori maggiori: l’errore relativo cresce significativamente e molto prima nel corso della prova. Per il provino da 10 mm, l’errore raggiunge il 6% alla fine della simulazione!

L’analisi degli sforzi interni ha confermato il perché: dopo la strizione, lo sforzo normale lungo lo spessore ((sigma_{zz})) diventa non trascurabile, specialmente al centro del provino (piano mediano), e ci sono differenze significative tra gli sforzi sulla superficie e quelli al centro. Il 2D-VFM, ignorando (sigma_{zz}) e usando solo i dati superficiali, perde completamente queste informazioni cruciali, portando a errori nel calcolo del lavoro interno e, di conseguenza, nella previsione del carico. L’errore è chiaramente correlato allo spessore: più il campione è spesso, prima e più gravemente l’ipotesi 2D fallisce.

Identificazione dei Parametri: La Prova del Nove

Ma la vera prova del nove è stata usare il VFM per identificare i parametri della legge di incrudimento di Swift ((K), (sigma_0), (n)). Abbiamo usato un algoritmo di ottimizzazione (Nelder-Mead) per trovare i parametri che minimizzano la differenza tra lavoro interno ed esterno.

Abbiamo provato sia con il 2D-VFM che con il 3D-VFM, partendo dai parametri di riferimento (quelli usati nella simulazione).

• Con il 3D-VFM: In tutti i casi (1.5 mm, 3 mm, 10 mm di spessore), l’algoritmo ha ritrovato esattamente i parametri di riferimento. Bingo!
• Con il 2D-VFM: Un disastro. Per lo spessore di 1.5 mm, i parametri identificati erano leggermente diversi da quelli reali. Ma per 3 mm e 10 mm, i parametri trovati erano completamente sballati, a volte anche fisicamente irrealistici! Cercare di “correggere” l’errore del 2D-VFM modificando i parametri porta solo a un compromesso che magari migliora la previsione in una fase a scapito di un’altra, ma non rappresenta il comportamento reale del materiale.

Questo conferma che l’errore introdotto dall’ipotesi 2D dopo la strizione è tale da compromettere seriamente l’identificazione dei parametri del materiale, soprattutto per campioni non estremamente sottili.

Campi Virtuali: Manuali ma Efficaci (per Ora)

In questo studio abbiamo usato tre diversi campi virtuali definiti manualmente. Il primo ((textbf{U}^{*}_1)) è classico e lega direttamente il lavoro interno al carico esterno. Il secondo ((textbf{U}^{*}_2)) è spesso usato nel 2D-VFM e considera solo le componenti piane. Il terzo ((textbf{U}^{*}_3)), una nostra proposta per estendere il secondo al 3D, assegna pesi anche alle componenti fuori piano e varia lungo lo spessore.

Abbiamo provato diverse combinazioni di questi campi nell’identificazione 3D-VFM. I risultati sono stati consistentemente buoni: tutti hanno identificato i parametri con un errore inferiore all’1% rispetto a quelli reali, spesso ritrovando i valori esatti. L’uso del primo campo virtuale, da solo o in combinazione, sembra dare i risultati migliori, confermando l’importanza di includere l’informazione sul carico esterno. È interessante notare che per lo spessore maggiore (10 mm), il secondo campo virtuale (quello “2D esteso”) ha dato risultati leggermente peggiori, suggerendo che ignorare esplicitamente le componenti fuori piano anche nella definizione del campo virtuale può essere limitante quando queste diventano importanti.

Anche se i campi manuali hanno funzionato bene qui (con dati simulati e puliti), la ricerca futura si sta orientando verso campi virtuali generati automaticamente (es. basati sulla sensibilità) per ridurre la dipendenza dall’utente e migliorare la robustezza con dati sperimentali rumorosi.

Conclusioni e Prospettive Future

Cosa ci portiamo a casa da tutto questo? Beh, principalmente che l’ipotesi 2D, comunemente usata nel VFM per caratterizzare l’incrudimento delle lamiere, ha dei limiti ben precisi, specialmente dopo l’insorgere della strizione e per spessori non trascurabili. L’errore diventa significativo e compromette sia la previsione del comportamento meccanico sia l’identificazione accurata dei parametri del materiale.

Il 3D-VFM, invece, si è dimostrato capace di superare queste limitazioni, fornendo risultati accurati anche in condizioni di strizione severa e per diversi spessori, almeno in questo studio basato su simulazioni.

Questo lavoro è un primo passo, uno studio numerico pionieristico che quantifica i limiti del 2D-VFM e mostra il potenziale del 3D. Certo, la sfida ora è portare il 3D-VFM nel mondo reale. Servono tecniche sperimentali per ottenere misure di deformazione 3D volumetriche, oppure metodi intelligenti per ricostruire i campi 3D a partire da misure superficiali (come il metodo “internal mesh generation” citato nello studio originale).

È un campo di ricerca attivo e stimolante! Capire a fondo il comportamento dei materiali fino a rottura è cruciale per progettare componenti più leggeri, sicuri ed efficienti. E il VFM, specialmente nella sua veste 3D, sembra essere uno strumento chiave per raggiungere questo obiettivo. Spero di avervi incuriosito!

Fonte: Springer