Assi Ferroviari Merci: Quando un Graffio Minaccia la Sicurezza

Ciao a tutti! Oggi voglio parlarvi di qualcosa che forse diamo per scontato, ma che è assolutamente cruciale per la nostra economia e, soprattutto, per la nostra sicurezza: gli assi ferroviari dei treni merci pesanti. Sì, proprio quei componenti robusti che permettono a tonnellate di materie prime come carbone e minerali di ferro di viaggiare su rotaia. Pensateci, questi treni sono fondamentali, specialmente in paesi grandi, e aiutano anche a ridurre le emissioni di carbonio rispetto ad altri trasporti. Ma cosa succede se qualcosa va storto?

L’Importanza Nascosta degli Assi Merci

Spesso pensiamo che gli assi dei treni passeggeri siano i più critici, ma quelli dei treni merci non sono da meno. Immaginate un deragliamento causato dalla rottura di un asse mentre il treno trasporta sostanze pericolose, petrolio greggio o liquidi tossici. Le conseguenze potrebbero essere catastrofiche, non solo interrompendo il trasporto ma causando disastri ambientali e mettendo a rischio vite umane. Tra il 1998 e il 2002, solo in Nord America, ci sono stati ben 52 incidenti dovuti a rotture di assi merci. Questo ci fa capire quanto sia vitale garantire l’integrità strutturale e l’affidabilità di questi componenti.

Il Limite della Progettazione Tradizionale

Tradizionalmente, gli assi ferroviari venivano progettati basandosi sul concetto di “vita sicura”, utilizzando le curve di Wöhler (le famose curve S-N) per garantire una vita infinita, o almeno fino a 10 milioni di cicli. Questo approccio è ancora un riferimento fondamentale, ma la realtà è più complessa. Durante il lungo servizio, gli assi sono soggetti a condizioni ambientali difficili e possono sviluppare imperfezioni, sia intrinseche (legate al materiale) che estrinseche (causate dall’uso). Parliamo di ammaccature, graffi, vaiolature da corrosione e persino usura da contatto (fretting) nelle sedi delle ruote. Questi difetti, anche se piccoli, agiscono come punti deboli, concentrando gli sforzi e diventando potenziali inneschi per le cricche di fatica.

Entra in Gioco la Tolleranza al Danno

Ecco perché negli ultimi vent’anni si è iniziato a parlare sempre più di tolleranza al danno. Questo approccio non assume che il componente sia perfetto per tutta la sua vita, ma piuttosto valuta come si comporta *in presenza* di difetti. L’obiettivo è garantire che, anche se un difetto si forma o cresce, non porti a una rottura catastrofica prima che possa essere rilevato durante la manutenzione. Sebbene questo concetto sia stato studiato abbastanza per i treni ad alta velocità, la letteratura specifica sugli assi merci pesanti è ancora limitata. Ed è qui che entra in gioco il nostro lavoro.

Il Nostro Studio: Mettere alla Prova l’Acciaio AAR-CM

Nel nostro studio, ci siamo concentrati sull’acciaio AAR-CM, un tipo di acciaio al carbonio medio comunemente usato per questi assi pesanti, rinforzato con vanadio per migliorarne la resistenza. Abbiamo preso dei campioni da un asse reale e li abbiamo sottoposti a test di fatica per capire come reagiscono in presenza di difetti specifici.

Creare Difetti Artificiali per Capire Quelli Reali

Poiché i difetti reali sono irregolari e difficili da replicare esattamente, abbiamo creato dei difetti artificiali controllati sui nostri provini. Abbiamo usato due tipi principali:

• Intagli semicircolari: Realizzati con elettroerosione (EDM) con raggi variabili (da 0.1 mm a 1.0 mm). Questi simulano difetti come le vaiolature.
• Intagli a gola circonferenziale: Realizzati per rettifica con raggi di fondo diversi (0.04 mm, 0.1 mm, 0.5 mm). Questi rappresentano graffi o solchi.

Abbiamo poi sottoposto questi provini a test di fatica a flessione rotante a quattro punti, un metodo standard per simulare le sollecitazioni subite da un asse in servizio.

Valutare gli Intagli Semicircolari: Il Modello di El Haddad e la Sorpresa

Per gli intagli semicircolari, abbiamo cercato di prevedere il limite di fatica (cioè la massima sollecitazione che il materiale può sopportare per un numero elevato di cicli senza rompersi) usando la teoria della meccanica della frattura, in particolare il diagramma di Kitagawa–Takahashi (K-T) e il modello di El Haddad. Questo modello cerca di collegare la resistenza del materiale liscio con quella di un materiale criccato, introducendo una “lunghezza di cricca fittizia” (a₀).

Qui abbiamo avuto una sorpresa interessante. Il modello di El Haddad, spesso usato per valutare l’effetto dei piccoli difetti, si è rivelato non conservativo per i nostri intagli più piccoli. In pratica, prevedeva un limite di fatica *più alto* di quello che abbiamo misurato sperimentalmente. Perché? La risposta sembra risiedere nell’effetto di chiusura della cricca.

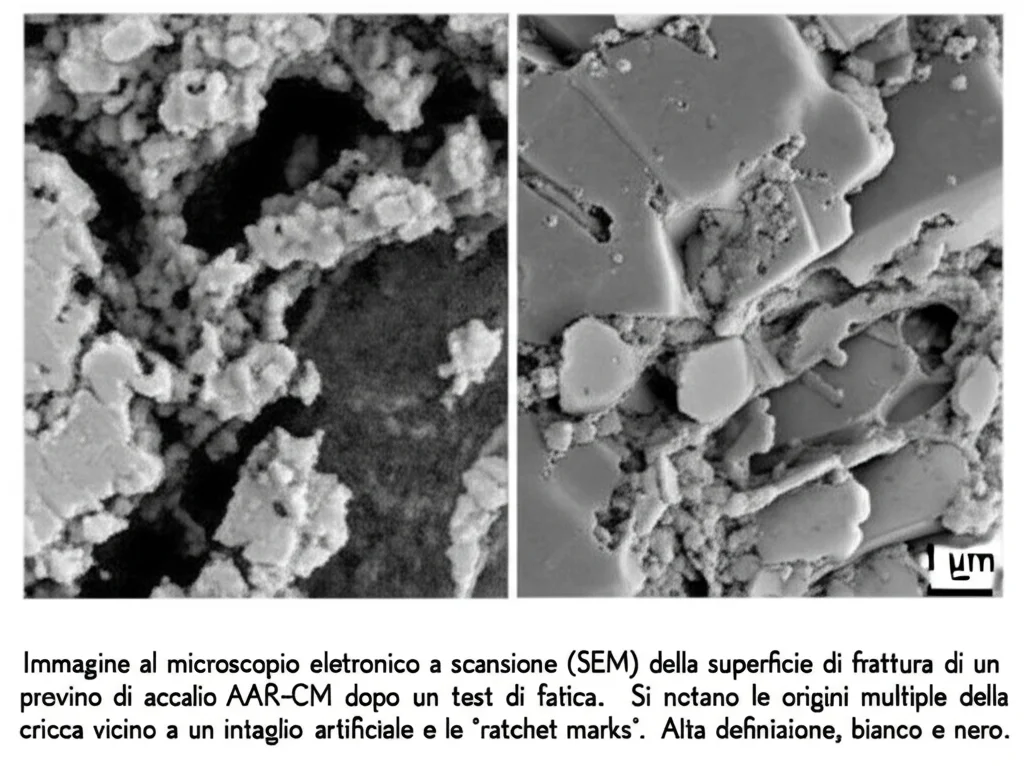
Quando una cricca si propaga, specialmente sotto carichi ciclici, le superfici della cricca stessa possono entrare in contatto durante la fase di scarico del ciclo. Questo contatto “chiude” parzialmente la cricca, riducendo l’effettiva sollecitazione alla sua punta e rallentandone la propagazione. Questo effetto non è istantaneo, ma si sviluppa man mano che la cricca cresce. Se la cricca parte da un difetto preesistente (come i nostri intagli), l’effetto di chiusura si sviluppa in modo diverso rispetto a una cricca che parte da una superficie liscia. Il modello di El Haddad non cattura appieno questa dinamica complessa, portando a previsioni ottimistiche per difetti piccoli. Questo ci dice che dobbiamo essere cauti e considerare attentamente l’effetto di chiusura per valutazioni affidabili.

Analizzare gli Intagli a Gola: La Teoria della Distanza Critica (TCD)

Per gli intagli a gola circonferenziale, abbiamo tracciato le curve S-N (sollecitazione vs numero di cicli a rottura) e abbiamo cercato di correlarle usando la Teoria della Distanza Critica (TCD). La TCD è un approccio interessante perché, invece di guardare solo lo stress nel punto più critico (la punta dell’intaglio), considera lo stress medio su una piccola distanza (la “distanza critica”, L) o in un punto a quella distanza. Questo spesso fornisce previsioni più accurate per i componenti intagliati.

Abbiamo calcolato la distanza critica L per il nostro acciaio AAR-CM (circa 0.11 mm) e abbiamo provato a usarla come costante. I risultati non erano perfetti: le curve S-N dei provini intagliati non si sovrapponevano bene a quella del provino liscio.

Allora abbiamo provato un approccio più avanzato: considerare la distanza critica L non come una costante, ma come una variabile dipendente dalla vita a fatica. Questo ha funzionato meglio! Abbiamo ottenuto curve S-N “efficaci” quasi parallele tra loro per i diversi tipi di provini. Tuttavia, non siamo riusciti a farle collassare tutte in un’unica curva maestra. Probabilmente, la complessa distribuzione degli sforzi dovuta alla combinazione della flessione generale e della concentrazione locale dell’intaglio gioca un ruolo che la TCD, nella sua forma attuale, fatica a catturare completamente in questi casi di flessione rotante. È sicuramente un’area promettente per ricerche future!

L’Effetto Scala: Perché un Provino non è un Asse Intero

Un altro punto fondamentale emerso è l’effetto scala. I nostri provini sono molto più piccoli di un asse ferroviario reale. Sotto flessione, il gradiente di stress (cioè come lo stress cambia dalla superficie verso il centro) è molto più pronunciato in un piccolo provino che in un grande asse. Questo significa che, a parità di intaglio superficiale e di stress nominale applicato, lo stress locale alla punta dell’intaglio sul provino potrebbe essere inferiore a quello sull’asse reale. Di conseguenza, il limite di fatica misurato sui provini potrebbe essere *superiore* a quello di un asse reale con lo stesso difetto. Bisogna quindi fare molta attenzione quando si trasferiscono i risultati dai test su piccola scala ai componenti reali.

Cosa Abbiamo Imparato (Conclusioni Provvisorie)

Insomma, questo viaggio nel mondo della fatica degli assi ferroviari ci ha insegnato alcune cose importanti:

• L’acciaio AAR-CM ha una buona resistenza alla propagazione delle cricche lunghe (soglia di 15.45 MPa·√m), superiore a quella di alcuni acciai usati per l’alta velocità, ma l’approccio basato solo sulla soglia delle cricche lunghe non basta per i piccoli difetti.
• Il modello di El Haddad può essere ottimista (non conservativo) per piccoli difetti (< 1 mm nel nostro caso), perché non tiene conto adeguatamente dello sviluppo dell'effetto di chiusura della cricca.
• La Teoria della Distanza Critica (TCD), specialmente se si considera la distanza critica come variabile, è promettente per correlare i dati di fatica di provini con intagli diversi, ma necessita di ulteriori affinamenti per i casi complessi come la flessione rotante.
• L’effetto scala è cruciale: i risultati sui provini devono essere interpretati con cautela quando applicati ad assi reali.

Il nostro lavoro fornisce indicazioni utili per la valutazione della tolleranza al danno, ma la strada è ancora lunga. Servono ulteriori studi, magari su assi in scala reale e con difetti più simili a quelli che si trovano in servizio (corrosione, graffi irregolari), per rendere le nostre ferrovie merci ancora più sicure. La prossima volta che vedrete passare un lungo treno merci, pensate a quanta ingegneria e scienza ci sono dietro per far sì che tutto fili liscio, rotaia dopo rotaia!

Fonte: Springer