Monotonia a Pezzi: Decifrare le Tendenze Nascoste nei Dati con le Famiglie Esponenziali

Ciao a tutti, appassionati di dati e di come estrarre significato dal caos apparente! Oggi voglio parlarvi di un’avventura statistica affascinante in cui mi sono imbattuto (metaforicamente parlando, ovviamente!). Riguarda qualcosa che, a prima vista, potrebbe sembrare un po’ tecnico – la stima monotona a tratti in famiglie esponenziali a un parametro – ma fidatevi, ha implicazioni pratiche davvero interessanti.

Avete mai notato come certi fenomeni sembrano seguire una tendenza, magari crescente o decrescente, ma non in modo perfettamente lineare o costante? Pensate alla curva dose-risposta di un farmaco, o alle curve di domanda/offerta in economia. Spesso, ci aspettiamo una certa monotonicità: all’aumentare della dose, l’effetto aumenta (o diminuisce); all’aumentare del prezzo, la domanda cala.

La statistica ha strumenti potenti per gestire queste situazioni, come la regressione isotonica. Immaginate di avere una serie di osservazioni (ad esempio, medie campionarie) e volete stimare i veri valori medi sottostanti, sapendo che questi dovrebbero essere in ordine crescente (o decrescente). La regressione isotonica fa proprio questo, trovando la migliore sequenza monotona che si adatta ai dati. L’algoritmo classico per farlo si chiama PAVA (Pool Adjacent Violators Algorithm), un nome un po’ aggressivo ma che descrive bene come “fonde” i valori vicini che violano la monotonia.

Il Problema: Quando la Monotonia si Spezza

Ma ecco il punto cruciale: la realtà è spesso più… “frastagliata”. A volte, una tendenza monotona potrebbe invertirsi bruscamente in alcuni punti, per poi riprendere. Pensate a uno spettro di frequenze che è generalmente decrescente ma presenta dei picchi isolati, o a un tasso di mortalità che cala con l’età ma ha un improvviso aumento a causa di un fattore specifico (come vedremo dopo!).

Qui entra in gioco la cosiddetta regressione quasi isotonica (nearly isotonic regression), un concetto introdotto da Tibshirani e colleghi nel 2011, inizialmente per dati Normali (Gaussiano). L’idea è di permettere alla sequenza stimata di violare la monotonia, ma “pagando un prezzo” per ogni violazione. Questo prezzo è controllato da un parametro di regolarizzazione, che chiameremo λ (lambda).

Se λ è zero, non c’è penalità e otteniamo semplicemente i dati originali. Se λ è molto grande, la penalità è così alta che l’algoritmo forza una monotonia perfetta, tornando alla regressione isotonica classica. Il bello sta nel trovare il giusto valore di λ che catturi le vere “rotture” nella monotonia senza essere ingannato dal rumore casuale dei dati.

La Nostra Sfida: Oltre i Dati Normali

Il lavoro di Tibshirani era fantastico, ma focalizzato su dati distribuiti normalmente. E se i nostri dati seguissero altre distribuzioni? Molti fenomeni reali non sono ben descritti da una curva a campana. Pensiamo a:

• Conteggi (es. numero di successi in N prove): distribuzione Binomiale
• Eventi rari (es. numero di incidenti in un periodo): distribuzione di Poisson
• Varianze o somme di quadrati: distribuzione Chi-quadrato (magari scalata)

Queste, insieme alla Normale e altre, appartengono a una grande e versatile “famiglia” matematica chiamata famiglie esponenziali a un parametro. La sfida che ci siamo posti è stata: possiamo estendere l’idea della regressione quasi isotonica a *tutte* queste distribuzioni?

La Soluzione: Un Algoritmo Generale e Intelligente

La risposta è sì! Abbiamo sviluppato un metodo e un algoritmo efficiente per stimare sequenze monotone a tratti per dati provenienti da queste famiglie esponenziali generali. Come abbiamo fatto?

Abbiamo preso l’algoritmo PAVA modificato di Tibshirani e lo abbiamo generalizzato. Un trucco chiave è stato sfruttare la cosiddetta dualità tra i “parametri naturali” (θ, quelli che compaiono direttamente nella formula della distribuzione esponenziale) e i “parametri di aspettazione” (η, che rappresentano il valore atteso dei dati). Questa dualità ci permette di lavorare in uno spazio dove i calcoli diventano più gestibili.

Il nostro algoritmo, che abbiamo chiamato Algorithm 1 nel paper originale, funziona in modo simile al PAVA modificato: parte dai dati grezzi, identifica i punti in cui la monotonia è violata e, progressivamente, fonde blocchi adiacenti di dati. La differenza principale è che tiene conto dei “pesi” specifici (w) associati a ciascuna osservazione, pesi che dipendono dalla particolare distribuzione nella famiglia esponenziale (ad esempio, il numero di prove N per la Binomiale).

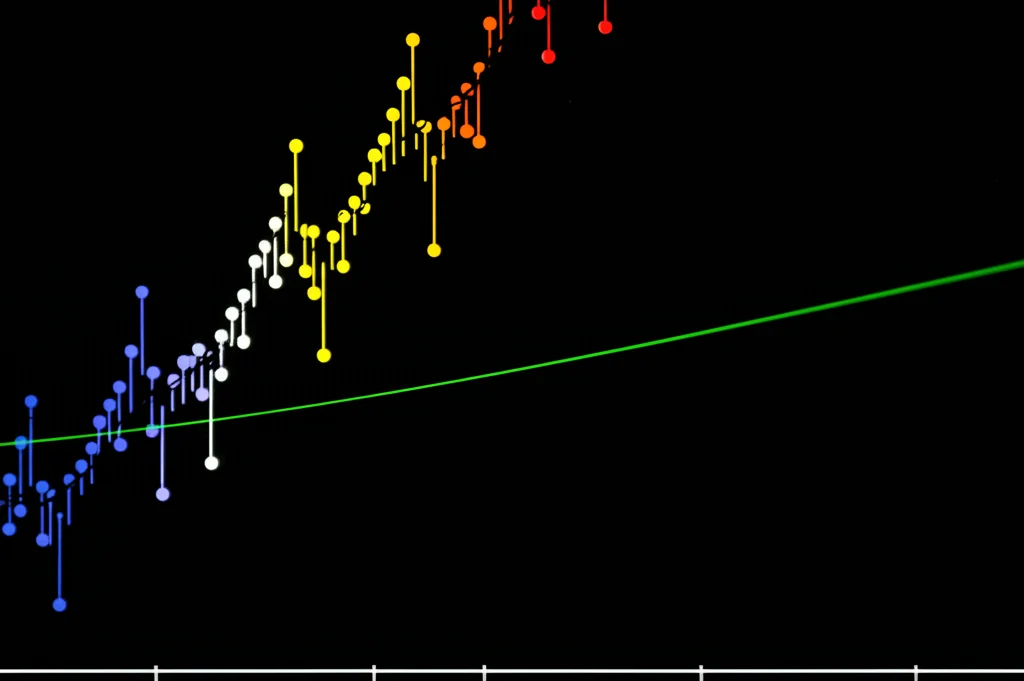
L’algoritmo non solo calcola la stima per un dato λ, ma traccia l’intero “percorso di regolarizzazione”, mostrandoci come la stima cambia al variare di λ e identificando i valori critici (knots) dove due blocchi si fondono. Questo è fondamentale, perché ci permette di scegliere il λ migliore.

Scegliere λ: Il Criterio d’Informazione

Ah, la scelta di λ! È sempre il dilemma con i metodi regolarizzati. Come trovare il bilanciamento perfetto tra adattamento ai dati e semplicità del modello (in questo caso, numero di “pezzi” monotoni)?

Abbiamo proposto di usare un criterio d’informazione, simile al famoso AIC (Akaike Information Criterion). L’idea si basa su un risultato interessante: per la regressione quasi isotonica normale, il numero di “pezzi” distinti nella stima finale (K_λ) è una stima non distorta dei gradi di libertà effettivi del modello. In parole povere, ci dice quanto è complesso il nostro modello.

Abbiamo esteso questa idea alle famiglie esponenziali generali. Il nostro AIC proposto bilancia la bontà di adattamento del modello ai dati (misurata tramite la discrepanza di Kullback-Leibler, una misura di “distanza” tra distribuzioni di probabilità) con la complessità del modello, penalizzando i modelli con troppi pezzi monotoni (cioè, K_λ).

In pratica, calcoliamo l’AIC per ogni valore critico di λ trovato dal nostro algoritmo e scegliamo il λ che minimizza l’AIC. Le simulazioni che abbiamo condotto (ad esempio, con dati Binomiali) mostrano che questo approccio funziona sorprendentemente bene nel rilevare i veri punti di cambiamento nella sequenza dei parametri, in modo guidato dai dati stessi! Sembra che, anche se la derivazione teorica rigorosa è più complessa, usare K_λ come misura di complessità sia una buona approssimazione pratica, specialmente quando le distribuzioni non sono “troppo lontane” dalla normalità.

Applicazioni nel Mondo Reale: Dove la Monotonia a Pezzi Fa la Differenza

Ok, tutto molto bello, ma a cosa serve concretamente? Vediamo tre esempi che abbiamo esplorato:

Applicazione 1: Caccia alle Frequenze Nascoste (Stima dello Spettro)

Nell’analisi delle serie temporali, lo spettro di potenza ci dice quali frequenze (periodicità) sono dominanti in un segnale. Spesso, lo spettro tende a decrescere all’aumentare della frequenza (come nel rumore “1/f”), ma può avere dei picchi netti corrispondenti a periodicità specifiche. Stimare uno spettro del genere è un problema perfetto per il nostro metodo! Abbiamo applicato la nostra tecnica (usando la distribuzione Chi-quadrato, appropriata per i periodogrammi) ai dati storici delle macchie solari (dati di Wolfer). Il metodo ha correttamente identificato la tendenza generale decrescente, evidenziando però il famoso picco corrispondente al ciclo di circa 11 anni delle macchie solari.

Applicazione 2: Capire Causa ed Effetto (Inferenza Causale con RDD)

Il Regression Discontinuity Design (RDD) è una tecnica usata in econometria e altre scienze sociali per stimare l’effetto causale di un intervento che viene assegnato in base al superamento di una soglia. Un esempio classico è l’effetto dell’età minima legale per bere alcolici sulla mortalità per incidenti stradali. Ci si aspetta una tendenza generale della mortalità con l’età, ma un “salto” improvviso proprio all’età legale. Abbiamo applicato il nostro metodo (con la distribuzione di Poisson, adatta a conteggi di eventi come gli incidenti mortali) ai dati sulla mortalità per incidenti stradali negli USA per età (in mesi). Il metodo ha stimato una tendenza generale (in questo caso, decrescente dopo una certa età), ma ha chiaramente identificato un brusco aumento proprio a 21 anni, l’età legale per bere. Questo suggerisce che il nostro approccio potrebbe essere utile in RDD, specialmente se la soglia stessa non è nota a priori.

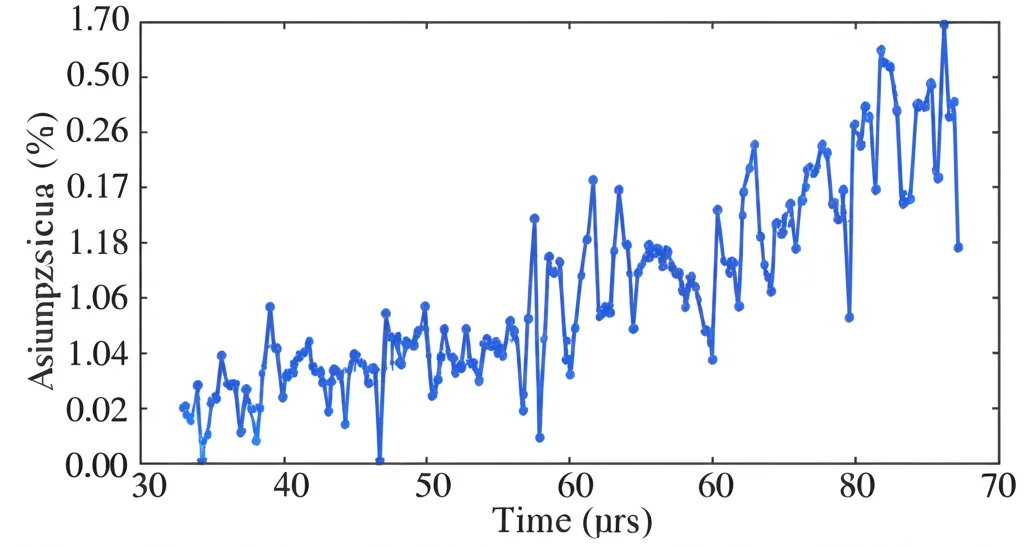
Applicazione 3: Valutare l’Errore nelle Simulazioni (Quantificazione dell’Errore ODE)

Quando risolviamo equazioni differenziali ordinarie (ODE) al computer (ad esempio, per simulare sistemi fisici o biologici), introduciamo inevitabilmente un errore di discretizzazione dovuto al fatto che avanziamo nel tempo a passi finiti. Capire come questo errore si accumula e si comporta è cruciale, specialmente in simulazioni complesse o in problemi inversi come l’assimilazione dati. Abbiamo proposto un modo per quantificare questo errore modellando le varianze dell’errore nel tempo. Ci aspettiamo che l’errore tenda ad accumularsi (quindi la varianza dovrebbe crescere), ma se il sistema simulato ha un comportamento periodico (come nel modello di FitzHugh-Nagumo, che descrive l’eccitabilità neuronale), anche l’errore potrebbe mostrare delle “ondulazioni” o cali periodici. Applicando il nostro metodo (con la distribuzione Chi-quadrato, legata ai residui quadratici) alla stima della varianza dell’errore nella simulazione del modello FN, abbiamo visto che la stima monotona a tratti cattura molto meglio l’andamento complesso dell’errore (accumulo generale con fluttuazioni periodiche) rispetto a una semplice stima isotonica crescente. Questo potrebbe aiutarci a capire meglio l’affidabilità delle nostre simulazioni.

Conclusioni e Prospettive Future

Cosa ci portiamo a casa da tutto questo? Abbiamo esteso con successo la regressione quasi isotonica alle famiglie esponenziali a un parametro, fornendo un algoritmo efficiente e un criterio basato sui dati (AIC) per scegliere il parametro di regolarizzazione. Questo ci permette di analizzare dati con tendenze monotone “interrotte” in una vasta gamma di contesti, come dimostrato dalle applicazioni.

Certo, c’è ancora strada da fare. Sarebbe interessante estendere questo approccio a situazioni più complesse dove l’ordine non è semplice (ad esempio, dati su griglie multidimensionali o grafi), il che potrebbe avere applicazioni in RDD spaziale o nell’analisi di errori in PDE. Inoltre, si potrebbe lavorare per derivare criteri d’informazione ancora più accurati, specialmente per distribuzioni lontane dalla normalità, o studiare le proprietà teoriche come i limiti di rischio. L’inferenza Bayesiana per quantificare l’incertezza è un’altra direzione promettente.

Ma per ora, spero di avervi mostrato come un’idea apparentemente semplice – permettere alla monotonia di “spezzarsi” in modo controllato – possa aprire nuove porte nell’analisi di dati complessi provenienti da diverse fonti. È il bello della statistica: trovare strutture nascoste e dare un senso più profondo ai numeri!

Fonte: Springer