Stampa 3D Metallo: Il Segreto per Simulazioni Termiche Super Accurate (Senza Mal di Testa!)

Ciao a tutti! Oggi voglio parlarvi di qualcosa che mi appassiona tantissimo: la stampa 3D di metalli, o più tecnicamente, la Fusione Laser su Letto di Polvere (PBF-LB). Immaginate di poter creare oggetti metallici complessi, strato dopo strato, usando un laser potentissimo che fonde polveri metalliche finissime. Fantascienza? No, è realtà! Ma c’è un “ma”.

La Sfida: Capire Cosa Succede Davvero Là Dentro

Il problema è che questo processo è un po’ una “scatola nera”. Avviene a temperature altissime, è incredibilmente veloce e l’area di lavoro è piccolissima e difficile da osservare direttamente. Capire esattamente come il calore si diffonde, come si forma la pozza fusa e come solidifica il metallo è fondamentale per ottenere pezzi di alta qualità, senza difetti. E qui entrano in gioco le simulazioni al computer.

Noi ricercatori usiamo modelli numerici per “virtualizzare” il processo, cioè per ricrearlo in un ambiente digitale dove possiamo analizzare ogni dettaglio, come i campi di temperatura o le caratteristiche della pozza fusa. È un po’ come avere dei superpoteri per guardare dentro la macchina PBF-LB mentre lavora!

Il Dilemma: Velocità vs. Precisione nelle Simulazioni

Ora, per simulare tutto *perfettamente*, dovremmo includere nei nostri modelli anche la fluidodinamica, cioè il modo in cui il metallo fuso si muove nella pozza. Pensate a micro-correnti causate da differenze di tensione superficiale (il famoso effetto Marangoni), che influenzano tantissimo come il calore si distribuisce. Il problema? Includere la fluidodinamica rende le simulazioni *estremamente* complesse e lente, richiedendo una potenza di calcolo enorme.

Per questo motivo, spesso si preferisce usare modelli più semplici, che si concentrano solo sul trasporto del calore (simulazioni termiche) e ignorano volutamente i movimenti del fluido. Questi modelli sono molto più veloci e richiedono meno risorse, il che è ottimo per fare tante prove e ottimizzare i parametri di processo. Ma, come potete immaginare, questa semplificazione ha un costo: la precisione. Se non consideriamo come si muove il metallo fuso, la nostra simulazione potrebbe non rappresentare fedelmente la realtà, e i risultati potrebbero essere poco affidabili. Un bel dilemma, vero?

La Nostra Idea: Rendere “Intelligente” la Sorgente Laser Virtuale

Ed è qui che entra in gioco il nostro lavoro. Ci siamo chiesti: e se potessimo rendere i nostri modelli termici semplici *più intelligenti*, in modo che tengano conto implicitamente degli effetti della fluidodinamica, senza doverla simulare esplicitamente? La risposta che abbiamo esplorato sta nell’adattare i parametri della sorgente di energia laser nel modello.

In pratica, quando simuliamo il laser, usiamo un modello matematico che descrive come l’energia viene depositata nel materiale. Di solito si usa un profilo Gaussiano (a forma di campana) che decade esponenzialmente sia sulla superficie che in profondità. I parametri chiave qui sono l’assorbività (quanta energia laser viene effettivamente assorbita dal materiale) e la profondità di penetrazione (quanto in profondità arriva l’energia).

Normalmente, questi parametri vengono considerati costanti. Ma noi sappiamo che nella realtà non è così! L’assorbività e la profondità effettiva con cui il laser interagisce dipendono moltissimo dalla potenza del laser e dalla velocità con cui si muove (la velocità di scansione). Perché? Perché a seconda di questi parametri, si possono formare delle piccole cavità (keyhole) nel metallo fuso, dove il laser viene riflesso più volte, aumentando l’assorbimento effettivo e cambiando il modo in cui il calore penetra. Questi sono proprio gli effetti legati alla dinamica del fuso che i modelli semplici ignorano!

La nostra idea, quindi, è stata quella di rendere l’assorbività (`η_Leff`) e la profondità di penetrazione (`δ_Leff`) nel nostro modello non più costanti, ma *variabili*, dipendenti proprio dalla potenza laser (P) e dalla velocità di scansione (v_foc). In questo modo, la nostra sorgente di energia “adattiva” può mimare, almeno in parte, gli effetti complessi che accadono nella realtà, migliorando l’accuratezza della simulazione termica.

Come Abbiamo Fatto: Un Mix di Simulazioni e Dati Reali

Per mettere in pratica questa idea, abbiamo usato un software di simulazione agli elementi finiti (FEA), nel nostro caso COMSOL Multiphysics. Abbiamo costruito un modello termico mesoscopico (cioè alla scala della pozza fusa) per il processo PBF-LB, includendo tutti i modelli matematici necessari per descrivere come il calore si trasporta nel materiale (sia in polvere che solido/fuso), come l’energia viene persa per evaporazione, convezione (flusso di gas inerte) e radiazione. Abbiamo usato come materiale di esempio una lega molto comune nella stampa 3D, l’AlSi10Mg (una lega di alluminio).

Il cuore del lavoro è stato confrontare i risultati delle nostre simulazioni con dati provenienti da esperimenti reali. Nello specifico, abbiamo usato dei modelli di regressione basati su dati sperimentali pubblicati in letteratura (da Hanemann [35]), che permettono di calcolare la larghezza e la profondità della traccia fusa reale in funzione dei parametri di processo (P e v_foc).

Abbiamo quindi lanciato tantissime simulazioni, variando sistematicamente:

• La potenza del laser (P)
• La velocità di scansione (v_foc)
• L’assorbività efficace nel modello (`η_Leff`)
• La profondità di penetrazione efficace nel modello (`δ_Leff`)

Per ogni combinazione, abbiamo misurato la larghezza (`β_sim`) e la profondità (`δ_sim`) della traccia fusa simulata. L’obiettivo era trovare, per ogni coppia di (P, v_foc) reali, la coppia di (`η_Leff`, `δ_Leff`) che rendesse le dimensioni della traccia simulata uguali a quelle previste dai modelli basati sugli esperimenti reali. Abbiamo cercato l’intersezione, il punto “magico” in cui simulazione e realtà combaciavano perfettamente per entrambe le dimensioni (larghezza e profondità) contemporaneamente.

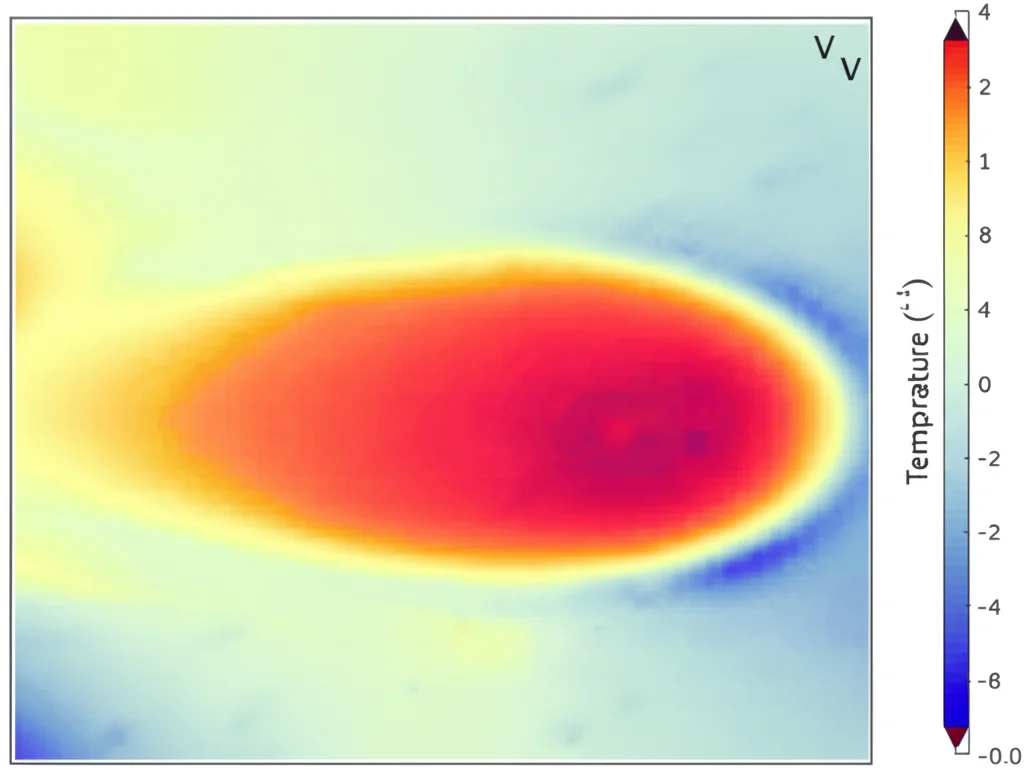
I Risultati: Simulazioni Più Accurate e Coerenti

E i risultati sono stati davvero incoraggianti! Abbiamo trovato che effettivamente esistono delle combinazioni specifiche di `η_Leff` e `δ_Leff` che permettono alle nostre simulazioni termiche semplificate di riprodurre con grande accuratezza le dimensioni reali della traccia fusa, per diverse condizioni di processo.

La cosa più interessante è che abbiamo confermato la nostra ipotesi: i valori “efficaci” di assorbività e profondità di penetrazione non sono costanti, ma cambiano con i parametri di processo. In particolare, abbiamo osservato che per densità di energia più alte (cioè alta potenza e/o bassa velocità), servono valori di `η_Leff` e `δ_Leff` più elevati per far combaciare simulazione e realtà. Questo è perfettamente coerente con quello che sappiamo succedere nella fisica reale del processo: quando immettiamo più energia, è più probabile che si passi da una fusione per conduzione (più superficiale) a una modalità con keyhole (penetrazione profonda), che appunto aumenta l’assorbimento e la profondità effettiva dell’interazione laser-materiale.

Usare valori costanti e non adattati, invece, può portare a errori enormi! Nel range di parametri che abbiamo studiato, abbiamo visto che l’errore nel predire le dimensioni della traccia fusa poteva arrivare fino al 194% rispetto al valore reale. Il nostro approccio permette di mitigare drasticamente questi errori.

Perché è Importante? Verso una Stampa 3D Migliore

Questo lavoro, secondo me, è un passo avanti significativo. Dimostra che è possibile migliorare notevolmente l’accuratezza delle simulazioni termiche PBF-LB senza dover ricorrere ai complessissimi e costosissimi modelli fluidodinamici completi. Basta rendere un po’ più “smart” il modo in cui modelliamo la sorgente laser, adattandone i parametri in base ai dati sperimentali.

Il metodo che abbiamo sviluppato è generale e potenzialmente trasferibile ad altri materiali e altri range di parametri. Questo apre la porta a simulazioni più efficienti dal punto di vista computazionale, ma comunque affidabili, che possono essere usate per:

• Comprendere meglio le dinamiche del processo.
• Ottimizzare i parametri di stampa per ridurre difetti come stress residui o porosità.
• Prevedere e controllare la microstruttura del materiale finale.
• Accelerare lo sviluppo di nuovi materiali e applicazioni per la PBF-LB.

Insomma, abbiamo trovato un modo per rendere le nostre “lenti virtuali” sul processo PBF-LB molto più nitide, aiutandoci a spingere sempre più in là i confini di questa tecnologia affascinante!

Fonte: Springer