Svelare i Segreti dei Modelli AI: Come Ricostruiamo i Dati Nascosti!

Ciao a tutti! Oggi voglio parlarvi di qualcosa che mi affascina tantissimo nel mondo del machine learning: la possibilità di “sbirciare” dentro un modello addestrato per cercare di recuperare i dati originali su cui ha imparato. Sembra fantascienza, vero? Eppure, è un campo di ricerca attivissimo, noto come ricostruzione dati tramite stima inversa e inferenza bayesiana.

Perché è così importante poter ricostruire i dati?

Pensateci un attimo. Viviamo in un’era dove i dati sono ovunque, ma spesso non sono accessibili direttamente. Prendiamo il federated learning, dove i modelli vengono addestrati su dati locali (ad esempio, sul vostro smartphone) senza che i dati grezzi lascino mai il dispositivo. Oppure il transfer learning, dove usiamo modelli pre-addestrati su dataset enormi che non possediamo. In questi scenari, poter ricostruire, anche solo parzialmente, i dati di addestramento partendo unicamente dal modello finale è una capacità potentissima.

Ma non solo! La ricostruzione dati ci aiuta a:

• Validare i modelli in modo più approfondito: possiamo scovare bias, anomalie o punti deboli che le metriche di performance classiche non rivelano.
• Capire meglio gli errori del modello: perché ha sbagliato una certa previsione? Forse i dati ricostruiti ci danno un indizio.
• Generare dati sintetici: inferire campioni simili ai dati reali è un passo fondamentale per creare dataset artificiali realistici, utili quando i dati originali sono scarsi o troppo sensibili per essere condivisi.

Il problema inverso nel Machine Learning

Questo processo di ricostruzione è, in sostanza, un problema inverso. Normalmente, nel machine learning, abbiamo un input (i dati) e vogliamo che il modello ci dia un output (una previsione, una classificazione). Questo è il problema “diretto”. Il problema inverso fa il contrario: conosciamo l’output desiderato (una certa classe, ad esempio) e vogliamo scoprire quali input (i dati originali) avrebbero portato il modello a produrre quell’output.

È un po’ come nella biologia dei sistemi, dove i ricercatori cercano di capire i meccanismi interni di una cellula (parametri non osservabili) partendo dai fenomeni che possono misurare all’esterno. Noi applichiamo un’idea simile ai modelli di machine learning.

Nel nostro studio, ci siamo concentrati su modelli addestrati su dati normalizzati con lo z-score. È una pratica comune che porta tutte le feature (le caratteristiche dei dati) su una scala simile, cosa che aiuta molti algoritmi, specialmente quelli basati su distanze o ottimizzazione a gradiente.

L’approccio Bayesiano: unire conoscenza pregressa e osservazioni

Per affrontare questa sfida, abbiamo scelto la strada dell’inferenza bayesiana. È un framework matematico elegantissimo che ci permette di aggiornare le nostre “credenze” (la distribuzione prior) sui parametri dei dati originali ((varvec{Theta })) man mano che osserviamo l’output del modello (la classe (c)).

In pratica, usiamo il teorema di Bayes per combinare:

• La distribuzione prior (q(varvec{Theta })): cosa pensiamo dei dati prima di guardare il modello.
• La funzione di verosimiglianza (likelihood) (p(c | varvec{Theta })): quanto è probabile osservare la classe (c) dati certi parametri (varvec{Theta }), secondo il modello.

Il risultato è la distribuzione posterior (q(varvec{Theta } mid c)): la nostra conoscenza aggiornata sui parametri dei dati, dopo aver considerato l’output del modello per quella classe.

Un nuovo framework teorico (e cosa ci dice)

Abbiamo sviluppato un nuovo framework teorico per capire meglio cosa influenza la qualità della ricostruzione. Usando un approccio basato sulle derivate parziali, abbiamo cercato di capire come piccole variazioni nelle variabili chiave impattano il risultato finale. La teoria ci suggerisce due fattori principali che governano la fedeltà dei dati recuperati:

1. L’accuratezza del prior assunto: quanto le nostre ipotesi iniziali sui dati (la distribuzione prior) si avvicinano alla realtà.
2. L’accuratezza del modello di machine learning: quanto bene il modello ha imparato dai dati originali.

In parole povere: se partiamo da ipotesi sbagliate sui dati o se il modello che stiamo “interrogando” non è molto accurato, la nostra ricostruzione sarà meno fedele. Sembra intuitivo, ma formalizzarlo matematicamente ci apre nuove strade per studiare i problemi inversi nel machine learning.

Certo, i nostri modelli teorici sono idealizzati, non catturano ogni sfumatura della pratica. Ma ci hanno guidato nel definire gli esperimenti per validare queste idee su dataset reali.

Mettere alla prova la teoria: esperimenti e risultati

Qui viene il bello! Avendo accesso ai dataset originali, possiamo calcolare le vere distribuzioni prior e posterior “marginali” (cioè, per ogni singola feature/parametro (theta_i)). Il prior vero (p(theta_i)) è semplicemente la distribuzione di quella feature sull’intero dataset. Il posterior vero (p(theta_i mid c)) è la distribuzione della stessa feature, ma calcolata solo sui dati appartenenti a una specifica classe (c). Avere questo “ground truth” è un lusso che ci permette di valutare quanto le nostre stime si avvicinano alla realtà.

Come prior assunto (q(theta_i)), abbiamo scelto una distribuzione uniforme nell’intervallo [-3, 3] per ogni parametro. Perché [-3, 3]? Perché lavorando con dati normalizzati (z-score), quasi tutti i valori (circa il 99.7%) cadono entro 3 deviazioni standard dalla media (che è 0). È una scelta semplice, un po’ come facevano i pionieri della statistica bayesiana come Bayes e Laplace quando non avevano informazioni specifiche a priori. È importante notare che i prior veri possono avere forme molto diverse (unimodali, bimodali, ecc.), non necessariamente uniformi o gaussiane.

La likelihood (p(c mid varvec{Theta })) l’abbiamo ottenuta direttamente dai modelli addestrati, usando la funzione `predict_proba` disponibile in librerie come scikit-learn, che ci dà la probabilità di ogni classe dati certi input (varvec{Theta }).

Abbiamo condotto esperimenti su diversi dataset benchmark (malattie cardiache, cancro al seno, riconoscimento cifre scritte a mano, ecc.) e con vari algoritmi di machine learning (reti neurali profonde, alberi decisionali, SVM, Naive Bayes, ecc.).

I risultati empirici hanno confermato le nostre aspettative teoriche! Abbiamo osservato correlazioni molto forti tra:

• La discrepanza tra prior vero e assunto (misurata con la divergenza di Kullback-Leibler, KLD) e la discrepanza tra posterior vero e stimato (KLD). Più il prior è accurato, migliore è la stima del posterior.
• L’errore di predizione del modello e la discrepanza tra posterior vero e stimato (KLD). Più il modello è accurato, migliore è la stima del posterior.

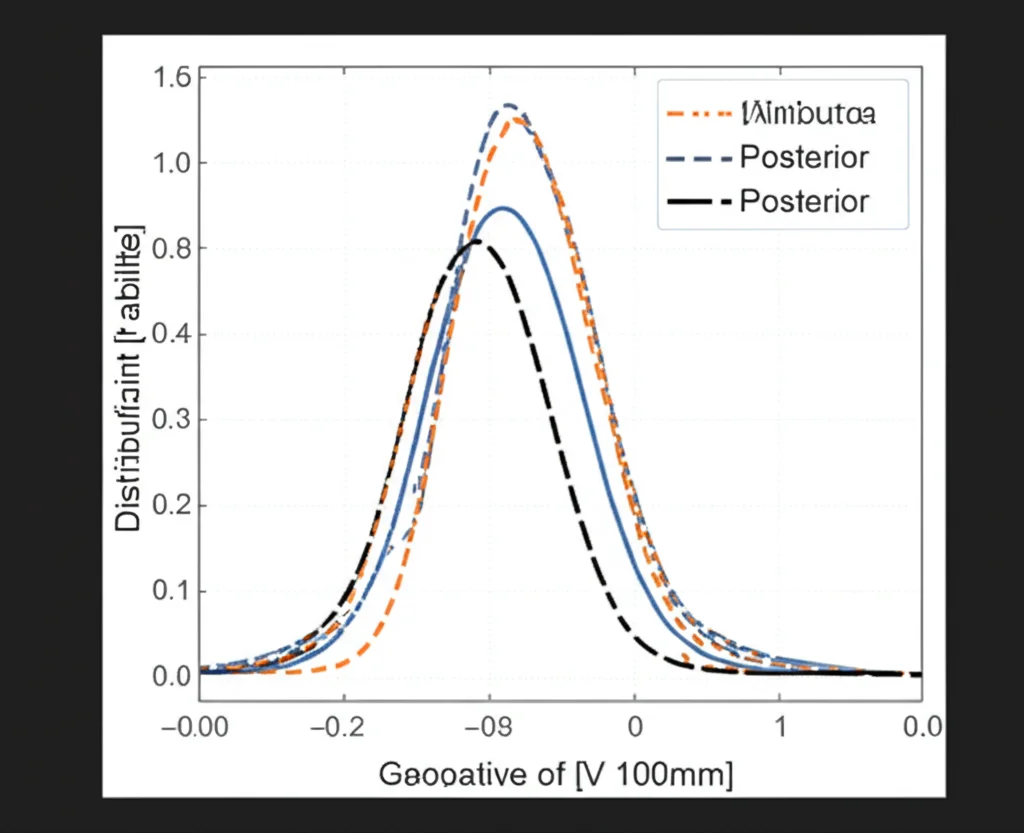
Queste correlazioni, spesso con coefficienti di Pearson superiori a 0.7 (considerati molto forti), sono emerse consistentemente attraverso diversi dataset e algoritmi.

L’esperimento “perfetto” e i modelli sintetici

Per spingere la validazione al limite, abbiamo fatto un esperimento usando i prior veri come prior assunti nel nostro processo di inferenza bayesiana, su un modello addestrato fino a raggiungere un’accuratezza perfetta (1.0) sul training set. Come previsto dalla teoria, i posterior stimati in questo scenario “ideale” erano incredibilmente vicini ai posterior veri, con valori di KLD bassissimi. Questo rafforza l’idea che se conosciamo perfettamente i prior e abbiamo un modello perfetto, la ricostruzione può essere estremamente accurata.

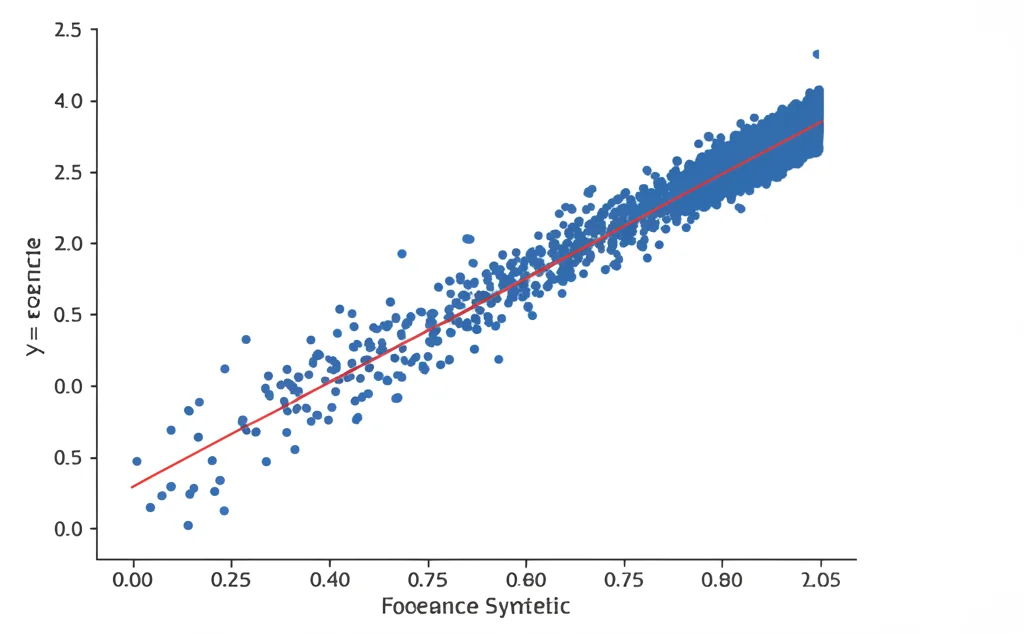
Un’altra scoperta interessante riguarda i modelli sintetici. Abbiamo preso i dati ricostruiti (i nostri “dataset sintetici”) e li abbiamo usati per addestrare nuovi modelli, usando lo stesso algoritmo e iperparametri dei modelli originali (“base”). Ebbene, abbiamo trovato una correlazione molto forte tra l’accuratezza dei modelli base e quella dei modelli sintetici, sia sul training set che, cosa più importante, sul test set originale. Non solo le accuratezze erano correlate, ma erano anche comparabili in termini assoluti! Questo significa che il nostro metodo di ricostruzione permette di creare modelli sintetici che replicano fedelmente le performance dei modelli originali. A volte, abbiamo persino notato che i modelli sintetici superavano leggermente quelli base sul test set!

Cosa significa tutto questo in pratica?

Questi risultati hanno implicazioni importanti.

L’importanza dei prior: La forte correlazione tra l’accuratezza del prior e la qualità della ricostruzione sottolinea quanto sia cruciale scegliere (o stimare) buoni prior. Anche se noi abbiamo usato prior uniformi per semplicità, in applicazioni reali bisognerebbe usare prior più informati, magari basati sulla conoscenza del dominio o su tecniche come Empirical Bayes o prior gerarchici, specialmente se i dati hanno strutture particolari (serie temporali, grafi).

L’importanza dell’accuratezza del modello: Allo stesso modo, l’accuratezza del modello è fondamentale. Errori nel modello si traducono direttamente in errori nella ricostruzione. Questo ci ricorda l’importanza di bilanciare bias e varianza (underfitting vs overfitting). Tecniche come la regolarizzazione (dropout, weight decay), la data augmentation, l’uso di ensemble (Random Forest, XGBoost) e la cross-validation sono essenziali non solo per migliorare le predizioni, ma anche per ottenere ricostruzioni dati più affidabili.

Gestire l’incertezza: Il nostro framework analizza come le incertezze nei prior e nel modello si propagano e influenzano la ricostruzione (quantificata dal KLD del posterior). Questo apre la porta all’uso di tecniche di quantificazione dell’incertezza più avanzate in futuro.

Creare modelli sintetici efficaci: La capacità di generare modelli sintetici con performance paragonabili agli originali è forse uno dei risultati più pratici. Potrebbe permettere la condivisione di “modelli proxy” senza condividere i dati sensibili originali.

Come abbiamo fatto? (Un pizzico di metodologia)

Per stimare le distribuzioni posterior, abbiamo usato un metodo di campionamento chiamato Markov Chain Monte Carlo (MCMC), specificamente l’algoritmo di Metropolis. Immaginate un “esploratore” che si muove nello spazio dei possibili parametri dei dati. Ad ogni passo, propone un nuovo set di parametri e decide se accettarlo o meno basandosi su quanto quel set sia “plausibile” secondo il modello di machine learning (usando la likelihood). Dopo molti passi (nel nostro caso, 5000 campioni accettati per classe), l’insieme dei punti visitati dall’esploratore ci dà un’approssimazione della distribuzione posterior.

Per creare i modelli base con diversi livelli di accuratezza, abbiamo sistematicamente “distorto” i dati di training originali, applicando piccoli shift ai valori delle feature, e poi addestrando un modello su ciascuna versione distorta.

In conclusione

Il nostro lavoro getta nuova luce sulla sfida affascinante della ricostruzione dei dati dai modelli di machine learning. Abbiamo fornito un framework teorico che spiega i fattori chiave in gioco e l’abbiamo validato con esperimenti rigorosi. Abbiamo dimostrato che l’accuratezza dei prior e del modello sono cruciali e che è possibile creare modelli sintetici che mimano efficacemente gli originali. Spero che questo viaggio nella “scienza inversa” del machine learning vi abbia incuriosito almeno quanto ha appassionato me! È un campo con enormi potenzialità, sia per capire meglio i nostri modelli AI, sia per sviluppare nuove applicazioni pratiche.

Fonte: Springer