L’Ordine Nascosto delle Matrici: Svelando i Segreti del ‘Sharp Partial Order’

Ciao a tutti, appassionati di matematica e curiosi! Oggi voglio portarvi con me in un viaggio affascinante nel mondo apparentemente astratto, ma incredibilmente strutturato, delle matrici complesse. Non spaventatevi, non parleremo di cose astruse fini a sé stesse. Esploreremo insieme un concetto chiamato “ordine parziale sharp” (sì, lo so, suona un po’ tecnico, ma datemi fiducia!) e scopriremo come ci permette di “mettere in ordine” certe matrici speciali, quelle che hanno un “indice al più 1”. Pensate a come mettiamo in ordine i numeri (2 è minore di 5) o le parole in un dizionario. Ecco, qui facciamo qualcosa di simile, ma con oggetti matematici più complessi: le matrici.

Cos’è questo “Ordine Parziale Sharp”?

Immaginate di avere due matrici, A e B, appartenenti a questa classe speciale ( {mathbb {C}}_1^n ) (matrici quadrate complesse (n times n) con indice al più 1, il che significa, in soldoni, che hanno una particolare inversa chiamata “inversa di gruppo”, denotata con (A^sharp)). Diciamo che A è “minore o uguale” a B secondo l’ordine sharp, e scriviamo (A {mathop {le }limits ^{_{sharp }}}B ), se succedono due cose carine: ( A^sharp A= A^sharp B) e (AA^sharp = BA^sharp ). Un modo forse più intuitivo, anche se equivalente, è dire che (A^2=AB=BA). Sembra una definizione un po’ strana, vero? Eppure, definisce un modo rigoroso per confrontare queste matrici.

Il nostro obiettivo oggi è capire che tipo di “struttura” emerge quando guardiamo a tutte le matrici A che sono “sotto” una certa matrice B fissata, secondo questo ordine sharp. Questo insieme, che chiamiamo “down-set” e indichiamo con ([O, B]) (dove O è la matrice nulla, l’elemento più piccolo), ha delle proprietà nascoste molto interessanti, in particolare le sue “proprietà reticolari”. Cosa significa “reticolare”? Beh, in parole povere, ci chiediamo se, prendendo due matrici (A_1) e (A_2) in ([O, B]), possiamo sempre trovare un’unica matrice che sia il loro “massimo predecessore comune” (l’infimo, (A_1 wedge A_2)) e un’unica matrice che sia il loro “minimo successore comune” (il supremo, (A_1 vee A_2)) all’interno di ([O, B]). Se la risposta è sì per ogni coppia, allora ([O, B]) è un reticolo.

Semplificare con la Magia degli Isomorfismi

Studiare direttamente l’insieme ([O, B]) può essere complicato. Le matrici possono essere grandi e maneggiarle non è sempre facile. Qui entra in gioco la bellezza della matematica: possiamo trovare delle “mappe magiche”, chiamate isomorfismi, che trasformano il nostro problema in uno equivalente, ma molto più semplice da analizzare!

Il primo passo è usare una scomposizione speciale della matrice B, chiamata decomposizione di Hartwig-Spindelböck. Non entriamo nei dettagli tecnici, ma questa scomposizione ci permette di associare a ogni matrice (A in [O, B]) una matrice (T) molto più piccola (di dimensione (r times r), dove (r) è il rango di B) che ha due proprietà fondamentali: è un proiettore (cioè (T^2 = T)) e “commuta” con una parte specifica della decomposizione di B (una matrice che chiamiamo (Sigma K), dove K deve essere non singolare perché (B in {mathbb {C}}_1^n)). L’insieme di tutti questi proiettori T, che chiamiamo (tau), ha una sua struttura d’ordine (diciamo (T_1 le T_2) se (T_1 = T_1 T_2 = T_2 T_1)). La cosa fantastica è che l’insieme originale ([O, B]) e questo nuovo insieme (tau) sono isomorfi: si comportano esattamente allo stesso modo rispetto all’ordine! Lavorare con i proiettori in (tau) è già un bel vantaggio.

Ma non ci fermiamo qui! Possiamo fare un ulteriore passo di semplificazione. La matrice (Sigma K) può essere trasformata nella sua forma canonica di Jordan, J, tramite una matrice invertibile P ((Sigma K = PJP^{-1})). La forma di Jordan è come la “carta d’identità” di una matrice, rivela la sua struttura più profonda legata agli autovalori e ai blocchi di Jordan. Ebbene, scopriamo un altro isomorfismo! L’insieme (tau) è isomorfo a un nuovo insieme, (delta), che contiene i proiettori che commutano direttamente con la forma di Jordan J! Questo è potentissimo, perché la struttura di J è ben nota e studiarla ci dà informazioni dirette sulle proprietà reticolari di (delta), e quindi, a ritroso, di (tau) e del nostro ([O, B]) originale.

La Risposta Chiave: Quando [O, B] è un Reticolo?

Grazie a questo secondo isomorfismo e all’analisi dei proiettori che commutano con la forma di Jordan J, arriviamo al cuore della questione. Quando ([O, B]) è un reticolo? La risposta è sorprendentemente precisa:

[O, B] è un reticolo se e solo se la molteplicità geometrica di ogni autovalore della matrice (Sigma K) è al massimo 2.

Cosa significa “molteplicità geometrica”? È il numero di blocchi di Jordan associati a un certo autovalore nella forma canonica J. Quindi:

• Se ogni autovalore ha un solo blocco di Jordan (molteplicità geometrica 1), allora ([O, B]) non solo è un reticolo, ma è una struttura ancora più “bella”: un’algebra Booleana. Pensate a una struttura logica con operazioni AND, OR, NOT.
• Se qualche autovalore ha due blocchi di Jordan (molteplicità geometrica 2), ([O, B]) è ancora un reticolo, ma la sua struttura è più complessa (non è più distributivo, contiene delle sotto-strutture particolari).
• Se anche un solo autovalore ha tre o più blocchi di Jordan (molteplicità geometrica ≥ 3), la struttura si “rompe”: ([O, B]) non è più un reticolo! Non possiamo più garantire l’esistenza unica dell’infimo o del supremo per tutte le coppie.

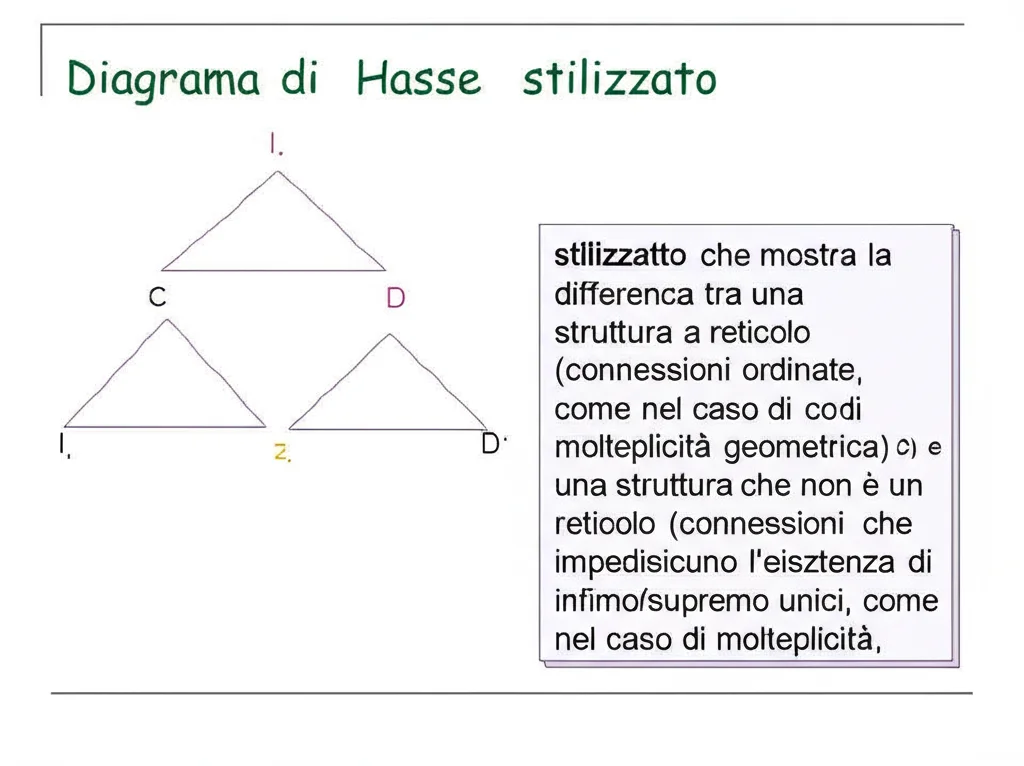= 3). Obiettivo macro 60mm, alta definizione, illuminazione controllata per evidenziare la struttura.” />

Un Gioiello Nascosto: L’Algebra Booleana Interna

Anche quando ([O, B]) non è un’algebra Booleana completa (ad esempio, se ci sono autovalori con molteplicità 2), scopriamo che c’è sempre un’algebra Booleana “nascosta” al suo interno! Si tratta dell’insieme ({mathcal {C}}) dei proiettori in (tau) che commutano con tutti gli altri proiettori in (tau). Grazie all’isomorfismo con (delta), possiamo descrivere precisamente gli elementi di questa algebra: corrispondono ai proiettori in (delta) che sono diagonali a blocchi, dove ogni blocco diagonale corrispondente a un autovalore (lambda_j) è o la matrice identità (I_{r_j}) o la matrice nulla O. Il numero di elementi in questa algebra Booleana è (2^s), dove (s) è il numero di autovalori distinti di (Sigma K).

Guardando Oltre: L’Intero Insieme ({mathbb {C}}_1^n) e Altre Scoperte

Il nostro studio non si limita al “down-set” ([O, B]). Abbiamo anche esaminato l’intera “popolazione” di matrici ({mathbb {C}}_1^n) con l’ordine sharp. Un risultato importante, dimostrato da Mitra negli anni ’80, diceva che per (n ge 4), questo insieme non è un “semireticolo inferiore” (cioè, non sempre esiste l’infimo tra due matrici qualsiasi). Noi abbiamo esteso questo risultato: abbiamo dimostrato che questo vale anche per (n=3)! Quindi, l’insieme ({mathbb {C}}_1^n) si comporta “bene” (è un semireticolo inferiore) solo per dimensioni molto piccole: (n le 2). Per (n ge 3), l’ordine sharp sull’intero insieme inizia a mostrare delle “crepe” strutturali.

Inoltre, abbiamo affrontato una congettura proposta da Mitra e colleghi riguardo alla caratterizzazione delle matrici (A le_sharp B) usando la decomposizione di Jordan di B. Abbiamo mostrato, con un controesempio, che la congettura non è vera così com’è stata formulata. Tuttavia, abbiamo fornito un risultato corretto che caratterizza le matrici B che stanno “sopra” una data matrice A, sempre usando la decomposizione di Jordan, ma quella di A questa volta.

A Cosa Serve Tutto Questo? Applicazioni!

Potreste chiedervi: “Ok, affascinante, ma a che serve?”. Beh, queste scoperte sulla struttura dell’ordine sharp e gli isomorfismi con gli insiemi di proiettori hanno applicazioni concrete. Ad esempio, ci permettono di caratterizzare le soluzioni di certi sistemi di equazioni matriciali. Immaginate di cercare una matrice X che sia un proiettore ((X^2=X)) e che commuti con una data matrice B ((BX=XB)). Grazie ai nostri isomorfismi, possiamo trovare tutte le soluzioni X descrivendole in termini dei proiettori T negli insiemi (tau) o (delta), che sono molto più facili da gestire! Questo è particolarmente utile quando B ha certe proprietà (come essere EP o avere una forma di Jordan semplice).

Conclusione

Il nostro viaggio nell’ordine parziale sharp ci ha mostrato come, anche in strutture matematiche apparentemente complesse, possiamo trovare ordine e regolarità, ma anche punti in cui questa regolarità si spezza. L’uso intelligente degli isomorfismi ci ha permesso di “tradurre” un problema difficile in linguaggi più semplici (quello dei proiettori che commutano con (Sigma K) o con la sua forma di Jordan J), rivelando le condizioni precise sotto cui l’insieme ([O, B]) forma un reticolo. Abbiamo anche visto come queste idee si estendono all’intero insieme ({mathbb {C}}_1^n) e trovano applicazione nella soluzione di equazioni matriciali. Spero che questa esplorazione vi abbia incuriosito e mostrato un piccolo angolo dell’eleganza e della profondità nascoste nel mondo dell’algebra lineare!

Fonte: Springer