Ancore nel Terreno: Sveliamo la Loro Forza con le Reti di Kolmogorov-Arnold (KAN)!

Ciao a tutti! Oggi voglio parlarvi di qualcosa che sta cambiando il modo in cui guardiamo… sotto terra! Avete presente le grandi strutture come torri di trasmissione, piattaforme offshore o muri di contenimento? Bene, spesso la loro stabilità dipende da elementi chiamati ancore, infissi nel terreno per resistere a forze di sollevamento. Capire esattamente quanta forza queste ancore possano sopportare è cruciale, ma non è affatto semplice, specialmente in terreni complessi, quelli che chiamiamo “attrito-coesivi” (un mix di sabbia e argilla, per intenderci).

Per decenni ci siamo affidati a esperimenti e formule empiriche, ma avevano i loro limiti. Ora, però, abbiamo nuovi strumenti potentissimi che vengono dal mondo dell’intelligenza artificiale. In particolare, uno studio recente ha esplorato l’uso delle Reti di Kolmogorov-Arnold (KAN) per prevedere la capacità di sollevamento di ancore circolari. E lasciate che ve lo dica, i risultati sono davvero promettenti!

Il Cuore del Problema: Capire i Fattori di Stabilità

Quando un’ancora viene tirata verso l’alto, il terreno circostante si oppone. Questa resistenza, chiamata capacità di sollevamento (Pu), dipende da un sacco di cose:

• Le proprietà del terreno: la sua coesione (quanto le particelle stanno “appiccicate” tra loro, c), l’angolo di attrito interno (quanto le particelle resistono allo scorrimento reciproco, φ) e il suo peso specifico (γ).
• La geometria dell’ancora: in particolare il rapporto tra la profondità di infissione (H) e il diametro dell’ancora (D), cioè H/D.
• Eventuali carichi aggiuntivi sulla superficie del terreno (il cosiddetto sovraccarico, q).
• La “rugosità” dell’interfaccia tra ancora e terreno (R), che ci dice quanto attrito c’è tra i due.

Per semplificare, si usa un approccio simile a quello del grande Terzaghi per le fondazioni: si scompone la capacità totale in tre contributi, ognuno legato a un “fattore di stabilità”:

• Fc: legato alla coesione del terreno.
• Fq: legato al sovraccarico.
• Fγ: legato al peso del terreno stesso.

La formula diventa: Pu = c * Fc + q * Fq + γ * D * Fγ (semplificata per chiarezza). Il trucco sta nel calcolare questi tre fattori (Fc, Fq, Fγ) in modo accurato, perché dipendono in modo complesso da H/D e φ.

I Metodi Tradizionali e i Loro Limiti

In passato, si usavano test fisici o formule basate su ipotesi semplificate sui meccanismi di rottura del terreno. Poi sono arrivate le analisi numeriche, come il Metodo degli Elementi Finiti (FEM), che hanno permesso simulazioni più realistiche. Tuttavia, molte analisi erano bidimensionali (plane strain), che non catturano appieno il comportamento tridimensionale delle ancore circolari.

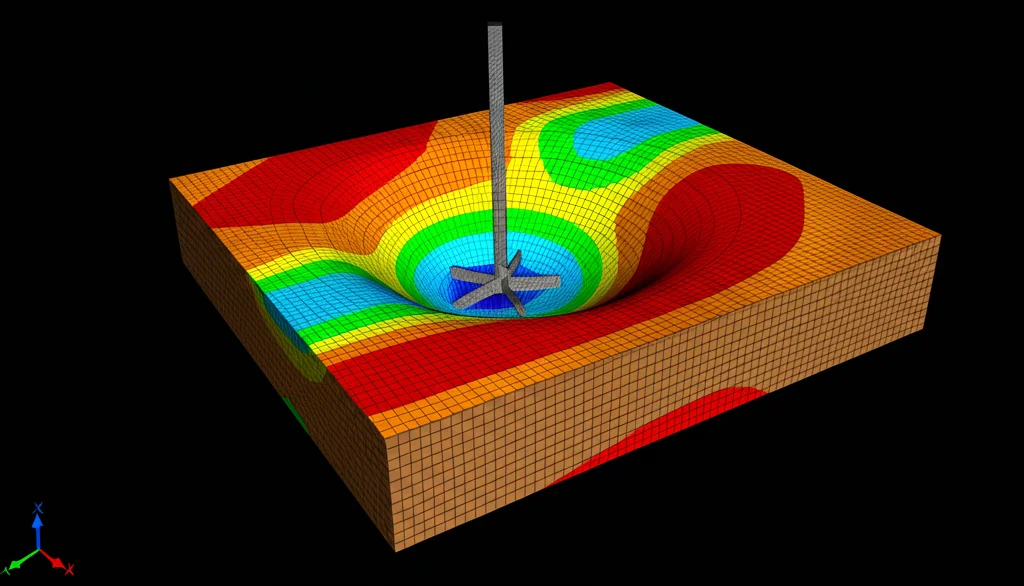
Studi recenti hanno iniziato a usare tecniche più avanzate come l’Analisi Limite agli Elementi Finiti (FELA), che permette di calcolare limiti superiori (UB) e inferiori (LB) della capacità portante, dandoci un intervallo di valori affidabili. Questo studio ha usato proprio FELA con una tecnica chiamata “adaptive meshing”, che infittisce la “griglia” di calcolo dove serve (vicino all’ancora, dove il terreno si deforma di più), per ottenere risultati ancora più precisi.

La Rivoluzione KAN: Intelligenza Artificiale che “Spiega”

Qui entra in gioco la vera novità: le Reti di Kolmogorov-Arnold (KAN). Molti conoscono le Reti Neurali Artificiali (ANN), usate tantissimo nel machine learning. Le ANN sono potenti, ma spesso sono delle “scatole nere”: funzionano bene, ma è difficile capire *perché* danno un certo risultato.

Le KAN, basate su un teorema matematico affascinante (il teorema di rappresentazione di Kolmogorov-Arnold), sono diverse. Invece di avere funzioni di attivazione fisse *dentro* i nodi (come le ANN), le KAN hanno funzioni di attivazione *sugli archi* (le connessioni tra nodi), e queste funzioni sono “apprendibili”, cioè si adattano ai dati! Usano delle funzioni matematiche chiamate “spline”.

Questo approccio ha vantaggi enormi:

• Meno parametri: Richiedono meno “manopole” da regolare rispetto alle ANN per ottenere la stessa precisione.
• Minore overfitting: Rischiano meno di “imparare a memoria” i dati di training e funzionare male su dati nuovi.
• Maggiore interpretabilità: È più facile capire come ogni variabile di input influenza l’output. Si possono visualizzare le funzioni apprese sugli archi!
• Formule esplicite: È possibile estrarre dalle KAN addestrate delle vere e proprie formule matematiche (anche se complesse!) per calcolare i fattori di stabilità.

Questo studio è il primo ad applicare le KAN al comportamento delle ancore, e i risultati sono stati strabilianti.

Come Hanno Fatto: La Metodologia in 5 Passi

Il team di ricerca ha seguito un percorso logico:

1. Hanno eseguito tantissime simulazioni FELA (sia Upper Bound che Lower Bound) per diverse combinazioni di H/D, φ e R, calcolando i valori di Fc, Fq e Fγ.
2. Hanno creato un grande dataset con tutti questi risultati (input: H/D, φ, R; output: Fc, Fq, Fγ).
3. Hanno addestrato modelli KAN su questi dati per catturare le relazioni non lineari tra input e output.
4. Hanno derivato delle formule matematiche esplicite (closed-form) per Fc, Fq e Fγ direttamente dai modelli KAN.
5. Hanno interpretato i risultati per trarre conclusioni utili per la progettazione ingegneristica.

Cosa Abbiamo Imparato: I Risultati Chiave

L’analisi ha rivelato cose molto interessanti sul comportamento dei fattori di stabilità:

* Fattore di Coesione (Fc): Aumenta significativamente all’aumentare sia di H/D che di φ. Più l’ancora è profonda e più il terreno ha attrito, maggiore è il contributo della coesione. La rugosità (R) ha un impatto quasi nullo su Fc. I meccanismi di rottura diventano più complessi e curvi (non lineari) man mano che H/D aumenta.
* Fattore di Sovraccarico (Fq): Anche Fq cresce molto con H/D e φ. L’effetto del sovraccarico è minimo per terreni puramente coesivi (φ=0) ma diventa importantissimo in terreni con attrito, specialmente a grandi profondità. Anche qui, la rugosità R è ininfluente. La non linearità del meccanismo di rottura è ancora più marcata per Fq a grandi H/D.
* Fattore di Peso Unitario (Fγ): Simile agli altri, Fγ aumenta con H/D e φ. L’effetto di φ è particolarmente forte a grandi profondità. La rugosità R continua ad avere un impatto trascurabile. Il meccanismo di rottura diventa più ampio con H/D, ma la non linearità sembra leggermente meno accentuata rispetto a Fc e Fq.

Quando i ricercatori hanno confrontato i loro risultati FELA con studi precedenti, hanno trovato un buon accordo generale per Fc e Fγ, rafforzando la validità delle simulazioni. Per Fq, c’erano meno dati di confronto e alcune discrepanze con teorie più vecchie (come quella di Meyerhof), specialmente a basse profondità, ma la vicinanza tra i risultati Upper Bound e Lower Bound ottenuti con FELA dava grande fiducia nei nuovi valori.

KAN vs ANN: La Sfida Vinta

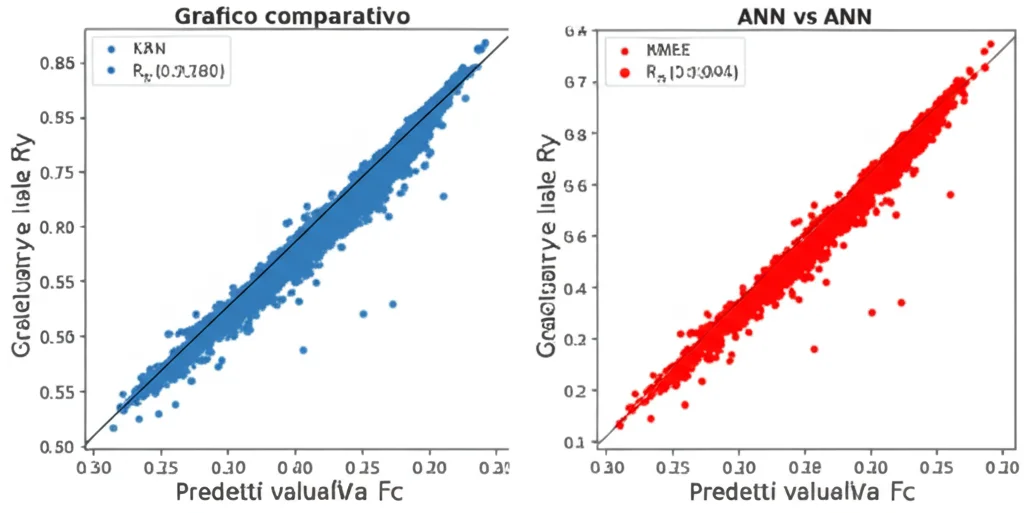
La parte più eccitante è stata confrontare le prestazioni dei modelli KAN con quelle di reti neurali tradizionali (ANN) addestrate sugli stessi dati. I risultati sono stati netti:

• I modelli KAN hanno raggiunto coefficienti di determinazione (R²) praticamente perfetti (1.000 o 0.999) sia sui dati di training che di test per tutti e tre i fattori. Le ANN, pur buone (R² tra 0.986 e 0.999), erano leggermente inferiori.
• Gli errori (RMSE e MAE) dei modelli KAN erano significativamente più bassi di quelli delle ANN, a volte anche 3-4 volte inferiori sui dati di test.
• Le KAN hanno mostrato una migliore capacità di generalizzazione (performance su dati mai visti prima).

In pratica, le KAN non solo erano più accurate, ma anche più affidabili.

Capire Cosa Conta Davvero: SHAP e PDP

Grazie all’interpretabilità delle KAN, è stato possibile usare tecniche come SHAP (SHapley Additive exPlanations) e PDP (Partial Dependence Plots) per capire *quanto* ogni parametro di input influenzasse i risultati.

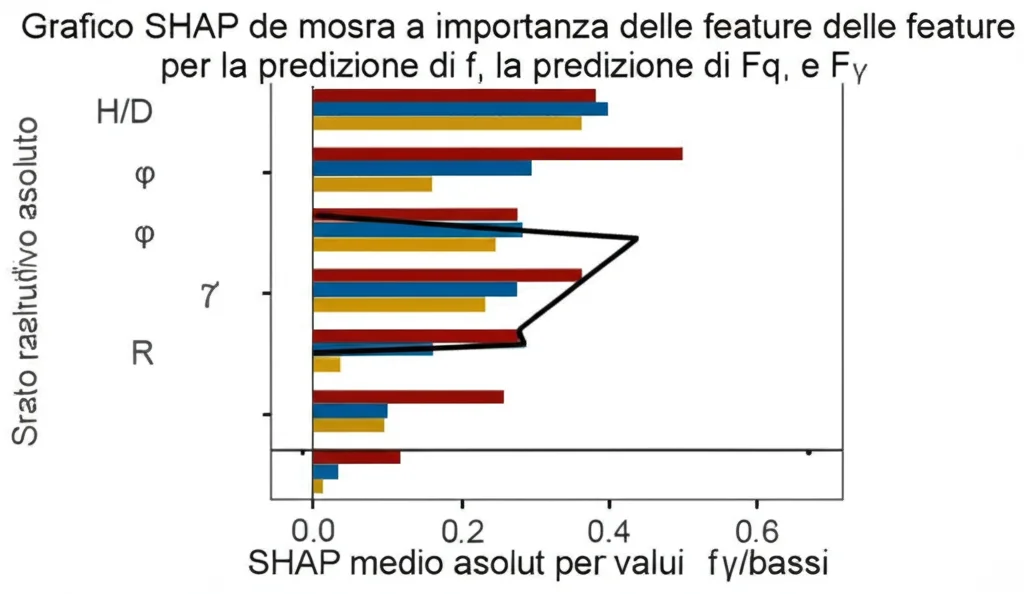
L’analisi SHAP ha confermato che:

• H/D (Profondità/Diametro) è molto influente, specialmente per Fc, ma il suo impatto relativo diminuisce leggermente per Fγ.
• φ (Angolo d’attrito) è costantemente importante per tutti e tre i fattori, diventando relativamente più cruciale per Fγ.
• R (Rugosità) ha un’influenza praticamente nulla su tutti e tre i fattori!

Quest’ultimo punto è fondamentale per la pratica: significa che piccole variazioni nella rugosità dell’ancora (dovute a produzione o installazione) probabilmente non cambiano molto la sua capacità di sollevamento in questi terreni. Gli ingegneri possono quindi concentrarsi di più sull’ottimizzazione della profondità (H/D) e sulla caratterizzazione dell’angolo d’attrito (φ).

I grafici PDP hanno visualizzato queste dipendenze, mostrando chiaramente le curve (spesso fortemente non lineari) di come Fc, Fq e Fγ cambiano al variare di H/D e φ, e confermando la “piattezza” della risposta al variare di R.

Formule Pronte all’Uso (per Ingegneri Coraggiosi!)

Uno dei risultati più pratici dello studio è stata la derivazione di formule matematiche esplicite per Fc, Fq e Fγ basate sui modelli KAN ottimizzati. Queste formule, anche se appaiono molto complesse a prima vista (piene di seni, tangenti iperboliche, sigmoidi…), hanno un vantaggio incredibile: contengono solo operazioni aritmetiche di base.

Questo significa che possono essere implementate direttamente in un comune foglio di calcolo (come Excel)! Un ingegnere può inserire i valori specifici del progetto (H/D, φ) e ottenere istantaneamente una stima molto accurata dei fattori di stabilità, senza bisogno di software specializzati o complesse simulazioni FELA (che rimangono utili per analisi di dettaglio). Questo è un enorme passo avanti per la progettazione preliminare e concettuale.

Ecco le forme generali (le formule complete sono… lunghe!):

• Fc = funzione(H/D, φ)
• Fq = funzione(H/D, φ)
• Fγ = funzione(H/D, φ)

(Nota: Nelle formule derivate, la rugosità R appariva, ma la sua influenza era così piccola che le versioni semplificate qui sopra sono praticamente equivalenti e più utili).

Limiti e Prospettive Future

Come ogni studio, anche questo ha i suoi limiti. Si è concentrato su ancore circolari, in terreni omogenei (senza strati diversi), usando un modello di materiale semplice (Mohr-Coulomb) e condizioni assialsimmetriche. Non considera effetti come l’anisotropia del terreno o comportamenti dipendenti dal tempo.

Tuttavia, la bellezza dell’approccio FELA-KAN è la sua flessibilità. Potrebbe essere esteso in futuro per:

• Analizzare altri tipi di ancore (elicoidali, a gruppo…).
• Includere terreni stratificati o spazialmente variabili.
• Usare modelli di materiale più complessi.
• Considerare effetti tridimensionali più generali o carichi sismici.

In Conclusione: Un Nuovo Potente Alleato per la Geotecnica

Questo lavoro rappresenta un passo avanti significativo. Combinando la potenza delle simulazioni FELA con l’intelligenza e l’interpretabilità delle reti KAN, abbiamo ora strumenti migliori per prevedere la capacità di sollevamento delle ancore circolari.

I modelli KAN non solo superano le prestazioni delle ANN tradizionali, ma ci forniscono anche formule esplicite e facili da usare nei fogli di calcolo, rendendo queste tecniche avanzate accessibili per la pratica ingegneristica quotidiana. Inoltre, l’analisi di sensibilità ci ha confermato quali parametri contano davvero (profondità e attrito del terreno) e quali meno (la rugosità dell’ancora).

Insomma, le KAN si profilano come un alleato prezioso per progettare strutture più sicure ed efficienti, aiutandoci a capire meglio le complesse interazioni tra le nostre costruzioni e il terreno che le sostiene. Non vedo l’ora di vedere come questa tecnologia si evolverà e verrà applicata ad altri problemi geotecnici!

Fonte: Springer