Prevedere le Pandemie? Un Mix Geniale di Matematica e AI Ci Mostra Come!

Ciao a tutti! Oggi voglio parlarvi di qualcosa che mi appassiona tantissimo e che, come abbiamo visto tragicamente con il COVID-19, tocca le vite di tutti noi: come prevedere la diffusione delle malattie. Sembra fantascienza, vero? Eppure, la scienza fa passi da gigante, e voglio raccontarvi di un approccio nuovo, incredibilmente semplice ma efficace, che abbiamo sviluppato.

La Sfida: Capire il Caos delle Epidemie

Da tempo, noi scienziati usiamo modelli matematici, come il famoso modello SIR (Susceptible-Infected-Recovered), per cercare di capire come si propagano le infezioni. Immaginate di dividere la popolazione in gruppi – suscettibili, infetti, guariti – e usare equazioni per descrivere come le persone passano da un gruppo all’altro. Questi modelli sono stati fondamentali, ci hanno aiutato a stimare la durata di un’epidemia, il famoso R0 (il numero di riproduzione), e a guidare le decisioni di sanità pubblica.

Poi, abbiamo cercato di renderli più realistici. Abbiamo aggiunto lo stato “Esposto” (modello SEIR), per tener conto del periodo di incubazione. Abbiamo considerato le interazioni tra persone, come i contatti stretti che diffondono il virus a livello locale. E abbiamo capito che queste interazioni, su larga scala, portano alla diffusione tra regioni diverse, creando complessi pattern spazio-temporali. Pensate a come un focolaio in una città può viaggiare con le persone e accenderne altri altrove. Anche i processi di diffusione matematica sono stati usati per modellare questa dinamica.

Il problema? Più dettagli aggiungiamo, più i modelli diventano complessi. E indovinate un po’? Stimare i parametri giusti diventa un incubo, e a volte, paradossalmente, la precisione delle previsioni ne risente. Ironico, no? Cerchi di migliorare l’accuratezza e finisci per peggiorarla! Per questo, spesso si preferiscono ancora modelli più semplici, con le giuste assunzioni.

L’Intelligenza Artificiale Entra in Scena

Negli ultimi anni, però, è arrivato un nuovo giocatore potentissimo: il deep learning. Le reti neurali artificiali (ANN), le reti neurali ricorrenti (RNN) e le reti neurali su grafo (GNN) hanno mostrato capacità predittive sbalorditive in tantissimi campi, dalla finanza al riconoscimento vocale, fino all’analisi del traffico. E ovviamente, abbiamo iniziato a usarle anche per modellare la diffusione delle malattie.

Perché? Perché una maggiore potenza predittiva è utilissima! A livello nazionale, aiuta a ottimizzare campagne vaccinali o restrizioni alla mobilità. A livello regionale, supporta l’allocazione tempestiva di risorse e interventi mirati. Modelli che combinano RNN (per il tempo) e GNN (per lo spazio) hanno spesso superato i modelli matematici tradizionali in termini di accuratezza.

Ma c’è un “ma”. I modelli di deep learning sono spesso delle “scatole nere”. Funzionano benissimo, ma capire *perché* fanno una certa previsione è difficile. Perdiamo quella che chiamiamo interpretabilità, un grande pregio dei modelli matematici, che ci danno insight chiari sulle dinamiche di diffusione.

La Nostra Idea: Il Meglio dei Due Mondi

Ed è qui che entra in gioco la nostra idea. Ci siamo chiesti: possiamo creare un modello che abbia la potenza predittiva del deep learning *e* l’interpretabilità dei modelli matematici? Un modello che sia anche semplice da usare e i cui parametri siano facili da stimare?

La risposta è sì! Abbiamo proposto un modello ibrido che chiamiamo “diffusion-informed neural network” (rete neurale informata dalla diffusione). È incredibilmente semplice, ma funziona alla grande.

Come abbiamo fatto? Siamo partiti da un modello matematico di base che considera due cose principali:

1. La generazione di nuovi casi all’interno di una regione (simile ai modelli SIR).
2. La diffusione della malattia verso regioni adiacenti, tramite le reti di trasporto (auto, treno, aereo…).

Matematicamente, si può scrivere come un’equazione (la Eq. 1 nel paper originale) che lega l’aumento dei casi ((dX_t/dt)) ai casi accumulati attuali ((X_t)) e ai volumi di trasporto tra regioni ((A^k)), con dei coefficienti ((theta)) che rappresentano la “forza” della generazione locale e della diffusione tramite ogni mezzo di trasporto.

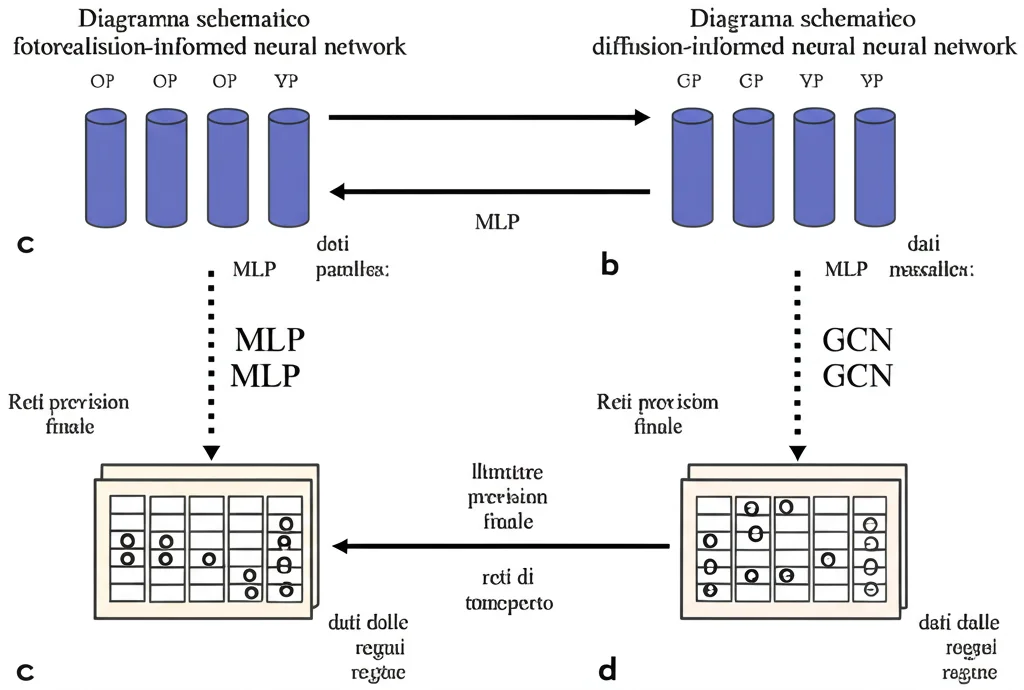
Poi, abbiamo “tradotto” questa idea matematica in un modello di rete neurale (Eq. 2 e Fig. 1 nel paper). E qui sta la bellezza: la struttura della rete neurale rispecchia direttamente quella matematica!

Come Funziona la Rete “Ibrida”?

Il nostro modello ha due “rami” che lavorano in parallelo:

• Ramo Generazione: Una semplice rete neurale artificiale (un Multi-Layer Perceptron, MLP) che guarda i dati di incidenza degli ultimi ‘m’ giorni in una regione ((widehat{X}_{t-m:t})) e stima quanti nuovi casi verranno generati *internamente*. Impara un parametro ((theta_g)) che corrisponde al coefficiente di generazione del modello matematico.
• Ramo Diffusione: Una rete neurale convoluzionale su grafo (GCN) modificata. Questa parte guarda come l’incidenza nelle regioni vicine, collegata tramite i volumi di trasporto ((A^k)), influenzi i nuovi casi nella regione considerata. Impara dei parametri ((theta_d^k)) per ogni mezzo di trasporto, simili ai coefficienti di diffusione matematici.

Infine, i risultati dei due rami vengono sommati per ottenere la previsione dei nuovi casi del giorno dopo ((widehat{X}_{t+1})).

Un dettaglio tecnico importante: invece di usare i casi *accumulati* (come farebbe un modello SIR puro, ma spesso non abbiamo quei dati), usiamo la *storia* recente dei casi giornalieri (gli ultimi ‘m’ giorni). È una tecnica comune nel deep learning per dati temporali, e con una finestra temporale (‘m’) abbastanza lunga, può approssimare l’informazione contenuta nei casi accumulati.

E il bello? Per trovare i parametri ottimali ((theta_g) e (theta_d^k)), usiamo tutta la potenza degli algoritmi di training del deep learning (come la retropropagazione dell’errore, ottimizzatori avanzati, ecc.). Questo rende la stima dei parametri molto più semplice e automatica rispetto ai metodi tradizionali, che spesso richiedono “indovinare” valori iniziali o aggiustamenti manuali, specialmente con dati rumorosi o complessi.

Alla Prova dei Fatti: Il COVID-19 in Spagna

Per vedere se il nostro modello funzionava davvero, lo abbiamo applicato ai dati giornalieri di incidenza del COVID-19 in 52 province spagnole, per un periodo di circa 15 mesi (gennaio 2020 – marzo 2021). Avevamo anche dati (pre-pandemia, del 2018) sui flussi medi di trasporto tra queste regioni (auto, pullman, treno, aereo, nave).

Abbiamo allenato il modello sui primi 350 giorni e lo abbiamo testato sugli ultimi 100. Abbiamo cercato i migliori iperparametri (come la lunghezza della finestra temporale ‘m’ e il numero di “canali” nella GCN) usando una parte dei dati di training come validazione. Alla fine, abbiamo scoperto che una finestra di 14 giorni e 16 canali GCN davano i risultati migliori. Curiosamente, 14 giorni è il doppio della periodicità settimanale che abbiamo notato nei dati (probabilmente dovuta a meno test nel weekend), il che si allinea col teorema di Nyquist sul campionamento dei segnali!

E i risultati? Strepitosi! Il nostro modello ha ottenuto una correlazione altissima (0.9679) tra le previsioni e i dati reali nel set di test. Ha previsto accuratamente sia l’andamento nazionale complessivo sia le variazioni regionali.

Confronto con Altri Modelli: Semplice è Meglio?

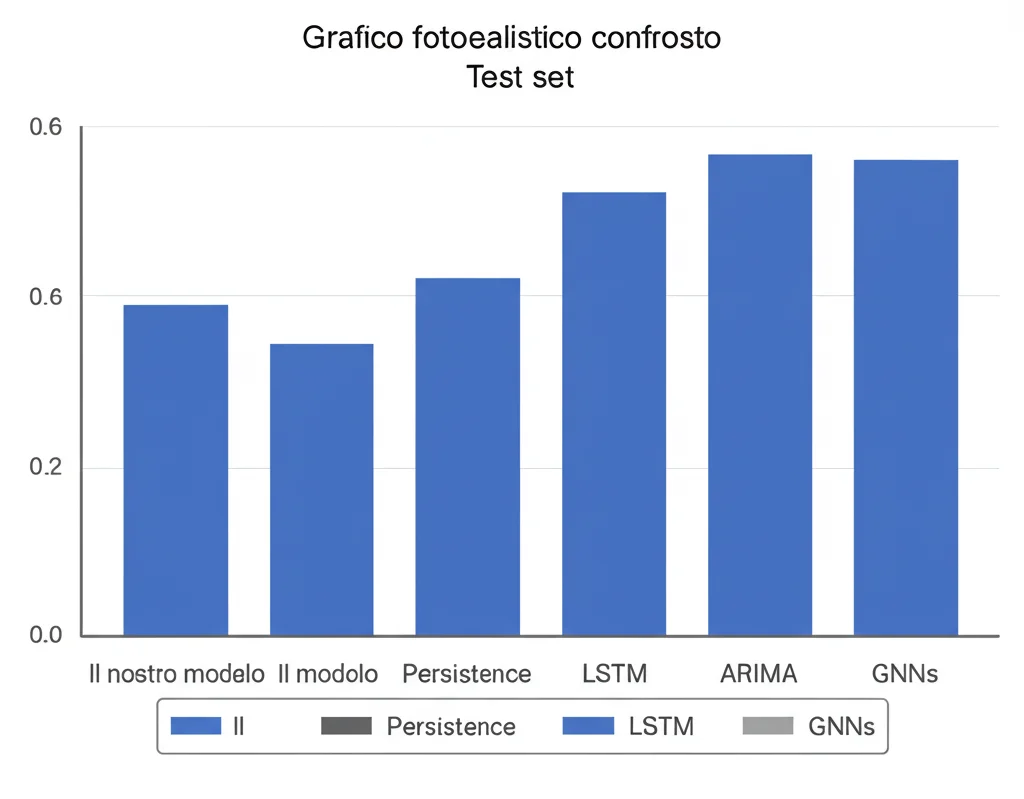
Abbiamo confrontato il nostro approccio con altri sei modelli:

• Persistence model: Prevede semplicemente che domani sarà come oggi. Sorprendentemente, data l’autocorrelazione dei dati, ha funzionato abbastanza bene, diventando un benchmark minimo da superare.
• LSTM: Una rete neurale ricorrente standard.
• LSTM con MLP: Un LSTM seguito da un MLP per la previsione.
• ARIMA: Un modello statistico classico per serie temporali.
• Due modelli GNN più complessi proposti in studi precedenti sullo stesso dataset.

Il nostro modello ha superato tutti gli altri nel test set! E la cosa più incredibile? Lo ha fatto con un numero di parametri drasticamente inferiore rispetto agli altri modelli di deep learning. Il nostro modello finale aveva solo 1.135 parametri, contro i 3.745 e 7.190 dei modelli GNN precedenti, o i 22.000-330.000 dei modelli basati su LSTM.

Questo risultato è fondamentale: dimostra che la nostra struttura, ispirata dalla matematica e quindi più semplice e mirata, è non solo efficace ma anche efficiente. Non serve una complessità esagerata per catturare le dinamiche essenziali della diffusione.

Il Valore Aggiunto: L’Interpretabilità

Ma l’accuratezza non è tutto. Ricordate il problema della “scatola nera”? Il nostro modello, essendo direttamente collegato alla struttura matematica, mantiene un buon grado di interpretabilità. Possiamo analizzare separatamente i contributi del ramo “generazione” e del ramo “diffusione”.

Ad esempio, abbiamo visualizzato questi due termini per la regione di Valencia. Il termine di generazione (arancione nel grafico del paper) ci dice quanto l’andamento interno passato della regione contribuisce ai nuovi casi. Il termine di diffusione (verde) ci dice quanto l’influenza delle regioni vicine, tramite i trasporti, sta pesando. Questo tipo di analisi può dare insight preziosi per capire *perché* i casi stanno aumentando o diminuendo in una certa area.

Certo, ci sono ancora sfide interpretative. A volte abbiamo visto valori di diffusione alti anche con pochi casi locali, o valori negativi difficili da spiegare biologicamente. Parte di questo potrebbe dipendere dai limiti dei dati (i dati sui trasporti erano pre-pandemia e non tenevano conto dei lockdown). Ma il potenziale c’è.

Guardando al Futuro

Cosa significa tutto questo? Abbiamo dimostrato che un approccio ibrido, che fonde la teoria matematica con la potenza del deep learning, può portare a modelli di previsione epidemica più accurati, efficienti e interpretabili.

Ci sono limiti, ovviamente. Il nostro modello attuale non sostituisce direttamente un SIR perché non modella esplicitamente suscettibili e guariti (a causa dei dati disponibili). E l’uso di dati di trasporto non aggiornati è una limitazione.

Ma la strada è aperta. Questo approccio potrebbe essere esteso usando dati più completi (come quelli che includono guariti e deceduti), permettendo stime dirette di parametri epidemiologici chiave. Potrebbe essere applicato ad altre malattie o regioni.

In sintesi, credo fermamente che combinare la conoscenza consolidata dei modelli matematici con le capacità di apprendimento flessibili delle reti neurali sia una direzione promettente. Offre uno strumento pratico ed efficace per supportare le strategie di sanità pubblica, permettendoci di reagire meglio e più velocemente alle future minacce epidemiche. È un piccolo passo, ma spero significativo, verso una migliore comprensione e gestione di queste sfide globali.

Fonte: Springer