Operatore di Sfocatura Tempo-Frequenza: Il Mio Segreto per Potenziare l’IA con Più Dati!

Amici appassionati di intelligenza artificiale e segnali, oggi voglio parlarvi di una chicca che mi ha davvero catturato: un operatore di sfocatura tempo-frequenza. Sembra un parolone, vero? Ma aspettate di sentire a cosa serve e come può darci una mano, specialmente quando si tratta di addestrare le nostre amate reti neurali con pochi dati a disposizione. Immaginate di poter “gonfiare” il vostro set di dati in modo intelligente, creando variazioni realistiche dei segnali originali. È un po’ come avere un trucco da prestigiatore per l’analisi dei segnali!

Cos’è questa Diavoleria della Sfocatura Tempo-Frequenza?

Partiamo dalle basi. Nell’analisi tempo-frequenza, noi non guardiamo un segnale (come un suono, o un segnale EEG) solo nel dominio del tempo o solo in quello delle frequenze, ma in entrambi contemporaneamente. È come avere una mappa dettagliata che ci dice quali frequenze sono presenti e in quale istante. Uno strumento chiave per fare questo è la Trasformata di Fourier a Breve Termine (STFT). Il risultato della STFT, o meglio, il suo modulo quadro, è quello che chiamiamo spettrogramma: una rappresentazione visiva, spesso colorata, dell’energia del segnale distribuita nel tempo e nelle frequenze. Pensatela come l’impronta digitale di un suono.

Ora, l’idea geniale che abbiamo esplorato è quella di “sfocare” o “spalmare” questa rappresentazione tempo-frequenza. In termini più tecnici, convolvere la STFT di un segnale con un “kernel” specifico, che è una sorta di piccolo filtro che definisce come avviene la sfocatura. Una volta fatta questa operazione, possiamo risintetizzare un nuovo segnale. Questo operatore l’abbiamo battezzato operatore di sfocatura tempo-frequenza o, più colloquialmente, STFT convolver.

Qualcuno potrebbe dire: “Ma non si faceva già qualcosa di simile?”. In effetti, lavori precedenti avevano esplorato concetti vicini, usando ad esempio convoluzioni “twisted” per rappresentare operatori più generali. La nostra svolta, però, è stata quella di usare una convoluzione standard, e questo cambia parecchio le carte in tavola per quanto riguarda le proprietà dell’operatore.

Perché Sbattersi Tanto? La Magia della Data Augmentation

La motivazione principale dietro questo studio è la data augmentation per il machine learning. Avete presente? Quando abbiamo pochi dati per addestrare un modello di intelligenza artificiale, una strategia è quella di creare artificialmente nuovi campioni partendo da quelli esistenti. Questo è cruciale in tantissimi campi: riconoscimento vocale, analisi di elettroencefalogrammi (EEG), classificazione di suoni e molto altro.

Con l’ascesa dei Vision Transformer (ViT), modelli potentissimi ma notoriamente “affamati” di dati (molto più delle classiche reti convoluzionali), la necessità di metodi di augmentation robusti è diventata ancora più pressante. Le tecniche standard includono l’aggiunta di rumore, la modifica del pitch o della velocità, la simulazione dell’eco di una stanza… cose così.

Recentemente, c’è stata molta attenzione sui metodi di augmentation che agiscono direttamente sullo spettrogramma, come il famoso SpecAugment, che maschera (cioè “cancella”) porzioni di tempo o di frequenza. Questi metodi sono facili da implementare, perché spesso le reti neurali usano proprio lo spettrogramma come input. C’è un però: gli spettrogrammi “aumentati” in questo modo potrebbero non corrispondere più a spettrogrammi di segnali reali, perché perdono certe proprietà di “liscezza”. Questo significa che i dati di addestramento potrebbero essere “fuori distribuzione” rispetto ai dati reali che il modello incontrerà. E se volessimo risintetizzare il segnale audio da uno spettrogramma modificato? Dovremmo usare algoritmi costosi e non sempre precisissimi, come l’algoritmo di Griffin-Lim, perché l’informazione di fase è andata persa.

Ecco dove il nostro operatore di sfocatura fa la differenza! Agendo sulla STFT prima di calcolare lo spettrogramma, manteniamo l’informazione di fase. Questo ci permette di risintetizzare un segnale audio in modo computazionalmente efficiente e, cosa importantissima, lo spettrogramma che otteniamo è “in-distribution”, cioè coerente con le proprietà dei segnali reali. Credo fermamente che i metodi di augmentation basati sullo spazio delle fasi (tempo-frequenza) siano uno strumento preziosissimo. Dopo i “moltiplicatori STFT” (come SpecAugment), l’introduzione di un “convolutore STFT” è un passo naturale e, a mio avviso, molto promettente.

Cosa Rende Speciale Questo Operatore?

L’idea è che il nostro operatore preservi le caratteristiche di alto livello dello spazio delle fasi, modificando solo la struttura locale. Cosa intendo? Che se un suono ha una nota fondamentale chiara con armoniche regolari, o un “chirp” (un suono la cui frequenza cambia rapidamente), queste macro-strutture vengono mantenute. Quello che cambia sono i pattern ad alta risoluzione nello spazio delle fasi. Questi pattern definiscono certamente parte del carattere del segnale, ma la struttura generale rimane intatta. È un po’ come sfocare leggermente una fotografia: i contorni principali restano, ma i dettagli fini si ammorbidiscono.

Abbiamo anche studiato a fondo le proprietà analitiche di questo operatore:

• Limitatezza: L’operatore non “esplode”, trasformando segnali con energia finita in segnali con energia infinita.
• Positività: Sotto certe condizioni sul kernel, l’operatore può essere positivo, una proprietà desiderabile in molti contesti.
• Non-compattezza: A differenza di altri operatori, questo, essendo basato su una convoluzione, non è compatto. Questo ha implicazioni teoriche su come “concentra” l’energia del segnale.

Questi aspetti, anche se possono sembrare astratti, ci danno intuizioni preziose su come scegliere il kernel e in quali contesti l’operatore può essere più utile.

Alternative e Generalizzazioni: Non Finisce Qui!

Una domanda sorge spontanea: perché non sfocare direttamente lo spettrogramma? L’abbiamo chiamato SpecBlur. È più semplice da implementare, e l’intuizione di “spalmare” il contenuto tempo-frequenza rimane. Tuttavia, come accennato, c’è il rischio che lo spettrogramma risultante non sia “realistico”. Nei nostri esperimenti, abbiamo visto che gli spettrogrammi sfocati con SpecBlur differiscono significativamente da quelli di segnali reali. Il nostro operatore STFT-blur, invece, produce risultati molto più simili a spettrogrammi autentici.

Si potrebbero anche immaginare generalizzazioni più complesse, come permettere al kernel di sfocatura di cambiare a seconda della posizione nel piano tempo-frequenza. Questo aprirebbe la strada a modelli ancora più flessibili, capaci magari di approssimare altri tipi di operatori o di effettuare una riduzione del rumore “intelligente”, come già esplorato in alcuni lavori con il nome di “Deep Filtering”. Per ora, ci siamo concentrati sulla versione più “semplice”, ma è un ottimo punto di partenza.

Mettiamolo alla Prova: Gli Esperimenti

Per vedere se tutta questa teoria reggeva alla prova dei fatti, abbiamo condotto degli esperimenti. Abbiamo preso il dataset SpeechCommands V2, che contiene registrazioni audio di 35 parole diverse, e abbiamo addestrato due tipi di modelli a classificarle:

• Una Rete Neurale Convoluzionale (CNN) basata sull’architettura ResNet-34.
• Un Vision Transformer (ViT) basato sull’architettura TinyViT-11M.

Questi due modelli rappresentano i paradigmi principali attuali per i sistemi di riconoscimento di immagini (e spettrogrammi, che sono immagini!).

L’aspetto cruciale era valutare l’effetto della data augmentation. Abbiamo limitato il numero di esempi di addestramento per ogni classe (100, 300, 600 o 1000 registrazioni) per simulare scenari “data-starved”, cioè con pochi dati. Come input per le reti, abbiamo usato i log-mel spettrogrammi (una versione dello spettrogramma scalata logaritmicamente e con frequenze raggruppate secondo la scala Mel, più percettiva per l’udito umano).

Abbiamo confrontato diverse configurazioni di augmentation:

• Nessuna augmentation (la nostra baseline).
• Solo aggiunta di rumore bianco.
• Solo SpecAugment (mascheramento tempo-frequenza).
• Solo il nostro STFT-blur.
• Solo SpecBlur.
• Combinazioni varie, inclusa una con tutte le augmentation.

Per ogni configurazione, abbiamo ripetuto l’addestramento più volte per ottenere medie di accuratezza affidabili.

I Risultati? Promettenti!

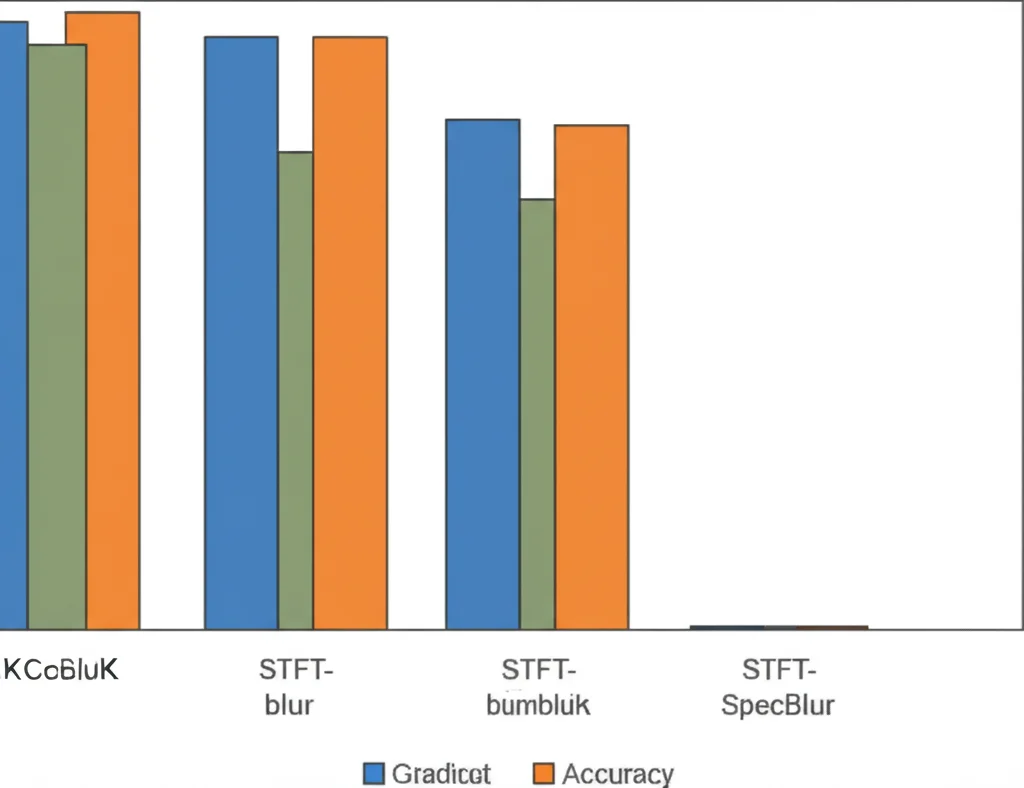
Ebbene, i risultati sono stati davvero incoraggianti! Sia con la CNN che con il ViT, l’introduzione del nostro STFT-blur e dello SpecBlur ha portato a miglioramenti significativi delle performance rispetto alla baseline, specialmente quando il numero di esempi di addestramento era basso. Questo è esattamente quello che speravamo: aiutare i modelli quando i dati scarseggiano!

In particolare, abbiamo notato che:

• Sia STFT-blur che SpecBlur hanno migliorato significativamente le prestazioni rispetto al non usare augmentation, per tutte le dimensioni del training set.
• Aggiungere una forma di “blurring” (STFT-blur o SpecBlur) sopra a tecniche classiche come l’aggiunta di rumore e SpecAugment ha portato a ulteriori miglioramenti significativi.
• Lo SpecBlur, pur essendo computazionalmente più efficiente, ha generalmente performato leggermente meglio di STFT-blur da solo, ma la combinazione di più metodi di augmentation ha spesso dato i risultati migliori in assoluto.

Per i Vision Transformer, che sono più sensibili alla quantità di dati, i guadagni di accuratezza dovuti all’augmentation sono stati ancora più evidenti rispetto alle CNN.

Conclusioni e Prospettive Future

Insomma, amici, questo operatore di sfocatura tempo-frequenza, insieme alla sua variante più semplice SpecBlur, si è dimostrato una tecnica di data augmentation promettente. Può migliorare le prestazioni sia delle reti convoluzionali che dei vision transformer quando lavorano con spettrogrammi, specialmente in scenari con pochi dati. Il fatto che STFT-blur operi mantenendo la coerenza della fase e producendo spettrogrammi “realistici” è un vantaggio teorico e pratico non da poco.

Certo, c’è ancora da esplorare: diversi tipi di kernel, l’applicazione a domini diversi dall’audio, e magari l’integrazione con le generalizzazioni più complesse che ho menzionato. Ma come primo passo, direi che ci siamo divertiti e abbiamo aperto una strada interessante. Chissà quali altre meraviglie ci riserva l’analisi tempo-frequenza applicata all’intelligenza artificiale!

Fonte: Springer