Onde Solitarie e Segreti Numerici: Svelando l’Approssimazione Iperbolica di KdV

Ciao a tutti! Oggi voglio portarvi con me in un viaggio affascinante nel mondo delle onde non lineari e delle equazioni che le descrivono. Avete mai sentito parlare dell’equazione di Korteweg-de Vries, o KdV? È una vera superstar nella fisica matematica, usata per descrivere onde solitarie (i famosi solitoni) in acque poco profonde, ma spunta fuori in tantissimi altri contesti. È elegante, integrabile, piena di proprietà meravigliose.

Recentemente, però, l’attenzione si è spostata anche su una sua “cugina” un po’ diversa: un’approssimazione iperbolica della KdV, che noi chiameremo affettuosamente KdVH. Questa nuova arrivata è stata proposta [4] con l’idea, tra le altre, di gestire meglio le condizioni al contorno nelle simulazioni numeriche. Ma, come spesso accade nella scienza, aprendo una porta se ne scoprono altre dieci!

Nel nostro lavoro, ci siamo tuffati a capofitto nello studio di questa KdVH. Volevamo capire che tipo di “bestia” fosse: che tipo di soluzioni ammette? Conserva qualcuna delle belle proprietà della KdV originale? E, soprattutto, come possiamo simularla al computer in modo efficiente e affidabile, preservandone la struttura matematica intrinseca?

Un Mondo Nascosto di Onde Viaggianti

La prima cosa che abbiamo scoperto è che la KdVH ha una vita propria decisamente ricca. Certo, possiede soluzioni a onda solitaria che assomigliano molto ai classici solitoni della KdV, e che tendono a coincidere con essi quando un certo parametro, chiamato parametro di rilassamento ((tau)), diventa molto piccolo. Questo è rassicurante: l’approssimazione fa il suo dovere!

Ma c’è di più. La KdV permette solitoni di altezza e velocità arbitrariamente grandi, il che non è sempre fisicamente realistico. La KdVH, invece, impone una sorta di “limite di velocità” a queste onde simili a solitoni. Già questo è interessante, perché sembra correggere un aspetto poco fisico del modello originale.

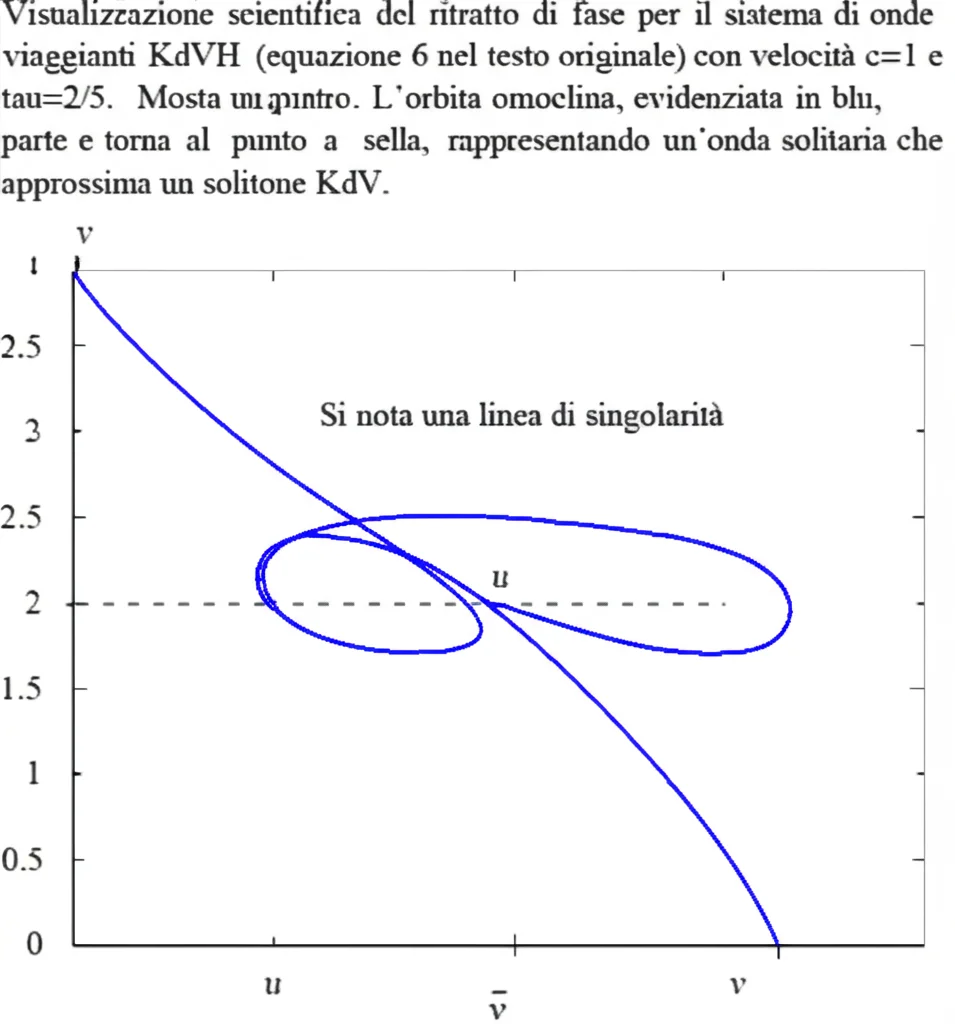
La vera sorpresa, però, è stata scoprire che la KdVH ospita anche altri tipi di onde viaggianti, sia solitarie che periodiche. Alcune di queste non hanno un corrispettivo diretto nella KdV, ma sembrano imparentate con soluzioni di altri modelli importanti per le onde marine, come le equazioni di Camassa-Holm e Degasperis-Procesi. Addirittura, alcune di queste nuove onde possono presentare delle singolarità, dei picchi molto accentuati! È come se la KdVH contenesse un universo di dinamiche più vasto di quello della KdV. Abbiamo analizzato queste nuove famiglie di onde, calcolandole numericamente con algoritmi specifici come quello di tipo Petviashvili. Vedere queste forme d’onda emergere dai calcoli è stato davvero elettrizzante!

Domare l’Equazione: Metodi Numerici che Rispettano la Struttura

Ok, abbiamo queste equazioni affascinanti, ma come le risolviamo numericamente? Qui entra in gioco la seconda parte del nostro lavoro: sviluppare metodi numerici “intelligenti”. Quando si ha a che fare con sistemi come la KdVH, che dipendono da un parametro ((tau)) che può diventare molto piccolo (il cosiddetto limite “stiff”), servono tecniche speciali.

Abbiamo puntato sui metodi Runge-Kutta Implicito-Espliciti (ImEx). L’idea è trattare implicitamente le parti dell’equazione che diventano “rigide” (difficili da gestire numericamente) quando (tau) è piccolo, e trattare esplicitamente le altre parti (tipicamente i termini non lineari). La scelta di *cosa* trattare implicitamente e *cosa* esplicitamente è cruciale! Abbiamo proposto uno splitting (una suddivisione dei termini) che si è rivelato molto efficace.

Il nostro obiettivo era duplice:

• Asymptotic Preserving (AP): Volevamo che i nostri metodi numerici, quando (tau) diventa piccolissimo, si comportassero automaticamente come un buon metodo numerico per l’equazione KdV originale. In pratica, lo schema numerico deve “capire” da solo qual è l’equazione limite e discretizzarla correttamente, senza che noi dobbiamo cambiare metodo al variare di (tau). Abbiamo dimostrato teoricamente questa proprietà per diverse classi di metodi ImEx (Tipo I e Tipo II), chiarendo anche condizioni aggiuntive come la “Globally Stiffly Accurate” (GSA) e l’importanza di dati iniziali “ben preparati” per alcuni metodi.
• Structure Preserving: La KdV ha delle quantità conservate (come massa ed energia). Anche la KdVH, pur non conservando esattamente l’energia della KdV, possiede una sua “energia modificata” che rimane costante nel tempo. È fondamentale che i metodi numerici rispettino queste leggi di conservazione, altrimenti le soluzioni simulate a lungo termine possono diventare completamente sbagliate!

Per ottenere la conservazione dell’energia a livello discreto, abbiamo usato due ingredienti chiave:

1. Operatori Summation-by-Parts (SBP) per la discretizzazione spaziale: Sono operatori differenziali discreti (basati su differenze finite, metodi Galerkin discontinui, o metodi spettrali) che mimano la proprietà fondamentale dell’integrazione per parti. Questo ci permette di replicare le dimostrazioni di conservazione dell’energia a livello discreto.
2. Tecnica di Rilassamento dell’Entropia (Entropy Relaxation): Anche se la discretizzazione spaziale è fatta bene, i metodi temporali standard (come i Runge-Kutta) non conservano esattamente l’energia. Questa tecnica modifica leggermente il passo finale del metodo Runge-Kutta, introducendo un parametro scalare (gamma_n) che viene aggiustato ad ogni passo temporale proprio per forzare la conservazione esatta dell’energia discreta. È un trucco elegante ed efficace!

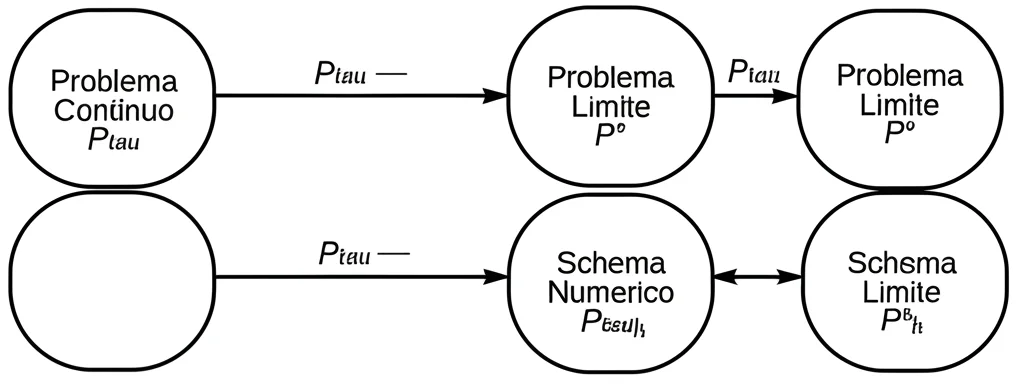P^0 (limite tau->0), P^tau -> P^tau_h (discretizzazione), P^0 -> P^0_h (discretizzazione), e la freccia cruciale P^tau_h -> P^0_h (limite tau->0, proprietà AP). Grafica informativa, stile pulito, frecce chiare. Fotografia concettuale, alta definizione.” />

La Prova dei Fatti: Esperimenti Numerici

Naturalmente, la teoria è bella, ma bisogna vedere se funziona in pratica! Abbiamo implementato i nostri metodi (usando Julia e librerie come SummationByPartsOperators.jl) e li abbiamo messi alla prova.

I risultati sono stati molto incoraggianti:

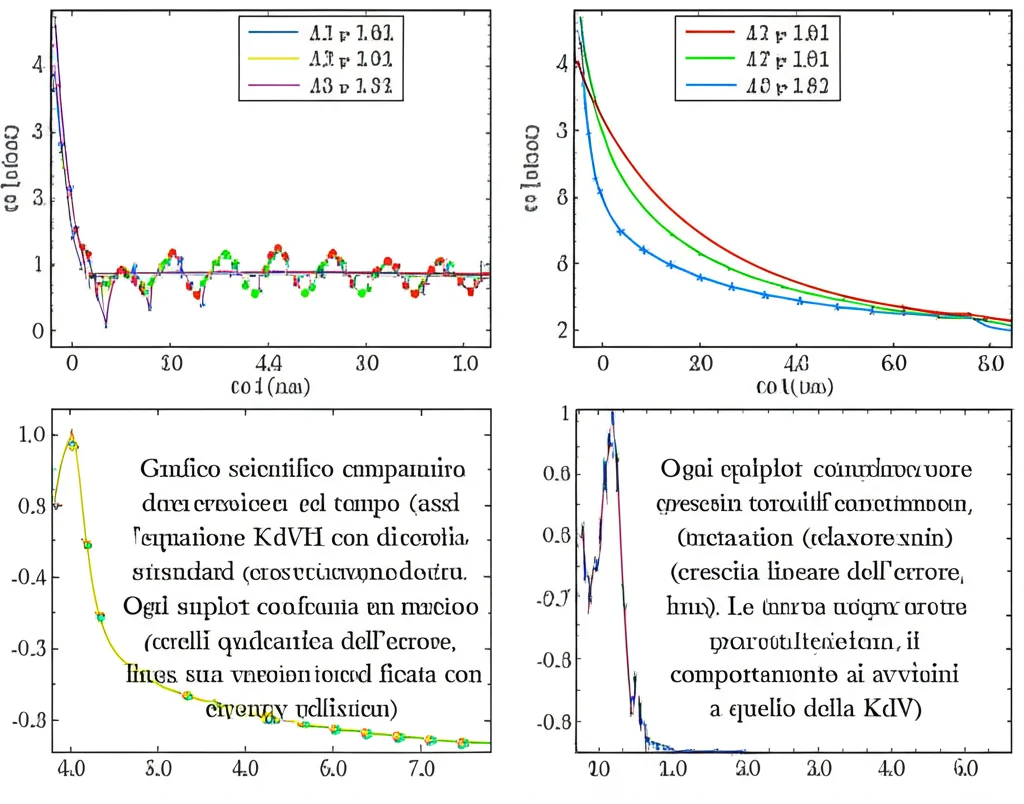
• Abbiamo verificato numericamente che le soluzioni della KdVH convergono a quelle della KdV quando (tau) diminuisce, proprio come previsto.
• Abbiamo confermato le proprietà AP e Asymptotically Accurate (AA) dei diversi schemi ImEx. È stato interessante notare che alcuni metodi si comportavano anche meglio di quanto la teoria garantisse strettamente, suggerendo che c’è ancora qualcosa da indagare a fondo.
• Abbiamo dimostrato l’importanza cruciale della conservazione dell’energia. Confrontando i metodi standard con quelli modificati tramite il rilassamento dell’entropia, abbiamo visto chiaramente quello che la teoria predice: i metodi conservativi mostrano una crescita dell’errore lineare nel tempo, mentre quelli non conservativi hanno una crescita quadratica. Questo significa che per simulazioni a lungo termine, usare un metodo conservativo è fondamentale per ottenere risultati accurati. Lo abbiamo testato sia con soluzioni a singolo solitone che con interazioni più complesse tra due solitoni.

Conclusioni e Prospettive Future

Che dire, esplorare la KdVH è stato un viaggio ricco di scoperte! Abbiamo visto che questa approssimazione iperbolica non è solo un “trucco” tecnico, ma un sistema con una dinamica propria, forse persino più ricca di quella della KdV originale, con connessioni inaspettate ad altri modelli di onde.

Dal punto di vista numerico, abbiamo sviluppato e analizzato metodi ImEx che sono robusti (grazie alla proprietà AP) e fedeli alla fisica del problema (grazie alla conservazione della struttura e dell’energia). Questi strumenti sono essenziali per poter studiare affidabilmente sistemi come la KdVH.

Certo, il lavoro non finisce qui. Sarebbe bellissimo investigare più a fondo le nuove famiglie di onde scoperte, capire meglio le loro proprietà e il loro significato fisico. E dal lato numerico, c’è sempre spazio per migliorare i metodi o esplorare la conservazione di altre quantità (la KdV ne ha infinite!).

Spero che questo racconto vi abbia incuriosito e vi abbia dato un’idea di come matematica, fisica e calcolo numerico si intreccino per svelare i segreti nascosti nelle equazioni che governano il nostro mondo. Alla prossima avventura scientifica!

Fonte: Springer