Prevedere il Sottosuolo: La Mia Svolta per Capire la Subsidenza (Anche Quando è Storta!)
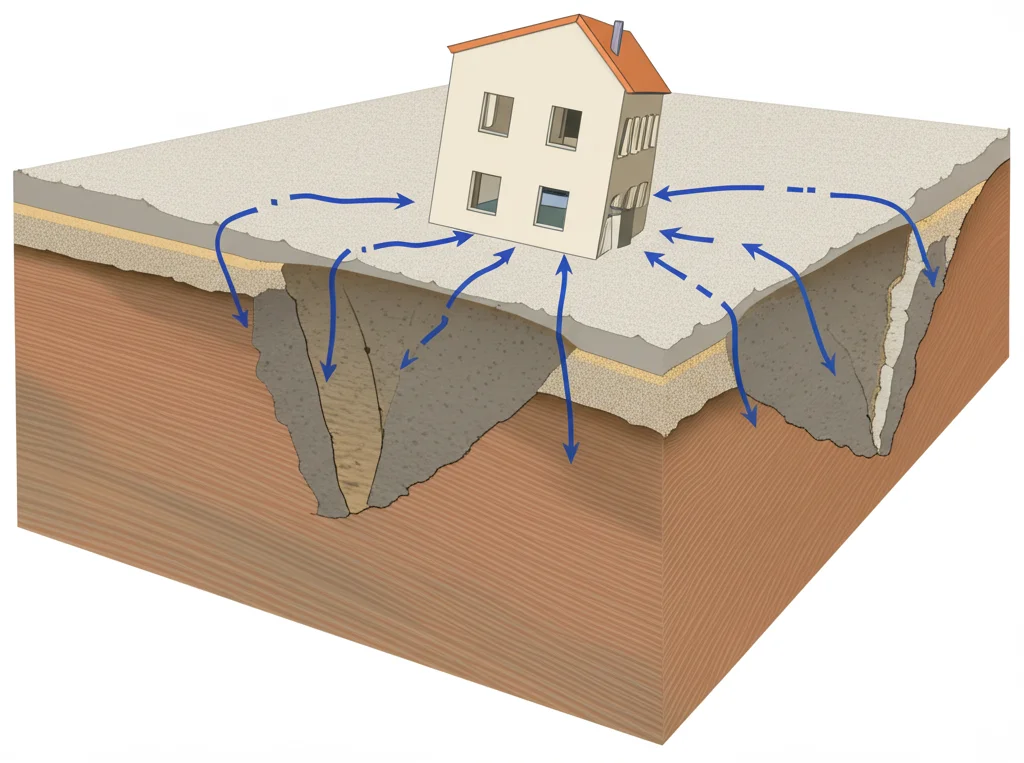
Ciao a tutti! Oggi voglio parlarvi di qualcosa che mi appassiona da tempo e che riguarda quello che succede proprio sotto i nostri piedi: la subsidenza. Immaginate il terreno che lentamente, quasi impercettibilmente, sprofonda. Questo fenomeno, spesso legato ad attività estrattive o allo svuotamento di cavità sotterranee come le caverne saline, non è solo affascinante dal punto di vista geologico, ma rappresenta un bel grattacapo per la sicurezza di edifici, infrastrutture e per l’ambiente.
Per anni, noi addetti ai lavori abbiamo usato modelli per prevedere come e quanto il terreno si abbasserà. Questi modelli sono fondamentali, perché capire dove e come il suolo si muoverà ci permette di gestire i rischi. Pensate ai danni che potrebbero verificarsi: crepe negli edifici, rottura di tubature, persino allagamenti in alcune aree. Ne abbiamo visti di esempi, purtroppo, in giro per il mondo.
Il Problema dei Vecchi Metodi: Troppo… Simmetrici!
I metodi classici, quelli che potremmo definire “standard”, funzionano alla grande in molte situazioni. Si basano sull’idea che lo sprofondamento crei una sorta di “conca” in superficie, la cui forma può essere descritta matematicamente, spesso usando una funzione che assomiglia alla famosa curva a campana di Gauss. Questi modelli, chiamati empirico-funzionali, sono relativamente semplici, usano pochi parametri e si basano sulla geometria del vuoto sotterraneo e sulla sua profondità. In Europa centrale, ad esempio, la distribuzione Gaussiana introdotta da pionieri come Litwiniszyn e Knothe negli anni ’50 è stata la regina indiscussa per decenni.
Il punto è che la realtà, come spesso accade, è più complicata e meno ordinata dei nostri modelli. Grazie a tecnologie di monitoraggio sempre più precise, come l’InSAR (Interferometria Radar Satellitare), e alla maggiore disponibilità di dati, abbiamo iniziato a notare che le “conche” di subsidenza reali sono spesso… beh, un po’ storte. Non sono perfettamente simmetriche e la loro forma non segue sempre alla lettera la curva a campana. A volte si osservano persino dei leggeri sollevamenti ai bordi della zona abbassata! Queste “anomalie” sono state osservate un po’ ovunque e sembrano legate, tra le altre cose, alle condizioni di stress presenti nelle rocce.
Tentativi Passati e i Loro Limiti
Ovviamente, non siamo stati con le mani in mano. Diversi ricercatori hanno proposto soluzioni per tener conto di queste stranezze. Per l’asimmetria, alcuni hanno introdotto angoli di influenza che variano con la direzione, o hanno “stirato” gli assi X e Y del modello. Per adattare la forma, si è pensato di modificare la matematica della funzione di influenza o di combinare due funzioni diverse.
Tutte idee valide, per carità. Ma ogni soluzione aveva i suoi difetti:
- Erano spesso complesse da usare.
- I nuovi parametri introdotti non sempre avevano un significato fisico chiaro.
- Una soluzione pensata per l’asimmetria non gestiva bene le deviazioni di forma, e viceversa. Mancava una visione d’insieme.
- Non erano sempre compatibili tra loro o con i metodi classici.
Insomma, avevamo tanti pezzi di un puzzle, ma mancava un modo per metterli insieme in maniera elegante ed efficace.

La Mia Proposta: Flessibilità è la Parola Chiave!
Ed è qui che entra in gioco il mio lavoro, la mia proposta. Ho pensato: perché non creare un metodo che gestisca sia l’asimmetria sia le deviazioni di forma, insieme o separatamente, e che rimanga comunque compatibile con l’approccio classico quando queste complicazioni non ci sono? L’obiettivo era chiaro: sviluppare uno strumento più flessibile e accurato per prevedere e gestire i rischi legati alla subsidenza.
L’idea di base è estendere le funzioni di influenza empiriche classiche, introducendo dei “controlli” specifici per la forma e l’asimmetria.
- Controllo della Forma: Abbiamo introdotto un “fattore di forma” (chiamato δ, delta) che permette di modificare la posizione del punto di massima inclinazione della conca di subsidenza. Avvicinandolo al centro, la conca diventa più profonda e stretta; allontanandolo, diventa più piatta e larga. Questo ci dà la flessibilità di adattarci a diverse “curvature” osservate nella realtà. La sfida qui è stata matematica: modificare questo aspetto rompeva la possibilità di calcolare facilmente il volume di subsidenza (che deve corrispondere al volume perso sottoterra, per la legge di conservazione!). Ho dovuto sviluppare una soluzione empirica, basata su simulazioni numeriche, per mantenere questo bilancio fondamentale.
- Controllo dell’Asimmetria: Abbiamo permesso al “raggio di influenza” (che definisce quanto lontano si estende l’effetto dello sprofondamento) di variare con la direzione (l’azimut). Immaginate una specie di ellisse invece di un cerchio perfetto. Questo permette di modellare le conche “sbilenche” che vediamo spesso. La direzione e l’entità di questa asimmetria possono essere definite basandosi sulle misure reali o su conoscenze geologiche (come la direzione degli stress principali nella roccia).
La cosa bella è che combinando questi due controlli, otteniamo un modello generale. Se impostiamo il fattore di forma a 2 (il valore classico) e il raggio di influenza costante, ritroviamo esattamente il modello Gaussiano tradizionale. Se modifichiamo solo uno dei due, otteniamo modelli che gestiscono solo la forma o solo l’asimmetria, simili ad alcune delle soluzioni proposte in passato, ma ora inserite in un quadro unificato.
Il Test sul Campo: Caverne Saline nel Nord della Germania
Le idee sono belle, ma funzionano? Per verificarlo, abbiamo applicato questo nuovo metodo a un caso di studio reale: un grande campo di caverne saline usate per lo stoccaggio di energia (gas, petrolio) nel nord della Germania (indicato come Europa Centrale nello studio originale). Parliamo di circa 89 caverne a 1500 metri di profondità, con volumi notevoli. Lì esiste una fitta rete di monitoraggio geodetico con circa 700 punti di livellazione, osservati regolarmente. Un sacco di dati preziosi!
Abbiamo usato questi dati per “calibrare” il nostro modello, cioè per trovare i valori migliori per i parametri (angolo di influenza, fattore di forma, direzione e intensità dell’asimmetria, ecc.). Abbiamo confrontato quattro scenari:
- Il metodo classico (simmetrico, forma Gaussiana).
- Il nostro metodo adattato solo per la forma (simmetrico, forma non Gaussiana).
- Il nostro metodo adattato solo per l’asimmetria (asimmetrico, forma Gaussiana).
- Il nostro metodo completo, unificato (asimmetrico, forma non Gaussiana).
I risultati della stima dei parametri sono stati già interessanti. È emersa chiaramente un’asimmetria, con lo sprofondamento massimo spostato rispetto all’asse verticale delle caverne, e una direzione preferenziale di questa asimmetria. Il fattore di forma ottimale era diverso da 2, confermando che la forma non era perfettamente Gaussiana. È stato affascinante vedere come i modelli che consideravano solo un aspetto (forma o asimmetria) cercassero di “compensare” l’altro mancante, mentre il modello unificato riusciva a trovare un equilibrio migliore tra tutti i parametri.
I Risultati: Un Bel Salto di Qualità!
Ma veniamo al dunque: quanto è migliorata la previsione? Abbiamo usato diversi indicatori statistici per confrontare le previsioni dei modelli con le misure reali. L’errore quadratico medio (MSE), l’errore assoluto medio (MAE), la deviazione standard (STD) dei residui (le differenze tra previsione e realtà), il coefficiente di determinazione (R2)… tutti parametri che ci dicono quanto il modello “ci azzecca”. Abbiamo anche considerato criteri come AIC e BIC, che valutano il compromesso tra accuratezza e complessità del modello (più parametri = più complesso).
I numeri parlano chiaro: il nostro nuovo approccio unificato ha superato tutti gli altri. Rispetto al metodo classico, abbiamo ottenuto una riduzione dell’errore quadratico medio fino al 25%! E anche rispetto ai metodi che affrontavano solo la forma o solo l’asimmetria, il miglioramento è stato significativo (fino al 12%).
Analizzando i residui, abbiamo visto che il metodo classico tendeva a sottostimare la subsidenza massima e a sovrastimarla in altre zone, con una distribuzione degli errori un po’ sbilanciata. Il nostro metodo unificato, invece, ha prodotto errori più piccoli in media, distribuiti in modo più simmetrico attorno allo zero e più vicini a una distribuzione normale. Questo significa che il modello cattura meglio i pattern reali del fenomeno.
Anche le mappe dei residui sono state illuminanti. La mappa del metodo classico mostrava chiaramente le zone dove il modello sbagliava di più, evidenziando i problemi legati sia alla forma che all’asimmetria. Le mappe dei modelli intermedi miglioravano l’una o l’altra cosa, ma solo la mappa del modello unificato mostrava una riduzione complessiva degli errori su tutta l’area, coprendo sia l’asimmetria che adattando meglio la forma della conca.

Cosa Significa Tutto Questo?
Questa ricerca, secondo me, dimostra una cosa importante: per prevedere bene la subsidenza, soprattutto in contesti geologicamente complessi come le cupole saline dove gli stress orizzontali possono essere elevati, dobbiamo considerare che la forma dello sprofondamento può deviare dalla classica campana Gaussiana e che il processo è spesso asimmetrico.
Il nuovo metodo che abbiamo sviluppato fa proprio questo: integra flessibilità di forma e asimmetria in un unico modello coerente. Non è una rivoluzione che butta via il passato, ma un’evoluzione che estende i metodi classici per coprire casi più complessi, quelli che prima ci davano filo da torcere.
Questo approccio unificato ci fornisce uno strumento più potente e affidabile per l’analisi dei rischi e la gestione delle aree interessate da subsidenza. E chissà, forse ci aiuta anche a capire meglio perché la subsidenza si comporta così, suggerendo che gli stress esterni giocano un ruolo chiave nel “modellare” la forma dello sprofondamento più di quanto pensassimo. Ma questa è un’altra storia, per un’altra volta!
Fonte: Springer