Prevedere il Clima con l’IA: Un Nuovo Modello di Temperatura per Rivoluzionare i Derivati Meteorologici

Ciao a tutti! Oggi voglio parlarvi di un argomento che mi sta particolarmente a cuore e che, credetemi, sta per cambiare le carte in tavola nel mondo della finanza e della gestione dei rischi climatici. Sto parlando di come possiamo usare l’intelligenza artificiale, e in particolare le reti neurali, per modellare la temperatura in un modo completamente nuovo e, oserei dire, affascinante. Immaginate di poter prevedere con precisione millimetrica come varierà la temperatura non solo in un punto specifico, ma su intere aree geografiche, anche dove non ci sono stazioni meteo! Sembra fantascienza? Beh, continuate a leggere e vi mostrerò che è più reale di quanto pensiate.

Il Clima Bussa alla Porta (del Portafoglio)

Partiamo da un fatto: il meteo, con i suoi capricci, ha un impatto enorme su un sacco di attività economiche. Pensateci un attimo: produttori di energia, catene di supermercati, l’industria del turismo, il settore agricolo… tutti, in un modo o nell’altro, sentono il peso delle bizze del tempo. Questa vulnerabilità rende fondamentale trovare modi per proteggersi, per “coprirsi” da questi rischi. E qui entrano in gioco i derivati meteorologici.

Cosa sono? In parole povere, sono strumenti finanziari il cui valore dipende da variabili meteorologiche come la temperatura, le precipitazioni, l’umidità o la neve. La stragrande maggioranza di questi, circa il 98-99%, è legata a un indice di temperatura. Contratti che usano metriche come i Gradi Giorno di Riscaldamento (HDD – Heating Degree Days) e i Gradi Giorno di Raffreddamento (CDD – Cooling Degree Days) sono all’ordine del giorno. Questi misurano quanto la temperatura si discosta da un valore base. Avere un buon modello per l’evoluzione della temperatura è, quindi, la spina dorsale per prezzare correttamente questi derivati. Un modello accurato garantisce che i derivati offrano una protezione efficace e aiuta le istituzioni finanziarie a gestire i loro portafogli, capendo correlazioni e varianze nei pattern di temperatura. E non solo: prezzare correttamente significa evitare che siano troppo cari o troppo economici, portando a un mercato più equo. Con i cambiamenti climatici che rimescolano le carte, avere modelli dinamici e precisi è ancora più cruciale.

Però, creare un modello accurato per la temperatura giornaliera è un bel rompicapo. Le temperature osservate mostrano stagionalità nella media, nella varianza, nella distribuzione e nelle autocorrelazioni, per non parlare della “memoria lunga” in queste ultime. Un approccio comune è usare processi continui di Ornstein-Uhlenbeck. Una volta stimato il processo, si può valutare qualsiasi strumento derivato calcolando il valore atteso del payoff futuro scontato. Ma anche qui, i problemi non mancano. Primo, se l’attività sottostante è l’indice di temperatura o i gradi giorno, le opzioni call e put su HDD sono opzioni di tipo “asiatico” (il cui payoff dipende dalla media del sottostante su un periodo). Secondo, il mercato meteorologico è incompleto: il sottostante (la temperatura) non si può immagazzinare o scambiare. Questo rende inefficaci i meccanismi di pricing basati sull’assenza di arbitraggio, perché i derivati meteorologici non possono essere replicati con altri strumenti finanziari. In questi casi, spesso si ricorre alle simulazioni Monte Carlo.

Vecchi Modelli e Nuove Sfide: il Rischio di Base Geografico

Nel campo della valutazione dei derivati meteorologici, sono stati proposti vari modelli. Alaton et al. (2002) proposero un processo mean-reverting (che tende a tornare verso una media) con varianza costante per ogni mese. Brody et al. (2002) introdussero un modello frazionario, più realistico ma complesso. Benth e Šaltytė-Benth (2005, 2007) svilupparono un framework stocastico che considera la natura mean-reverting e la stagionalità. Altri hanno aggiunto complessità come la velocità di mean-reversion dipendente dal tempo o indici di temperatura basati su medie ponderate di diverse località. Tra tutti, il modello di Alaton et al. (2002) spicca per il suo equilibrio tra complessità e praticità.

Uno dei nodi cruciali quando si parla di derivati meteorologici è scegliere l’area geografica giusta per cui il contratto è scritto. Un derivato potrebbe essere poco efficace nel coprire il rischio climatico in un’area lontana dalla stazione di riferimento del contratto o con microclimi particolari (coste, montagne). Questo problema è noto come rischio di base geografico o spaziale. Non solo interferisce con la corretta valutazione del derivato e la sua efficacia, ma genera anche sfiducia nello strumento. Pensate all’Italia: un paese che si estende per circa dieci gradi di latitudine, con montagne, coste, pianure… un vero mosaico climatico! Usare dati che approssimano il rischio basandosi sulle caratteristiche climatiche specifiche di un’area mitiga questo rischio di base geografico.

Negli ultimi anni, l’uso di dati satellitari ha migliorato l’affidabilità delle assicurazioni basate su indici per coprire eventi climatici avversi, e risultati incoraggianti si possono ottenere anche nel pricing dei derivati meteorologici. Per l’Italia, studi hanno mostrato come gli effetti del rischio climatico, ad esempio sull’agricoltura, siano molto disomogenei geograficamente.

La Nostra Proposta: Un Modello di Temperatura Spazialmente Continuo con Reti Neurali (SCNNT)

Ed eccoci al cuore della nostra innovazione. Abbiamo sviluppato un modello di temperatura spazialmente continuo. Cosa significa? Che la temperatura è rappresentata come una funzione delle coordinate di longitudine e latitudine, definite come numeri reali. Questo ci permette di descrivere la dinamica della temperatura in qualsiasi punto all’interno della zona di interesse, anche se non ci sono dati di temperatura disponibili per quella specifica località! È un po’ come avere una mappa termica ad altissima risoluzione che si aggiorna dinamicamente.

Per “imparare” questa funzione complessa, usiamo dati satellitari e, qui sta il bello, le reti neurali profonde (Deep Neural Networks – DNNs). Le DNNs sono modelli computazionali sofisticati, composti da neuroni interconnessi disposti in più strati, capaci di catturare relazioni complesse nei dati. Nonostante questa complessità, abbiamo progettato l’architettura della rete neurale in modo da mantenere la spiegabilità del modello. Come? Mantenendo la struttura del modello di Alaton et al. (2002) a livello dello strato di output della rete. In pratica, usiamo le reti neurali per “scoprire” i parametri ottimali di un modello già noto e interpretabile, ma lo facciamo in modo continuo su tutto lo spazio geografico.

Formalmente, i parametri del modello di Alaton (come la temperatura media A, l’effetto marginale giornaliero B, l’ampiezza della stagionalità C, la fase della stagionalità φ, il coefficiente di mean-reversion α e la volatilità σ) diventano funzioni continue delle coordinate (u,v): A(u,v), B(u,v), ecc. Per la volatilità σ(u,v,m), abbiamo anche una dipendenza dal mese ‘m’, che è una variabile categorica. Per gestire quest’ultima, usiamo uno strato di “Embedding” nella rete neurale, che impara una rappresentazione numerica per ogni mese. Per le coordinate geografiche, usiamo strati “Fully-Connected” (FCN). La cosa fantastica è che calibriamo il modello una sola volta per tutti i punti della zona di interesse, sfruttando così le dipendenze spaziali nelle dinamiche di temperatura e usando i dati in modo più efficiente.

Mettiamo alla Prova il Modello: L’Italia Sotto la Lente

Per testare il nostro modello SCNNT (Spatially-Continuous Neural Network Temperature model), abbiamo usato i dati satellitari NASA-MERRA-2, che forniscono dati atmosferici su una griglia di circa 50 km per lato. Abbiamo selezionato un’area rettangolare che copre l’Italia, per un totale di 500 pixel (20 livelli di longitudine e 25 di latitudine), usando dati di temperatura media giornaliera dal 2010 al 2023. L’Italia, con la sua estensione latitudinale e le sue differenze morfologiche (Alpi, Appennini, coste, pianure), è un banco di prova perfetto.

I risultati sono stati sorprendenti! Confrontando le stime dei parametri ottenute con l’approccio pixel per pixel di Alaton et al. e quelle del nostro SCNNT, abbiamo visto che il nostro modello cattura le caratteristiche morfologiche dell’Italia con un livello di dettaglio superiore. Ad esempio, per il parametro A (temperatura media), l’SCNNT delinea i confini tra aree montane e valli con maggiore granularità. Anche per gli altri parametri (B, C, φ, α, σ), le mappe generate dall’SCNNT mostrano pattern coerenti con la morfologia del territorio e spesso più dettagliati. Ad esempio, il parametro C (ampiezza della stagionalità) mostra chiaramente l’azione termoregolatrice del Mar Mediterraneo, con escursioni termiche minori sul mare e sulle coste.

Per una validazione “out-of-sample” spaziale, abbiamo preso i dati di una stazione meteo reale (Fiumicino Maccarese) non posizionata al centro di un pixel della griglia MERRA-2. Confrontando le temperature osservate con quelle previste dal nostro SCNNT per le coordinate esatte della stazione, abbiamo visto che il modello cattura accuratamente le dinamiche di temperatura, dimostrando la sua efficacia anche per punti non usati direttamente nella calibrazione.

Implicazioni Pratiche: Prezzare i Derivati HDD con Maggiore Precisione

Ma a cosa serve tutto questo in pratica? Beh, per esempio, a prezzare i derivati meteorologici in modo più accurato. Abbiamo considerato un’opzione call su HDD. Immaginate che un contratto del genere sia disponibile per Roma e un’azienda di Milano voglia usarlo per coprirsi dal rischio legato alle temperature milanesi. Sarà costretta a comprare un derivato basato sulla temperatura di Roma. Noi vogliamo mostrare che un modello che fornisce informazioni sulla temperatura in qualsiasi punto può definire uno strumento di copertura più appropriato.

Abbiamo simulato il payoff di un’opzione call HDD con scadenza 31/03/2023, emessa il 01/01/2023, con strike K=600 giorni-grado, usando le previsioni di temperatura del nostro SCNNT per Roma, Maccarese (vicino Roma) e Milano. I risultati? Notevoli! Il payoff atteso per Roma era 238.83. Per Maccarese, nonostante la vicinanza, 109.18. Per Milano, ben 616.25! Questo evidenzia l’enorme variabilità spaziale del rischio legato alla temperatura e l’importanza delle condizioni locali nel prezzare questi strumenti. Un’azienda milanese che si coprisse con un derivato su Roma potrebbe trovarsi o sotto-coperta o sovra-coperta.

Non Finiamo Qui: Estensioni e Sviluppi Futuri

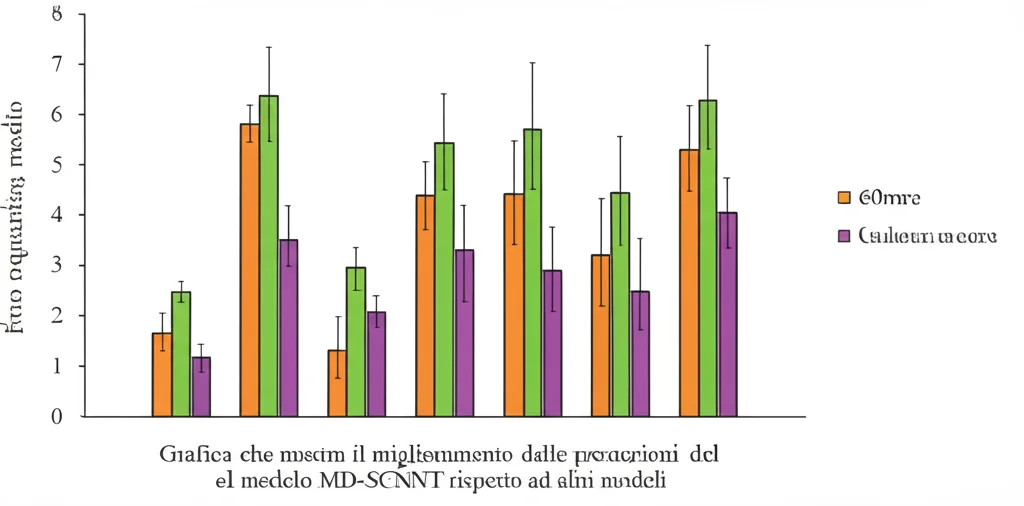
Il bello del nostro modello SCNNT è la sua flessibilità. Possiamo estenderlo in vari modi. Ad esempio, abbiamo provato a rendere il parametro C (ampiezza della stagionalità) dipendente anche dal mese (MD-SCNNT). Questo ha aumentato ulteriormente la flessibilità e, nei nostri esperimenti, ha migliorato le performance di previsione dal 3.3% al 5.2% rispetto al modello di Alaton.

Cosa ci riserva il futuro? Beh, abbiamo diverse idee. Innanzitutto, vogliamo incorporare l’altitudine nel modello, un fattore cruciale. Poi, puntiamo a introdurre un modello dinamico per la volatilità della temperatura. E infine, esploreremo architetture di reti neurali specifiche per dati sequenziali, come le reti LSTM (Long Short-Term Memory), perfette per sfruttare la struttura di serie storica dei dati di temperatura.

In conclusione, credo fermamente che questo approccio basato su reti neurali per modellare la temperatura in modo spazialmente continuo apra scenari incredibilmente promettenti. Non solo ci permette di valutare il rischio climatico con una precisione mai vista prima, ma migliora anche la valutazione dei derivati meteorologici, rendendoli strumenti più efficaci e affidabili. È un passo avanti significativo, e sono entusiasta di vedere dove ci porterà questa strada!

Fonte: Springer