Prevedere il Terreno che Cede: Il Mio Nuovo Modello Adattivo Basato sui Dati Reali

Avete mai pensato a cosa succede sotto i nostri piedi quando si scava una miniera? Il terreno può cedere, un fenomeno chiamato subsidenza, e questo può creare non pochi problemi all’ambiente e alle strutture che si trovano in superficie, come strade, edifici o linee elettriche. Capire quando e quanto il terreno si abbasserà è fondamentale per poter intervenire in tempo con manutenzioni o rinforzi. Il problema è che prevederlo con precisione è sempre stata una bella sfida.

I metodi tradizionali, diciamocelo, hanno i loro limiti. Spesso si basano su modelli matematici con parametri fissi che faticano ad adattarsi ai cambiamenti reali che avvengono durante l’estrazione mineraria. La velocità di scavo può variare, la geologia del sottosuolo è complessa… insomma, usare un modello “taglia unica” porta spesso a previsioni poco accurate. E una previsione sbagliata può significare scegliere la strategia di intervento errata, intervenire troppo presto o troppo tardi, o calcolare male i volumi necessari per le riparazioni.

Proprio per superare questi limiti, ho lavorato allo sviluppo di qualcosa di nuovo: un modello predittivo adattivo per la subsidenza dinamica, che ha un asso nella manica: si aiuta con i dati misurati direttamente sul campo. L’idea è semplice ma potente: invece di affidarci a parametri teorici fissi, usiamo le misurazioni storiche della subsidenza per “insegnare” al modello come si sta comportando realmente il terreno in quella specifica situazione.

Il Vecchio Metodo e i Suoi Limiti

Facciamo un passo indietro. Uno dei metodi più usati in Cina, e incorporato anche nelle normative di settore, è il Modello a Integrale di Probabilità (PIM). Questo modello, basato sulla teoria dei mezzi casuali, immagina il movimento del terreno come quello di un mezzo granulare. Si divide l’area di scavo in tante piccole unità e si calcola l’effetto cumulativo di ciascuna unità sulla superficie.

Per prevedere la subsidenza nel tempo (la cosiddetta subsidenza dinamica), il PIM viene spesso combinato con delle “funzioni temporali”. Una delle più classiche è la funzione di Knothe. Questa funzione ha una solida base matematica, ma ha un punto debole: si basa su un parametro, chiamato ‘c’, che dovrebbe rappresentare l’effetto di ritardo con cui la subsidenza si propaga attraverso gli strati rocciosi sovrastanti la miniera.

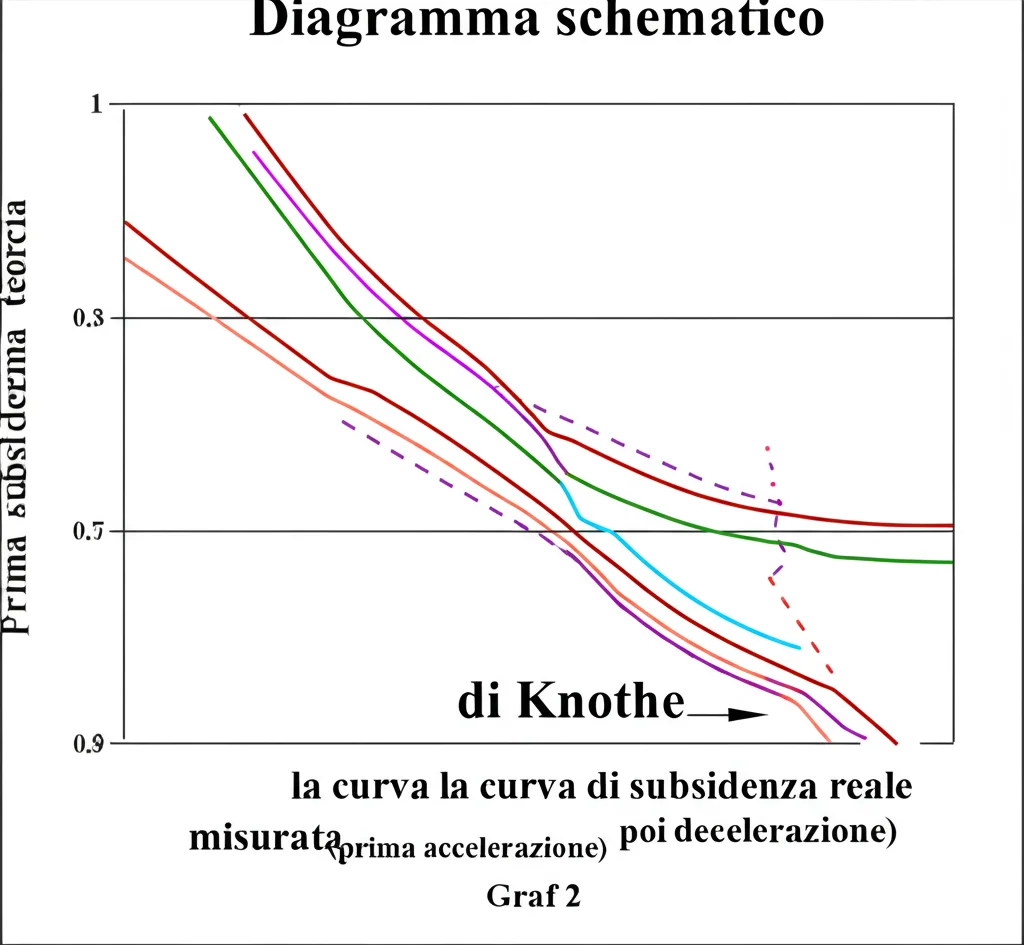
Il problema è che questo parametro ‘c’, nei modelli classici, viene spesso calcolato con formule che lo considerano più o meno costante, magari legato solo alla velocità media di avanzamento dello scavo e alla profondità. Ma la realtà è molto più dinamica! Pensateci: all’inizio dello scavo, le rocce sopra la miniera sono ancora integre e resistono bene. L’effetto ritardo è massimo, quindi ‘c’ dovrebbe avere un certo valore (anzi, all’inizio proprio zero, poi un picco). Man mano che lo scavo procede, la struttura rocciosa inizia a cedere, la sua capacità di carico diminuisce, l’energia accumulata si rilascia e la subsidenza accelera. L’effetto ritardo cala drasticamente, e così dovrebbe fare il valore di ‘c’. Poi, con l’avanzare dello scavo, la roccia subisce deformazioni e rotture periodiche, facendo oscillare questo effetto ritardo e, di conseguenza, il valore di ‘c’.

Insomma, il parametro ‘c’ non è affatto costante! È un valore che cambia continuamente. Usare un valore fisso o calcolato con formule semplicistiche è uno dei motivi principali per cui le previsioni dinamiche tradizionali spesso non ci azzeccano. Il modello di Knothe, con un ‘c’ fisso, descrive un processo di subsidenza con accelerazione decrescente, mentre nella realtà i punti in superficie prima accelerano e poi decelerano la loro discesa. Una bella differenza!

La Nostra Idea Geniale: Un Modello che Impara

Ecco dove entra in gioco la mia proposta: un modello predittivo dinamico adattivo supportato da dati misurati. L’idea chiave è sfruttare le misurazioni che, specialmente in presenza di strutture importanti in superficie (come autostrade, ferrovie ad alta velocità, tralicci dell’alta tensione), vengono comunque fatte frequentemente durante il periodo di estrazione mineraria per motivi di sicurezza.

Come funziona? Immaginiamo di dover prevedere la subsidenza quando lo scavo arriverà alla posizione (d_{N+1}). Se abbiamo già raccolto dati di misurazione per N periodi precedenti, il processo è questo:

• Passo 1: Guardare indietro. Prendiamo i dati misurati degli ultimi M periodi (ad esempio, gli ultimi 4 o 5 periodi). Per ciascuno di questi periodi passati, “invertiamo” il modello per trovare quale sarebbe stato il valore ottimale del parametro ‘c’ che avrebbe prodotto esattamente la subsidenza misurata. Otteniamo così una sequenza degli ultimi valori ottimali di ‘c’: ((c_{N}), (c_{N-1}), …, (c_{N-M+1})).
• Passo 2: Individuare il trend. Analizziamo questa sequenza di valori ottimali di ‘c’ insieme alle corrispondenti posizioni di avanzamento dello scavo ((d_{N}), (d_{N-1}), …, (d_{N-M+1})). Usiamo un modello di estrapolazione per prevedere quale sarà il valore più probabile di ‘c’ (chiamiamolo (c_{N+1})) quando lo scavo raggiungerà la posizione successiva (d_{N+1}).
• Passo 3: Prevedere il futuro. Usiamo questo valore estrapolato (c_{N+1}), insieme alle informazioni sullo scavo alla posizione (d_{N+1}), per calcolare la previsione della subsidenza dinamica (S_{N+1}) con il nostro modello PIM/Knothe “aggiornato”.
• Passo 4: Ripetere. Man mano che lo scavo avanza e raccogliamo nuovi dati di misurazione, ripetiamo i passi 1-3 per prevedere la subsidenza per le posizioni successive.

Per l’estrapolazione del parametro ‘c’ (Passo 2), ho scelto di usare un approccio chiamato Modello di Previsione Grigio (Gray Prediction Model) con una logica “Metabolism”. Questo modello è ottimo perché richiede pochi dati storici (il che è utile, perché spesso le campagne di monitoraggio non producono quantità enormi di dati), ha una buona accuratezza e non necessita di informazioni a priori complesse. La parte “Metabolism” significa che diamo più peso ai dati più recenti, scartando quelli più vecchi, per catturare meglio le tendenze attuali. Di solito bastano i dati degli ultimi 4 periodi ((M=4)) per fare una buona estrapolazione.

Ovviamente, gestire tutti questi dati e parametri richiede un certo lavoro computazionale. Per questo, ho sviluppato il modello implementandolo in un programma per computer (usando Visual Basic), dividendolo in moduli per gestire l’acquisizione dati, la previsione PIM e la gestione dei parametri geologici e minerari. Questo rende il tutto più efficiente. Su un normale PC, fare previsioni per migliaia di punti richiede solo pochi secondi, il che è perfettamente adeguato per le esigenze ingegneristiche.

La Prova sul Campo: Il Caso della Miniera di Nantun

Per vedere se questo approccio funzionava davvero, l’abbiamo messo alla prova in un caso reale: la miniera di carbone di Nantun, nella provincia di Shandong in Cina. Qui, il fronte di scavo 7321 (ovest) passava proprio sotto un’autostrada ad alta percorrenza. Come potete immaginare, l’autostrada ha iniziato a subire danni significativi, come crepe e avvallamenti, man mano che lo scavo procedeva sotto di essa.

Durante il periodo di scavo (da febbraio ad agosto 2013), sono state installate delle stazioni di monitoraggio direttamente sul manto stradale per misurare con precisione la subsidenza verticale. Sono state effettuate 19 campagne di misurazione, raccogliendo una grande quantità di dati preziosi.

Abbiamo quindi usato questi dati per confrontare le previsioni del modello classico (con il parametro ‘c’ calcolato secondo la formula tradizionale) e quelle del nostro nuovo modello adattivo (che estrapolava ‘c’ usando i dati misurati dei 4 periodi precedenti).

I risultati? Davvero incoraggianti! Il valore ottimale di ‘c’ variava significativamente da periodo a periodo, confermando che un valore fisso non era adeguato. Il modello classico, usando la formula tradizionale, aveva un errore relativo medio nel calcolo di ‘c’ del 40.1%. Il nostro modello adattivo, invece, riusciva a prevedere ‘c’ con un errore quasi sempre inferiore al 10%.

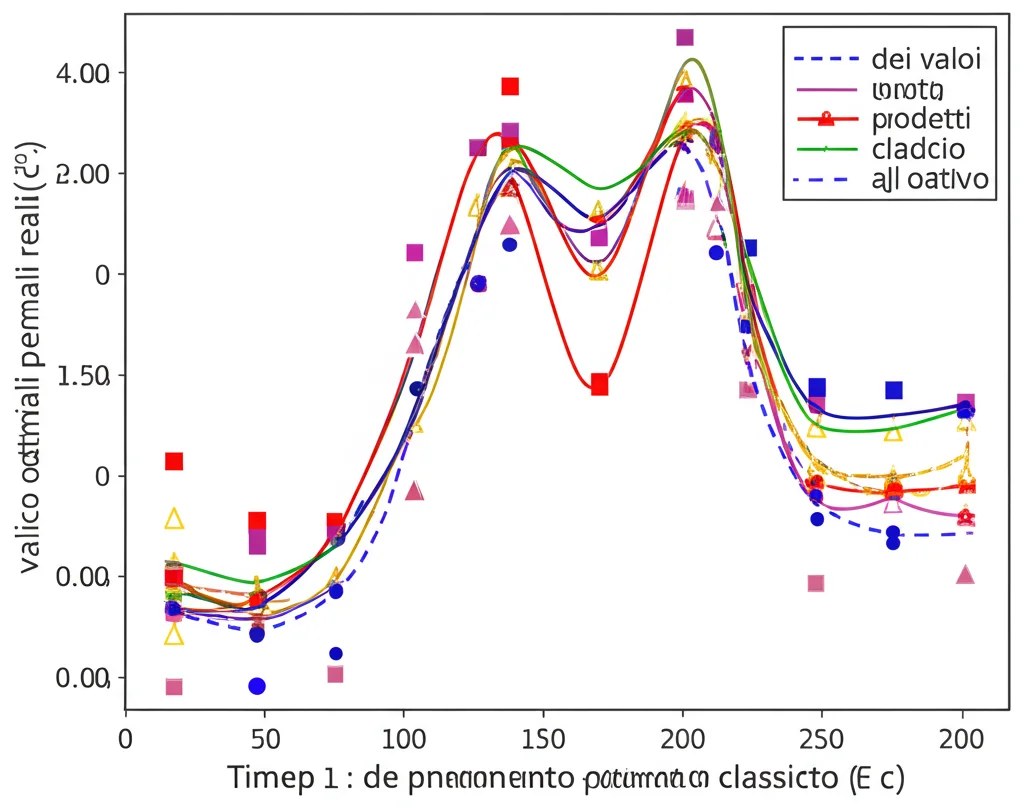
Ma la cosa più importante è l’accuratezza della previsione della subsidenza finale. Abbiamo usato l’Errore Quadratico Medio Relativo (RMSE relativo) come metrica.

• Il modello classico ha mostrato un RMSE relativo medio del 9.1%, con picchi fino al 15.3%.
• Il nostro modello adattivo ha ottenuto un RMSE relativo medio del 4.3%, con un massimo del 6.0%.

Un miglioramento netto! L’errore medio è stato praticamente dimezzato. Analizzando i singoli punti di monitoraggio sull’autostrada, sia quelli al centro dell’area di scavo che quelli ai bordi, il modello adattivo ha mostrato errori massimi molto più contenuti (intorno al 4.7-6.9% rispetto alla subsidenza finale) rispetto al modello classico (16.5-24%).

Perché è Importante Questo Passo Avanti?

Questo miglioramento nell’accuratezza non è solo un esercizio accademico. Ha implicazioni pratiche enormi. Previsioni più precise significano:

• Pianificare meglio gli interventi di manutenzione e rinforzo delle strutture in superficie.
• Intervenire al momento giusto, né troppo presto (sprecando risorse) né troppo tardi (rischiando danni maggiori).
• Stimare più accuratamente i volumi di materiali necessari (ad esempio, per iniezioni di consolidamento nel sottosuolo).
• Garantire una maggiore sicurezza per le infrastrutture critiche e per chi le utilizza.

Il modello adattivo, sfruttando i dati di monitoraggio che spesso sono già disponibili, fornisce un supporto tecnico robusto per gestire gli effetti della subsidenza in modo più efficace ed efficiente.

Uno Sguardo al Futuro

Certo, c’è sempre spazio per migliorare. Con l’avanzare delle tecnologie di monitoraggio (sensori, telerilevamento) e di trasmissione dati, potremo avere dati ancora più frequenti e diversificati. Immagino un futuro in cui potremo integrare dati da diverse fonti (misure a terra, dati satellitari, misure in foro) per avere un quadro ancora più completo, dalla superficie fino agli strati rocciosi profondi.

Questo richiederà metodi più sofisticati per l’elaborazione e la fusione dei dati, magari sfruttando il calcolo parallelo o distribuito per ottimizzare l’efficienza degli algoritmi. Ma la strada è tracciata: usare i dati reali per rendere i nostri modelli predittivi sempre più intelligenti e adattivi è la chiave per convivere in modo più sicuro e sostenibile con le attività di estrazione mineraria.

Questo modello è particolarmente utile proprio in quei progetti dove la protezione di strutture importanti richiede già un monitoraggio ad alta frequenza. In questi casi, i dati necessari sono già lì, pronti per essere usati per rendere le previsioni dinamiche a breve termine molto più affidabili.

Fonte: Springer