Oceani Sotto la Lente: Sveliamo la Gravità Marina in 3D ad Altissima Risoluzione!

Ciao a tutti! Oggi voglio portarvi in un viaggio affascinante nel cuore degli oceani, ma non per esplorare creature marine o relitti sommersi. No, oggi parliamo di qualcosa di invisibile ma potentissimo: la gravità! E più precisamente, di come siamo riusciti a “mapparla” con un dettaglio incredibile sopra i mari usando i dati dei satelliti altimetrici. Sembra fantascienza, vero? Eppure, è proprio quello che abbiamo fatto con la nostra modellazione numerica 3D ad alta risoluzione.

Perché Mappare la Gravità Marina?

Forse vi starete chiedendo: “Ma a che serve conoscere la gravità sopra gli oceani con tanta precisione?”. Beh, è fondamentale per un sacco di cose! Dalla comprensione delle correnti oceaniche (che influenzano il clima) alla geologia dei fondali marini (dove si nascondono risorse e faglie tettoniche), fino al miglioramento dei sistemi di navigazione e alla definizione di un sistema di riferimento altimetrico globale più accurato. L’altimetria radar satellitare, negli ultimi 30 anni, ha fatto passi da gigante, regalandoci modelli della superficie media del mare (MSS – Mean Sea Surface) con precisioni di pochi centimetri e risoluzioni pazzesche (parliamo di 1×1 minuto d’arco, circa 1.8 km all’equatore!). Modelli come il recente DTU21_MSS sono tesori di informazioni. E indovinate un po’? La forma di questa superficie è strettamente legata al campo gravitazionale sottostante.

La Sfida: Dai Dati Satellitari alla Gravità

Ok, abbiamo questi dati fantastici sulla forma della superficie marina. Come li trasformiamo in mappe di gravità? Qui entra in gioco la geodésia, con un problema noto come problema al contorno altimetrico-gravimetrico (AGBVP). Esistono vari approcci per risolverlo. Gruppi di ricerca storici come quelli della Scripps Institution of Oceanography (SIO) e della Technical University of Denmark (DTU) hanno sviluppato metodi basati, rispettivamente, sull’analisi delle pendenze della superficie marina (legate alle deviazioni della verticale) o sull’analisi delle ondulazioni del geoide (la forma teorica che il mare assumerebbe sotto la sola influenza della gravità e della rotazione terrestre). Entrambi, in pratica, usano informazioni geometriche derivate dalla MSS, dopo aver sottratto la cosiddetta topografia dinamica media (MDT), che rappresenta le variazioni di livello dovute a correnti e maree.

Il Nostro Approccio: Modellazione 3D con il Metodo dei Volumi Finiti (FVM)

Noi abbiamo scelto una strada un po’ diversa, forse più “fisica”. Invece di partire dalla geometria, abbiamo affrontato l’AGBVP (nello specifico, quello di terzo tipo) numericamente, usando il Metodo dei Volumi Finiti (FVM). L’idea chiave è questa: combiniamo la posizione 3D precisa della MSS (dal modello DTU21_MSS) con un modello geopotenziale globale (GGM) basato sui dati delle missioni satellitari dedicate alla gravità come GRACE e GOCE (nel nostro caso, il GO_CONS_GCF_2_DIR_R6). Questa combinazione ci fornisce le condizioni al contorno di tipo Dirichlet (cioè, valori noti del potenziale perturbatore) sulla superficie degli oceani.

Un vantaggio? Non abbiamo bisogno di un modello MDT a priori! Il potenziale che calcoliamo sulla MSS, però, contiene del “rumore” tipico dei modelli GGM basati su armoniche sferiche. Qui sta il trucco: applichiamo un sofisticato filtraggio non lineare (basato sul modello di Perona-Malik) a questo potenziale. Questo processo è delicatissimo: deve eliminare il rumore ma preservare i dettagli importanti legati, ad esempio, alle correnti oceaniche. È un po’ come restaurare una foto vecchia e preziosa: togli le macchie ma non i dettagli del volto! Il potenziale filtrato, che include implicitamente l’informazione sulla MDT, diventa il nostro dato di input fondamentale sugli oceani.

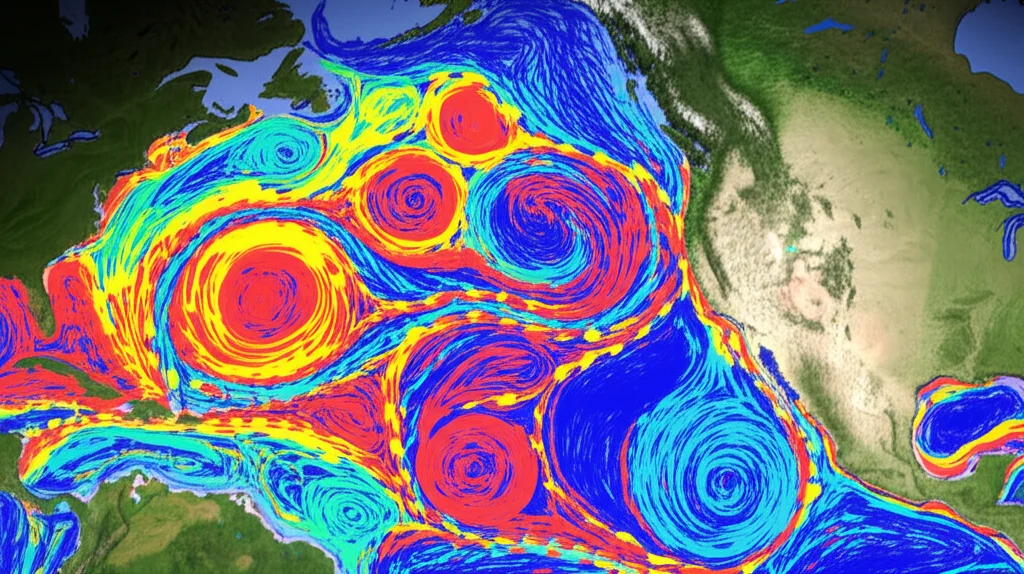
Costruire un Mondo Virtuale (e Pesante!)

Il nostro “laboratorio” è un dominio computazionale 3D che si estende dalla superficie terrestre (approssimata con un ellissoide) fino a 200 km di altitudine. Perché 200 km? È circa l’altezza delle orbite dei satelliti GOCE, e vogliamo “fissare” la nostra soluzione lassù usando i dati del GGM. In pratica, il nostro modello FVM funge da interpolatore 3D basato sulla fisica, che propaga l’informazione gravitazionale dettagliata che abbiamo sulla superficie del mare (grazie all’altimetria) verso l’alto, fino a farla combaciare con l’informazione a larga scala rilevata dai satelliti.

La risoluzione è la chiave: 1×1 minuto d’arco in orizzontale (la stessa dei modelli MSS!) e una divisione non uniforme in verticale (più fitta vicino alla superficie, più rada in quota, per risparmiare risorse). Il risultato? Un mostro computazionale: oltre 93 miliardi di volumi finiti (o incognite)! Gestire una mole di dati del genere richiede potenza di calcolo seria. Abbiamo usato il nostro cluster parallelo, ma anche così, la memoria richiesta (quasi 5 Terabyte!) era troppa. Abbiamo dovuto ricorrere a tecniche di decomposizione del dominio (il metodo di Schwarz additivo), spezzando il problema in sotto-problemi più piccoli e gestibili. Questo ha ridotto drasticamente la memoria (a “solo” 1 GB per sotto-dominio), ma al costo di un tempo di calcolo molto più lungo: circa 30 giorni di CPU time sul nostro cluster! Immaginatevi i computer che frullano giorno e notte…

I Risultati: Non Solo Gravità, Ma Gradienti e Oltre!

Cosa otteniamo dopo tutta questa fatica? Il potenziale perturbatore (la differenza tra il potenziale gravitazionale reale e quello “normale” di un ellissoide ideale) in ogni singolo punto del nostro dominio 3D, con quella risoluzione pazzesca. E da qui, il bello: usando semplici differenze finite, possiamo calcolare numericamente le sue derivate!

• Le derivate prime ci danno le componenti della deviazione della verticale (in orizzontale) e le perturbazioni gravimetriche (gravity disturbances, δg) in verticale. Queste sono le “mappe di gravità” più comuni.
• Le derivate seconde ci danno i gradienti gravimetrici (Txx, Tyy, Tzz, Txy, Txz, Tyz). Questi valori, espressi in Eötvös (E), descrivono come la gravità cambia nello spazio e sono super utili per la geofisica, perché evidenziano strutture geologiche sottili.
• Siamo andati anche oltre, calcolando le derivate terze (Txxx, Tyyy, Tzzz)!

La cosa figa è che otteniamo tutti questi dati non solo sulla superficie del mare (in pratica, sulla MSS DTU21), ma a qualsiasi quota all’interno del nostro dominio 3D, sempre con la risoluzione di 1×1 minuto d’arco.

La Prova del Nove: Confronti e Validazioni

Bello avere tanti dati, ma sono affidabili? Abbiamo fatto diverse verifiche.
Innanzitutto, abbiamo confrontato le nostre perturbazioni gravimetriche sulla superficie del mare con quelle dei dataset più recenti dei gruppi DTU (DTU21_GRAV) e SIO (SS_v31.1). I risultati sono ottimi! Le deviazioni standard delle differenze (residui) sono intorno a 2.7-2.9 mGal (milligal, l’unità di misura della gravità), il che indica un accordo eccellente, specialmente considerando che usiamo approcci diversi. Le differenze maggiori si notano nelle zone polari (dove l’MDT è più incerto) e lungo le coste o le grandi correnti oceaniche, probabilmente a causa delle diverse strategie di gestione dell’MDT e del nostro processo di filtraggio vicino alla terraferma, che può introdurre qualche piccola discrepanza.

Poi, abbiamo usato dati indipendenti: misure di gravità raccolte da navi oceanografiche (dati BGI) e da aerei (campagna GRAV-D negli USA). Anche qui, i confronti sono incoraggianti. Con i dati navali, vediamo che il nostro modello si comporta in modo simile agli altri, anche se emergono le difficoltà vicino alle coste complesse (come nelle Antille) dove il rumore del GGM era alto e il nostro filtraggio ha faticato di più.

Il test con i dati aerei GRAV-D è stato particolarmente interessante, perché ci ha permesso di validare i nostri risultati a diverse altitudini (tra 5 e 11 km). Abbiamo interpolato i nostri valori alle posizioni 3D esatte delle misure aeree. La deviazione standard dei residui è risultata essere intorno ai 3 mGal. Considerando che questa è più o meno l’accuratezza delle misure aeree stesse, è un risultato fantastico! Dimostra che il nostro modello 3D funziona bene anche in quota. Anzi, i nostri dati sono così dettagliati che ci hanno permesso di individuare possibili bias in alcune linee di volo dei dati GRAV-D.

Conclusioni e Prospettive Future

Insomma, il nostro approccio FVM per risolvere l’AGBVP in 3D si è dimostrato capace di produrre dati di gravità marina ad altissima risoluzione (1×1 arc min) e di qualità comparabile ai migliori dataset esistenti, con il vantaggio aggiunto di fornire l’intero campo perturbatore (e le sue derivate di ordine superiore) in un dominio tridimensionale. Il punto chiave è stato il trattamento delle condizioni al contorno oceaniche tramite il filtraggio non lineare del potenziale sulla MSS combinato con un GGM satellitare, che evita l’uso di modelli MDT esterni a priori.

Certo, ci sono margini di miglioramento. Il trattamento delle zone costiere, dove il rumore GGM può essere elevato, necessita di affinamenti, magari integrando informazioni da modelli MDT ibridi o affinando localmente i parametri del filtro. E poi, sognando in grande, con accesso a supercomputer ancora più potenti, potremmo aumentare ulteriormente la risoluzione o passare al Metodo degli Elementi Finiti (FEM) lavorando direttamente sulla geometria reale della MSS, eliminando l’approssimazione ellissoidale.

Ma già così, siamo entusiasti! Fornire gradienti gravimetrici e derivate terze con questa risoluzione e copertura è qualcosa di nuovo. Speriamo che questi dati dettagliatissimi possano aprire nuove strade nella geofisica, nell’oceanografia e nella geodesia, aiutandoci a capire ancora meglio il nostro meraviglioso e complesso pianeta. È stato un lavoro computazionalmente intenso, ma vedere i risultati e le loro potenzialità ripaga di ogni sforzo!

Fonte: Springer