Onde Guidate: Sveliamo i Segreti della Propagazione con un Nuovo Metodo Rivoluzionario!

Ciao a tutti, appassionati di scienza e tecnologia! Oggi voglio parlarvi di qualcosa che, a prima vista, potrebbe sembrare roba da cervelloni chiusi in laboratorio, ma che in realtà ha implicazioni affascinanti e super utili nella vita di tutti i giorni: le onde guidate e come riusciamo a capirci qualcosa di più grazie a un nuovo approccio combinato che definirei quasi “furbo”.

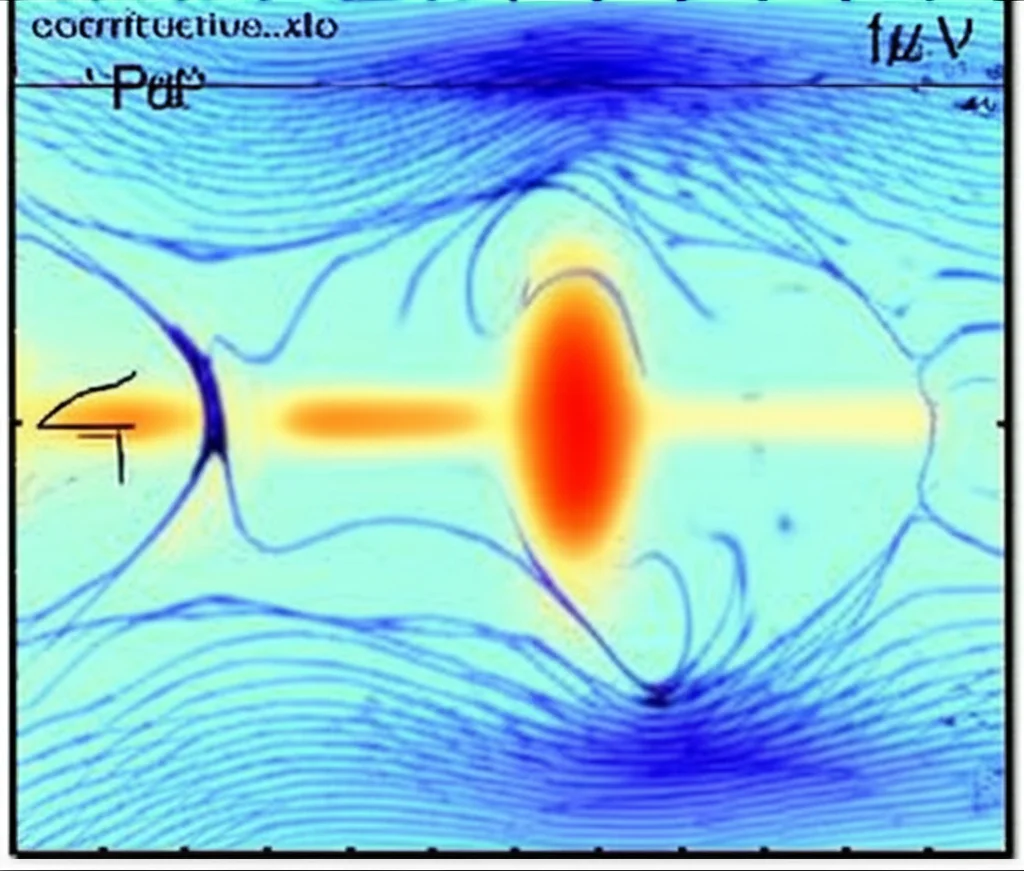
Immaginate di dover “vedere” all’interno di una struttura, come un tubo, una rotaia ferroviaria o persino la carlinga di un aereo, per scovare eventuali difetti o cricche senza doverla smontare o rompere. Ecco, i test non distruttivi (NDT) servono proprio a questo, e una delle tecniche più promettenti sfrutta le cosiddette onde guidate. Queste onde sono un po’ speciali: si propagano lungo una struttura “confinata” (la nostra guida d’onda, appunto), rimanendo parallele ai suoi bordi. Il bello è che possono viaggiare per lunghe distanze con poca attenuazione, il che le rende perfette per ispezionare ampie porzioni di materiale.

Il Labirinto delle Curve di Dispersione

Però, c’è un “ma”. Le onde guidate sono un po’ capricciose: presentano proprietà di dispersione (la loro velocità dipende dalla frequenza, un po’ come la luce in un prisma) e sono multi-modali (possono esistere diverse “forme” d’onda contemporaneamente alla stessa frequenza). Per capire come si comportano queste onde in una data guida d’onda, dobbiamo analizzare le loro curve di dispersione. Queste curve sono dei grafici che ci mostrano, ad esempio, come varia il numero d’onda (legato alla lunghezza d’onda) al variare della frequenza.

Se la guida d’onda ha una forma semplice, tipo una lastra piana, l’analisi si può fare con metodi analitici classici. Ma quando la geometria si complica (pensate a sezioni trasversali arbitrarie), le cose si fanno più toste. Qui entra in gioco il metodo semi-analitico degli elementi finiti (SAFE), uno strumento potentissimo e versatile che ci permette di discretizzare la sezione trasversale della guida e risolvere il problema. Il metodo SAFE è gettonatissimo perché si adatta bene a materiali con caratteristiche complesse, come anisotropia o viscosità.

Tradizionalmente, con il SAFE, si risolve un problema agli autovalori per una frequenza fissata, si ottengono i modi possibili, e poi si ripete per diverse frequenze, cercando di “collegare” i puntini per tracciare le curve. Per capire quale punto appartiene a quale curva, si usano tecniche di “mode sorting”, spesso basate sulla somiglianza delle forme modali (ad esempio, usando il Criterio di Assicurazione Modale o MAC).

Il Problema del “Mode Veering”: Quando le Curve Fanno le Timide

Qui sorge uno dei rompicapi più grossi: il fenomeno del “mode veering”. Immaginate due sentieri di montagna (le nostre curve di dispersione) che si avvicinano tantissimo, quasi a toccarsi, per poi riallontanarsi senza mai incrociarsi veramente. In questi punti, le caratteristiche delle forme modali si “scambiano” tra le due curve. Distinguere un vero incrocio da un “mode veering” diventa un incubo, anche con il MAC, e si rischia di “saltare” da una curva all’altra per errore, ottenendo un tracciamento sbagliato.

Pensate che un incrocio vero e proprio tra curve di dispersione, a meno di simmetrie particolari della struttura, è un evento piuttosto raro. Quindi, il più delle volte, quello che sembra un incrocio è in realtà un “mode veering”. È come se le curve si “respingessero” all’ultimo momento.

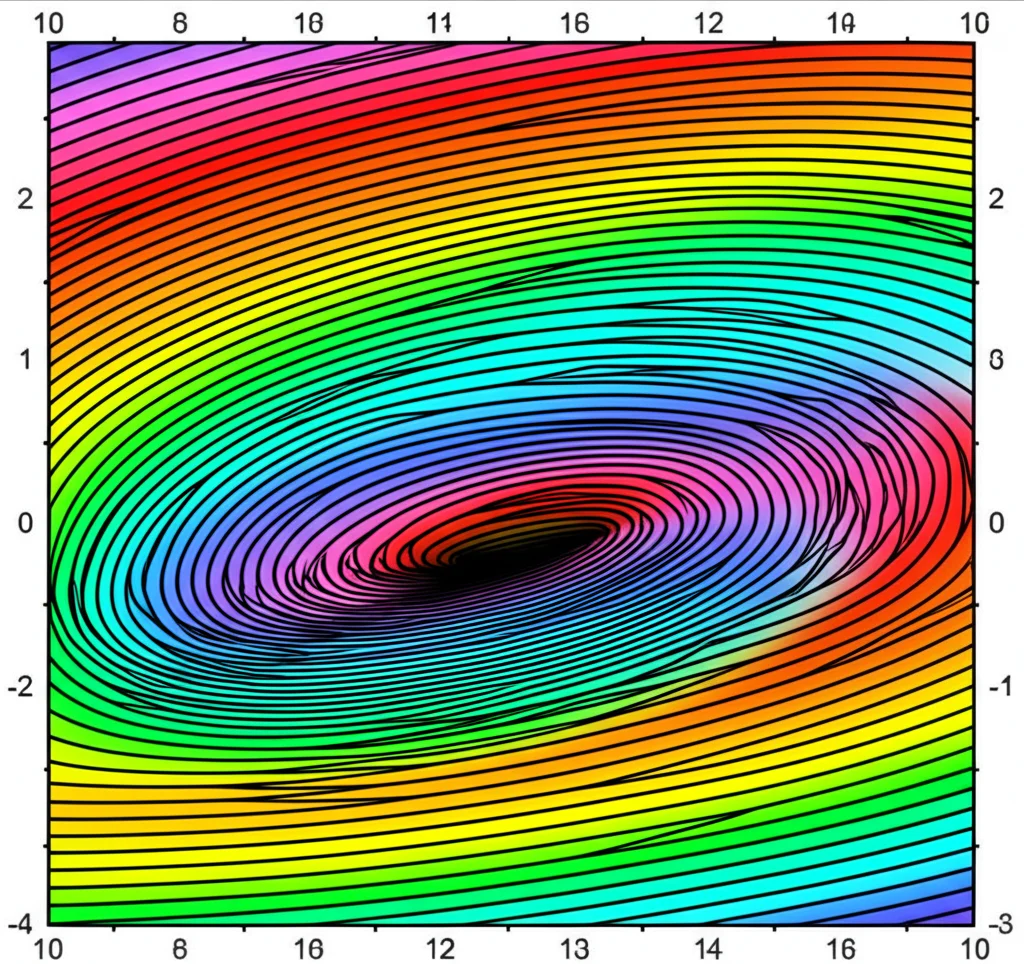
Ed è qui che entra in scena l’approccio di cui vi parlavo all’inizio, una vera e propria svolta presentata in un recente studio. L’idea è quella di combinare il metodo SAFE con un Metodo di Continuazione Numerica (NCM). Invece di risolvere il problema a frequenze discrete e poi “cucire” i risultati, l’NCM permette di tracciare direttamente le curve di dispersione.

La Magia dell’NCM: Tracciare le Curve con Intelligenza

Come funziona? Beh, per prima cosa, il problema agli autovalori quadratico che esce fuori dalla formulazione SAFE viene trasformato in un sistema di equazioni non lineari. Per fare questo, si introducono delle condizioni aggiuntive sulla fase e sull’ampiezza dell’autovettore (che rappresenta la distribuzione della grandezza fisica, tipo lo spostamento, sulla sezione della guida).

La cosa veramente furba è che l’algoritmo NCM non traccia le curve solo sul piano frequenza-numero d’onda, ma in un dominio di parametri più ricco che include anche la struttura modale stessa. Questo significa che l’algoritmo “sa” com’è fatta l’onda mentre la sta tracciando, non lo scopre solo dopo! Di conseguenza, un incrocio che appare tale solo sul piano frequenza-numero d’onda non è un problema, perché nel dominio esteso dell’NCM le strutture modali sono diverse e quindi le curve non si incrociano affatto lì.

Per affrontare il “mode veering” in modo ancora più robusto, i ricercatori hanno introdotto dei vincoli sui vettori tangente e di curvatura delle curve di dispersione. In pratica, l’algoritmo controlla che la curva non faccia “salti” strani o pieghe troppo brusche, tipiche di quando si sta per sbagliare sentiero a causa di un “mode veering”. Se l’algoritmo “sente” che sta per finire sulla curva sbagliata, aggiusta il tiro. È un po’ come avere un navigatore GPS super avanzato per le nostre onde!

Risultati Convincenti e Vantaggi Pratici

I risultati numerici presentati nello studio sono davvero incoraggianti. Hanno testato questo approccio su diversi casi:

• Una lastra stratificata alluminio-acciaio: qui le curve delle onde di Lamb e SH (Shear Horizontal) si incrociano allegramente sul piano frequenza-numero d’onda, ma l’NCM le traccia correttamente perché nel suo dominio di parametri non c’è nessun vero incrocio. Anche i “mode veering”, frequenti in strutture stratificate, vengono gestiti alla grande.
• La stessa lastra, ma considerando anche numeri d’onda immaginari e complessi (che descrivono onde evanescenti o attenuate): anche qui, l’NCM si è dimostrato affidabile.
• Un tubo d’acciaio riempito d’acqua: un caso complesso con molte regioni di “mode veering” a causa della grande differenza di impedenza acustica tra acciaio e acqua. L’NCM ha tracciato le curve in modo robusto, distinguendo anche i modi torsionali che non interagiscono con l’acqua. Hanno persino mostrato come le forme modali si “scambiano” prima e dopo un “mode veering”, mentre un modo torsionale che incrocia una di queste curve mantiene la sua forma inalterata. Affascinante!
• Una barra d’alluminio a forma di L: un esempio di guida d’onda con sezione bidimensionale. Confrontando con un software gratuito (SAFEDC) usato con un passo di campionamento del numero d’onda standard, si vedevano incroci sbagliati dovuti al “mode veering”. L’NCM, invece, ha tracciato tutto correttamente, e i risultati coincidevano con quelli di SAFEDC solo usando un passo di campionamento dieci volte più fine (cosa difficile da sapere a priori!).

Un altro grande vantaggio è che la velocità di gruppo delle onde guidate (che ci dice quanto velocemente si propaga l’energia dell’onda) può essere calcolata facilmente e accuratamente durante il processo di tracciamento NCM, senza calcoli aggiuntivi complessi.

Cosa Ci Riserva il Futuro?

Questo nuovo approccio NCM per il tracciamento delle curve di dispersione è davvero promettente. È più robusto dei metodi convenzionali, soprattutto quando c’è di mezzo il “mode veering”, e adatta automaticamente la “lunghezza del passo” con cui segue la curva, diventando più fitto dove la curva è complessa e più rado dove è semplice. Questo fa risparmiare tempo e migliora l’accuratezza.

La bellezza di questo algoritmo è la sua generalità: potrebbe essere applicato anche ad analisi di dispersione che usano altri metodi numerici (come il BEM, Boundary Element Method), a patto di conoscere certe matrici (Jacobiana e Hessiana, per i più tecnici). Inoltre, si presta benissimo al calcolo parallelo, perché diverse curve di dispersione possono essere tracciate indipendentemente e simultaneamente.

Insomma, anche se la matematica sottostante è complessa (si parla di problemi agli autovalori quadratici, sistemi di equazioni non lineari, metodi predittore-correttore, inversa di Moore-Penrose… un vero spasso per i matematici!), il risultato è un metodo elegante ed efficiente per capire meglio come si propagano le onde guidate. E questo, amici miei, apre la porta a sistemi di ispezione non distruttiva sempre più affidabili e accurati, contribuendo alla sicurezza e alla durabilità delle infrastrutture e dei macchinari che usiamo ogni giorno. Non è fantastico?

Fonte: Springer