Testi Brevi e Cluster Misteriosi: Sveliamo i Segreti con l’Inferenza Variazionale Stocastica!

Ciao a tutti! Oggi voglio parlarvi di una sfida affascinante nel mondo dell’analisi dei dati, in particolare quando abbiamo a che fare con testi brevi. Pensate a tweet, post sui social media, abstract di articoli: piccole gemme di informazione che, messe insieme, formano enormi moli di dati. Come possiamo dare un senso a tutto questo, raggruppando automaticamente testi simili per argomento (un processo chiamato clustering)?

Il Problema: Trovare Argomenti Nascosti nei Testi Brevi

Una tecnica molto usata per analizzare testi è rappresentarli come “Bag-of-Words” (BOW), ovvero un “sacco di parole”. In pratica, per ogni documento, contiamo quante volte appare ciascuna parola di un vocabolario predefinito, ignorando l’ordine. È un po’ come svuotare un libro in un sacco e contare le parole, senza preoccuparsi delle frasi.

Per fare clustering su questi dati, un modello statistico che funziona sorprendentemente bene, soprattutto con testi brevi, è la mistura finita di distribuzioni Dirichlet-Multinomiali. Non spaventatevi per il nome! Immaginate di avere diversi “argomenti” (topic) nascosti nei vostri dati. Ogni argomento è descritto da una distribuzione di probabilità sulle parole del vocabolario (ad esempio, un topic “sport” avrà alte probabilità per parole come “calcio”, “partita”, “squadra”). Il modello assume che ogni documento sia stato generato da *uno* di questi argomenti. La parte “Dirichlet” aggiunge un tocco bayesiano, aiutando a gestire meglio le parole rare e il fenomeno del “word burstiness” (quando una parola, se appare, tende ad apparire più volte nello stesso documento).

Questi modelli Dirichlet-Multinomiali (DMM) sono spesso più efficaci per i testi brevi rispetto a modelli più complessi come la famosa Latent Dirichlet Allocation (LDA), che permette a un documento di trattare più argomenti contemporaneamente. La semplicità del DMM è la sua forza in questo contesto.

L’Approccio Bayesiano e la Sfida Computazionale

Possiamo affrontare questi modelli DMM con un approccio bayesiano. Questo significa che non cerchiamo solo *una* stima dei parametri (le probabilità delle parole per ogni topic e i pesi dei topic), ma un’intera distribuzione di probabilità che rifletta la nostra incertezza. Il problema è che, anche se il modello è relativamente semplice, calcolare esattamente questa distribuzione a posteriori (la distribuzione dei parametri *dopo* aver visto i dati) è matematicamente intrattabile. Un vero rompicapo!

Qui entrano in gioco i metodi numerici. Una strada promettente è l’Inferenza Variazionale (VI). L’idea geniale della VI è approssimare la complicata distribuzione a posteriori con una più semplice, scelta da una famiglia di distribuzioni “trattabili” (spesso assumendo che i parametri siano indipendenti a posteriori, un’assunzione chiamata “mean-field”). Si cerca poi la distribuzione approssimata che sia il più “vicina” possibile a quella vera, misurando la vicinanza con la divergenza di Kullback-Leibler (KL). Massimizzare una quantità chiamata Evidence Lower Bound (ELBO) è equivalente a minimizzare questa divergenza KL.

CAVI: L’Algoritmo Standard (ma Lento)

Un algoritmo comune per l’inferenza variazionale è il Coordinate Ascent Variational Inference (CAVI). Funziona aggiornando iterativamente i parametri della distribuzione approssimata, un pezzo alla volta, fino a convergenza. È come scalare una montagna ottimizzando una coordinata alla volta. CAVI ha dei vantaggi: evita il problema del “label switching” (un fastidio tipico dei metodi MCMC dove le etichette dei cluster si scambiano casualmente) e converge generalmente più in fretta degli MCMC.

Ma c’è un grosso “ma”: ogni iterazione di CAVI richiede di processare l’intero dataset per aggiornare i parametri locali (quelli specifici per ogni documento, come a quale cluster appartiene). Immaginate di avere milioni di tweet: ripassarli tutti ad ogni singolo passo diventa proibitivo! La scalabilità è un problema serio.

La Soluzione Scalabile: Inferenza Variazionale Stocastica (SVI)

Ed ecco che arriva la nostra eroina: l’Inferenza Variazionale Stocastica (SVI)! Introdotta originariamente da Hoffman e colleghi nel 2013, SVI è un adattamento scalabile di CAVI basato sull’ottimizzazione stocastica tramite gradiente.

L’idea chiave è semplice ma potente: invece di usare *tutti* i dati ad ogni iterazione per calcolare l’aggiornamento (il gradiente), SVI ne prende solo uno (o un piccolo batch) a caso! Questo produce una stima “rumorosa” ma imparziale (unbiased) del gradiente. È come cercare la cima della montagna seguendo indicazioni un po’ imprecise ma che, in media, puntano nella direzione giusta.

Questo approccio stocastico ha un impatto enorme sulla scalabilità. Non dobbiamo più caricare e processare l’intero dataset ad ogni passo. Sotto certe condizioni (le cosiddette condizioni di Robbins-Monro sulla dimensione del passo di apprendimento), questo algoritmo “rumoroso” converge comunque a un massimo locale della superficie dell’ELBO.

Come Funziona SVI nel Nostro Modello?

Nel nostro lavoro, abbiamo adattato e generalizzato il framework SVI per il modello di misture Dirichlet-Multinomiali. Abbiamo derivato le equazioni di aggiornamento specifiche, basandoci su assunzioni abbastanza semplici sulla forma delle distribuzioni condizionali complete del modello e delle distribuzioni variazionali (devono appartenere alla famiglia esponenziale).

In pratica, l’algoritmo SVI funziona così:

• Seleziona casualmente un documento dal corpus.
• Usa solo quel documento per calcolare una stima rumorosa di come aggiornare i parametri globali del modello (le probabilità delle parole per ogni topic (pmb{{mathbb{B}}}) e i pesi dei topic (pmb{lambda})).
• Aggiorna i parametri globali facendo un piccolo passo nella direzione indicata da questa stima rumorosa (usando un tasso di apprendimento (rho^{(t)}) che decresce nel tempo).
• Aggiorna il parametro locale solo per quel documento selezionato (la probabilità che appartenga a ciascun cluster (pmb{gamma}_i)).
• Ripeti il processo molte volte.

Questo ciclo è incredibilmente più efficiente per ogni iterazione rispetto a CAVI.

SVI vs CAVI: La Prova sul Campo

Abbiamo messo alla prova SVI confrontandolo con CAVI su diversi compiti di clustering di testi. Abbiamo usato dataset reali come sottoinsiemi della famosa collezione Reuters 21578 e il dataset BBCSport. Abbiamo misurato:

• Tempo di calcolo: Quanto ci mettono gli algoritmi a convergere?
• Accuratezza del clustering: Quanto bene i cluster trovati corrispondono alle categorie reali (usando misure come l’Adjusted Rand Index – ARI e l’accuratezza permutata)?
• Qualità dei topic: I topic trovati sono semanticamente coerenti e interpretabili?
• Selezione del modello: Come si comportano gli algoritmi quando devono scegliere il numero giusto di cluster (k)?

I risultati sono stati davvero interessanti!

Velocità: Come previsto, SVI è molto più veloce *per iterazione* (da 2 a 3.5 volte più veloce di CAVI nei nostri esperimenti). Tuttavia, SVI richiede generalmente *più iterazioni* per convergere a causa della natura rumorosa degli aggiornamenti. Nonostante ciò, per dataset di medie dimensioni, il vantaggio di scalabilità rende SVI computazionalmente fattibile.

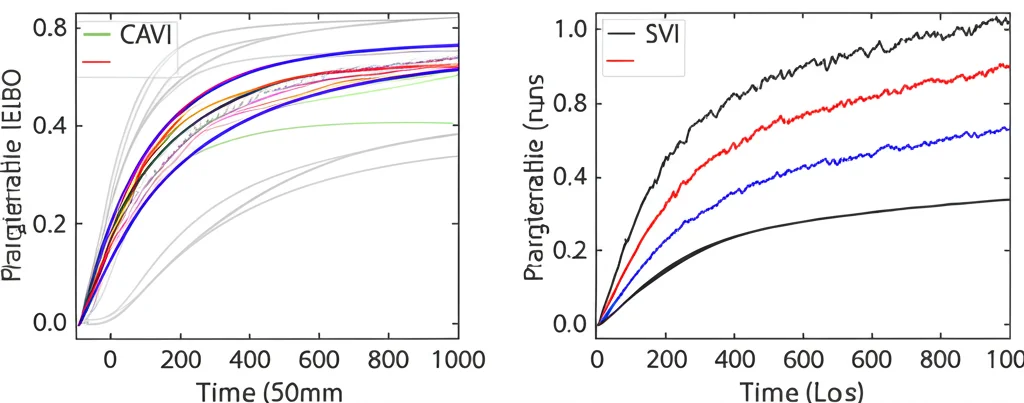
Qualità della Soluzione: Qui arriva la sorpresa. Anche se SVI esplora meno “modi” (massimi locali) della superficie approssimata rispetto a CAVI a parità di numero di run, abbiamo osservato che SVI tende a trovare soluzioni di qualità superiore! In diversi esperimenti, SVI ha raggiunto un’accuratezza di clustering (ARI e Acc) significativamente più alta rispetto a CAVI, a volte anche con meno run totali (anche se ogni run SVI richiede più iterazioni). Sembra che la “rumorosità” di SVI lo aiuti a sfuggire a massimi locali subottimali dove CAVI potrebbe rimanere intrappolato.

Regolarizzazione Implicita e Coerenza dei Topic: Abbiamo anche notato un fenomeno affascinante con il dataset BBCSport, dove le categorie sportive sono semanticamente vicine. CAVI tendeva a produrre topic un po’ confusi. SVI, invece, non solo ha prodotto topic più interpretabili per alcune categorie, ma ha anche mostrato una sorta di “regolarizzazione implicita“. Quando abbiamo impostato k=5 (il numero reale di categorie), SVI ha assegnato pesi quasi nulli a uno o due componenti, suggerendo che un modello con meno cluster sarebbe stato più appropriato per quei dati. Abbiamo verificato questo usando misure di coerenza dei topic (come quella di Mimno et al.), che hanno confermato che i componenti “svuotati” da SVI erano effettivamente di bassa qualità. Questo suggerisce che SVI potrebbe essere più robusto quando il numero di cluster scelto è troppo alto.

Selezione del Modello: Abbiamo testato come CAVI e SVI si comportano nella scelta del numero di cluster (k) usando il criterio BIC (Bayesian Information Criterion) su dati sintetici derivati da BBCSport. Entrambi gli algoritmi tendono a sottostimare k (un comportamento noto del BIC con le misture), ma SVI sembra farlo in modo più marcato, preferendo modelli più semplici, in linea con l’effetto di regolarizzazione osservato.

Conclusioni e Prossimi Passi

L’inferenza variazionale stocastica (SVI) si dimostra uno strumento davvero promettente per il clustering di testi brevi con misture Dirichlet-Multinomiali. Offre vantaggi significativi in termini di scalabilità rispetto a CAVI, rendendo fattibile l’analisi di dataset più grandi. Ma la cosa forse più eccitante è che sembra portare a soluzioni di qualità superiore, sia in termini di accuratezza che di interpretabilità dei topic, mostrando anche una potenziale capacità di regolarizzazione implicita.

Certo, c’è ancora lavoro da fare. La convergenza di SVI può essere lenta, e per corpora veramente massicci (milioni di documenti), potrebbero servire ulteriori ottimizzazioni (come evitare il calcolo dell’ELBO ad ogni iterazione, vettorizzare gli aggiornamenti, o esplorare approcci distribuiti/online).

Inoltre, potremmo esplorare modelli più flessibili. Ad esempio, usare priori diversi per i pesi dei topic (come il Logistic-Normal o il Beta-Liouville) potrebbe catturare meglio le correlazioni tra argomenti, anche se complica l’inferenza.

In definitiva, SVI apre nuove porte per analizzare l’enorme flusso di testi brevi che generiamo ogni giorno. È un’area di ricerca attiva e affascinante, e non vedo l’ora di vedere dove ci porteranno i prossimi sviluppi!

Fonte: Springer