Ponti che Tremano e Producono Energia? La Magia Piezoelettrica e il Segreto delle Vibrazioni Non Lineari!

Ciao a tutti, appassionati di scienza e curiosi! Oggi voglio portarvi con me in un viaggio affascinante, al confine tra ingegneria civile, fisica dei materiali e un pizzico di… magia tecnologica. Avete mai pensato che un ponte, oltre a farci attraversare fiumi e valli, potesse diventare una mini-centrale elettrica? Sembra fantascienza, vero? Eppure, è proprio quello di cui parleremo: come sfruttare le vibrazioni dei ponti ferroviari per produrre energia pulita, grazie a materiali speciali chiamati piezoelettrici. E la parte più intrigante? Andremo a scoprire come certi “comportamenti bizzarri” di queste vibrazioni, noti come nonlinearità geometriche, potrebbero darci una marcia in più!

Perché Tanta Fatica per un po’ di Energia?

Vi chiederete: perché scomodarsi tanto? Beh, pensate ai moderni sistemi di monitoraggio della salute strutturale (SHM). I nostri ponti sono sempre più “intelligenti”, pieni di sensori che ne controllano lo stato, la sicurezza, e comunicano dati tramite Wi-Fi. Tutta questa tecnologia ha bisogno di energia. Tradizionalmente, si usano batterie elettrochimiche. Ma qui casca l’asino: le batterie si scaricano, vanno ricaricate o sostituite (immaginate la scomodità su strutture difficilmente accessibili!), e non sono esattamente il top in termini di sostenibilità. Ed è qui che entrano in gioco i nostri amici piezoelettrici.

Il Superpotere Piezoelettrico: Energia dalle Deformazioni

I materiali piezoelettrici hanno una proprietà quasi magica: se li deformi meccanicamente (li schiacci, li pieghi), generano una tensione elettrica. Viceversa, se applichi loro una tensione, si deformano. Fantastico, no? Questo li rende candidati ideali per creare dei dispositivi, chiamati “energy harvesters” (raccoglitori di energia), capaci di catturare l’energia residua delle vibrazioni meccaniche presenti in ogni struttura. Certo, non parliamo di quantità di energia da alimentare una città, ma abbastanza per far funzionare quei sensori di cui parlavamo, rendendoli autonomi e più “green”.

Nel contesto dei ponti ferroviari, gli approcci principali sono due:

• Patch adesive attaccate alla struttura: spesso fatte di polimeri, che però hanno un’efficienza di conversione energetica inferiore rispetto alle ceramiche.
• Harvester a sbalzo (cantilever): una sorta di trampolino con una massa all’estremità per “sintonizzarlo” e una o più ceramiche piezoelettriche. Molti studi, finora, si sono concentrati su piccole deformazioni, in regime lineare.

Ma cosa succede se le deformazioni diventano… importanti? Qui entra in gioco la nonlinearità geometrica. Alcuni studi hanno suggerito che questa nonlinearità diventa significativa con livelli di eccitazione di base tra 1.5 e 2 [g] (g è l’accelerazione di gravità) e che può aumentare la potenza raccolta quando lo spostamento della punta della trave supera il 30% della sua lunghezza. Insomma, c’è del potenziale inesplorato!

Il Nostro Studio: Un Mix di Esperimenti, Teoria e Numeri

Ed eccoci al cuore del nostro lavoro. Abbiamo voluto vederci chiaro, combinando dati sperimentali, modelli teorici e simulazioni numeriche per progettare un harvester vibrante specifico per i ponti ferroviari. Il nostro dispositivo è una trave in alluminio rivestita (per proteggerla dagli agenti atmosferici) con un materiale piezoelettrico chiamato PZT-5J. La vera novità? Abbiamo studiato a fondo il contributo delle vibrazioni geometricamente non lineari alla tensione prodotta.

Per fare le cose per bene, abbiamo usato uno strumento probabilistico che integra il metodo degli elementi finiti (FE) – un potente strumento di simulazione – e le tecniche Monte Carlo, per tenere conto delle inevitabili incertezze presenti nelle misure sperimentali. Immaginatelo come un modo per fare migliaia di “esperimenti virtuali” cambiando leggermente i parametri, per vedere quanto robusti sono i nostri risultati.

Ecco i passi che abbiamo seguito:

1. Abbiamo determinato le proprietà elastiche della trave usando tecniche non distruttive a ultrasuoni (un po’ come un’ecografia per materiali!).
2. Abbiamo calcolato la lunghezza della trave con un’analisi modale probabilistica per “sintonizzarla” sulla frequenza tipica di un ponte ferroviario di medie dimensioni (circa 3.26 Hz, secondo gli Eurocodici per ponti con campate tra 30 e 100 metri).
3. Abbiamo ottenuto lo smorzamento e i picchi non lineari nel dominio della frequenza combinando misure sperimentali di vibrazione libera con risultati lineari e non lineari dalle simulazioni.
4. Infine, abbiamo misurato la tensione di uscita a varie ampiezze di eccitazione di base, sia per i picchi lineari che non lineari, per capire l’impatto della nonlinearità geometrica.

Un dettaglio importante: nel nostro studio sperimentale, abbiamo usato un harvester uni-morfico (un solo piezoelettrico) e senza una massa aggiuntiva sulla punta, per ridurre le incertezze. Il piezoelettrico PZT-5J è stato scelto per le sue buone proprietà e la stabilità alle variazioni di temperatura, cruciale per un’applicazione su un ponte.

Dentro la Fisica: Equazioni Lineari e Non Lineari

Senza addentrarci troppo nei dettagli matematici (che possono essere un po’ ostici!), le equazioni che governano la piezoelettricità accoppiano l’energia meccanica ed elettrica. Per la parte meccanica, abbiamo considerato sia il modello lineare (piccole deformazioni) sia un modello che include le nonlinearità geometriche (il modello di Saint-Venant-Kirchhoff, o SVK). Quest’ultimo aggiunge un termine quadratico nelle deformazioni, che è proprio quello che “cattura” il comportamento non lineare quando la trave si piega molto. Entrambi i modelli sono stati implementati nel software FE COMSOL Multiphysics^ecopy;.

Per la parte probabilistica, abbiamo associato a ogni variabile casuale (come le proprietà del materiale, le dimensioni, ecc.) una funzione di distribuzione (Gaussiana se conoscevamo media e deviazione standard, uniforme se avevamo un intervallo). Poi, con la tecnica del Latin Hypercube, abbiamo generato un campione rappresentativo di queste variabili e lanciato le simulazioni per ognuna, ottenendo così una “nuvola” di risultati che ci ha permesso di calcolare media e deviazione standard dell’output (ad esempio, la tensione).

Gli Esperimenti: Ultrasuoni e Vibrazioni Controllate

Abbiamo allestito due setup sperimentali principali:

• Caratterizzazione non distruttiva: Con un rilevatore di difetti a ultrasuoni OLYMPUS Epoch 650 e due tipi di trasduttori piezoelettrici, abbiamo generato onde di taglio e di pressione attraverso la nostra trave. Misurando il tempo che queste onde impiegavano ad attraversare lo spessore, abbiamo potuto calcolare il modulo di Young e il coefficiente di Poisson dell’alluminio rivestito. Questi valori sono risultati coerenti con quelli noti in letteratura.
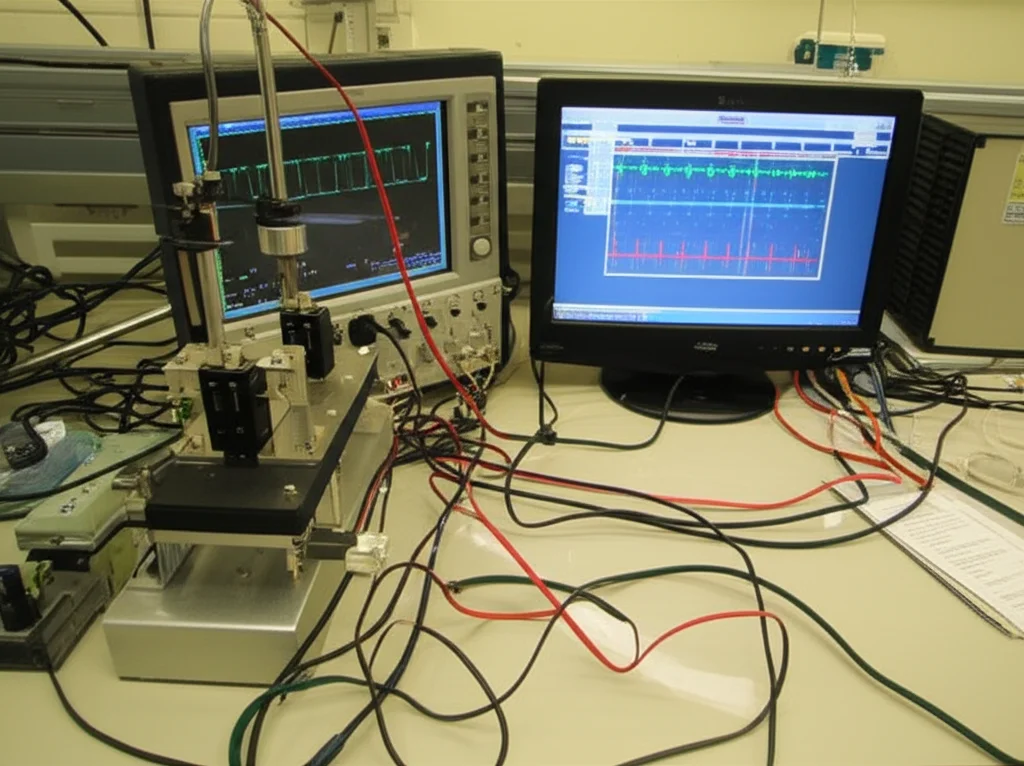
• Setup dinamico: Qui abbiamo montato la nostra trave in alluminio su uno strumento di vibrazione meccanica (ElectroForce 3520). Abbiamo usato un estensimetro per misurare la deformazione vicino all’incastro (dove poi avremmo messo il piezoelettrico) e un oscilloscopio Agilent per registrare la tensione generata dal piezoelettrico. Questo ci ha permesso di studiare sia le vibrazioni libere (dando una “botta” iniziale alla trave e lasciandola vibrare) sia quelle forzate (imponendo una vibrazione di base simile a quella di un ponte al passaggio di un treno).

Risultati Che Fanno Scintille (o Quasi!): Cosa Abbiamo Visto?

E ora, i risultati! Li abbiamo divisi in “casi” per chiarezza.

Caso I – Analisi Modale: L’obiettivo era calcolare la lunghezza della trave per sintonizzarla a 3.26 Hz. I risultati numerici (sia con modello lineare che SVK, che in questo caso danno lo stesso risultato perché non ci sono stress residui) e quelli teorici (basati sulla teoria della trave di Eulero-Bernoulli) sono stati in ottimo accordo.

Caso II – Vibrazione Libera: Abbiamo spostato l’estremità libera della trave di circa 10 cm e l’abbiamo lasciata vibrare, misurando la deformazione nel tempo. Trasformando il segnale nel dominio della frequenza con una FFT (Trasformata Rapida di Fourier), abbiamo visto chiaramente la frequenza principale a 3.26 Hz e una seconda a 20.48 Hz, vicinissima a quella calcolata dalle simulazioni. Ma la cosa più interessante è che abbiamo osservato anche armoniche non lineari a 6.56 Hz e 9.75 Hz nei dati sperimentali, e a 6.53 Hz e 9.65 Hz nelle simulazioni con il modello SVK. Queste non erano presenti nel modello lineare! Bingo! La nonlinearità geometrica c’era e produceva un “indurimento” della trave.
Abbiamo anche calcolato lo smorzamento della trave (circa 1.38%), un fattore cruciale perché, come sospettavamo, uno smorzamento elevato può “mascherare” i picchi di frequenza dovuti alla nonlinearità. Le nostre simulazioni lo hanno confermato: aumentando lo smorzamento numerico, il picco non lineare diventava invisibile.

Caso III – Vibrazione Forzata (e Produzione di Energia!): Qui abbiamo tolto l’estensimetro e messo il nostro PZT-5J. Abbiamo imposto una vibrazione di base con ampiezza di 30 mm e frequenza di 3.26 Hz. Ebbene, al picco lineare (risonanza a 3.26 Hz), abbiamo misurato una tensione di ben 72.23 Volt! Un valore notevole, per darvi un’idea, due ordini di grandezza superiore a quanto riportato in altri studi su harvester stampati in 3D per ponti ferroviari.
E le risposte non lineari? Abbiamo osservato due picchi:

• Attorno a 6.53 Hz, con una tensione di 0.19 V (circa lo 0.3% della produzione totale).
• Attorno a 9.78 Hz, con una tensione di 0.14 V (circa lo 0.2% della produzione totale).

Piccole, vero? Ma non è finita qui. Abbiamo variato l’ampiezza della vibrazione di base da 5 a 100 mm, mantenendo la frequenza a 3.26 Hz. Per la prima armonica non lineare, la tensione generata aumentava quasi linearmente con l’ampiezza, arrivando allo 0.4% per 100 mm. Ma per la seconda armonica non lineare, la curva di tensione si adattava splendidamente a una funzione quadratica! E il contributo non lineare saliva allo 0.7%. Questo è super interessante!

Conclusioni: Un Futuro Energetico per i Nostri Ponti?

Cosa ci portiamo a casa da tutto questo?

1. La tecnica non distruttiva a ultrasuoni si è rivelata affidabile per caratterizzare i materiali rivestiti e sintonizzare l’harvester. Ottimo per progetti futuri!
2. Le vibrazioni geometricamente non lineari sono state osservate sperimentalmente e confermate numericamente. Non erano solo un’ipotesi teorica!
3. Lo smorzamento gioca un ruolo chiave e va considerato attentamente, specialmente se si vogliono sfruttare gli effetti non lineari.
4. Il nostro harvester può generare una tensione significativa (72.23 V) in condizioni di risonanza lineare.
5. Il contributo non lineare alla tensione, nelle condizioni operative tipiche testate, è risultato piccolo (meno dell’1%).

Ma l’ultima scoperta è la più promettente: la produzione di energia che aumenta quadraticamente con la seconda armonica non lineare. Questo suggerisce che, se riuscissimo a progettare harvester che lavorano in regimi di maggiore ampiezza di spostamento, o se trovassimo modi per amplificare queste vibrazioni, potremmo davvero sfruttare la nonlinearità per ottenere un bel boost di energia!

Insomma, la strada per ponti che non solo ci sostengono ma si auto-alimentano (almeno per i loro sensori) è tracciata. La ricerca futura dovrà concentrarsi sull’ottimizzazione del design degli harvester per esaltare questi effetti non lineari. Chissà, magari un giorno ogni ponte sarà una piccola, silenziosa e verde fonte di energia. Io ci spero!

Fonte: Springer