Griglie di Interpolazione Veloce per Drell-Yan: Decifrare il Protone a Tempo di Record!

Ragazzi, parliamoci chiaro: capire cosa succede quando le particelle si scontrano a energie pazzesche come quelle raggiunte all’LHC (Large Hadron Collider) è una sfida enorme, ma assolutamente affascinante! Le analisi moderne dei dati sperimentali richiedono previsioni teoriche incredibilmente precise, spinte a ordini di accuratezza elevatissimi nella cosiddetta teoria perturbativa (QCD perturbativa o pQCD), come il livello NNLO (Next-to-Next-to-Leading Order) e oltre. Il problema? Questi calcoli sono dei veri e propri “mostri” computazionali, richiedono risorse enormi e tantissimo tempo.

La Sfida: Calcoli Complessi e la Necessità di Flessibilità

Immaginate di dover fare questi calcoli complicatissimi e poi, magari, voler vedere cosa succede cambiando leggermente le “carte d’identità” delle particelle iniziali (le famose Funzioni di Distribuzione Partonca, o PDF) o le scale di energia in gioco. Tradizionalmente, questo significherebbe rifare gran parte del calcolo da capo. Una follia, soprattutto quando si devono testare decine o centinaia di scenari diversi, come accade quando si cerca di determinare con precisione la struttura interna del protone (i cosiddetti “fit” delle PDF).

Qui entra in gioco uno strumento geniale: le griglie di interpolazione veloce. Pensatele come delle mappe super-dettagliate e pre-calcolate che “memorizzano” i risultati dei calcoli complessi in modo intelligente. Una volta creata la griglia, valutare una previsione teorica con nuove PDF o nuove scale diventa quasi istantaneo! Librerie come APPLgrid, fastNLO e la più recente `pineappl` sono state sviluppate proprio per questo scopo.

Il Pezzo Mancante: Drell-Yan a NNLO

Negli anni, sono state create griglie a NNLO per molti processi importanti: la produzione di jet in urti profondamente inelastici (DIS), la produzione di jet negli scontri tra adroni (come all’LHC), la produzione di coppie di quark top e persino il DIS inclusivo. Ma mancava un pezzo da novanta: il processo di Drell–Yan (DY).

Il processo Drell-Yan, che descrive la produzione di bosoni elettrodeboli (come W e Z) negli scontri tra adroni, è fondamentale. Fornisce vincoli importantissimi sulla quantità di quark dentro al protone e rappresenta circa il 20% dei dati usati nei fit globali più recenti delle PDF! Nonostante le previsioni teoriche per il DY a NNLO fossero disponibili da tempo (e recentemente si sia arrivati addirittura a N³LO!), non esistevano griglie differenziali a NNLO. Questo costringeva i fisici a usare un’approssimazione: griglie NLO (meno precise) “corrette” con dei fattori (i K-factor) calcolati a NNLO solo per una specifica PDF. Non proprio l’ideale per studi di altissima precisione.

La Nostra Soluzione: Un Ponte tra NNLOjet e pineappl

Per colmare questa lacuna, abbiamo sviluppato una nuova interfaccia tra il generatore Monte Carlo a livello partonico NNLOjet (basato sul sofisticato formalismo della sottrazione ad antenna) e la libreria di interpolazione pineappl. Questo “ponte” ci permette ora di produrre griglie di interpolazione per tutti i processi inclusi in NNLOjet, e lo abbiamo subito messo alla prova proprio con il nostro amato Drell-Yan!

E la notizia ancora migliore? Insieme a questo lavoro, abbiamo reso pubbliche un’ampia gamma di griglie per il Drell-Yan, coprendo praticamente tutti i dati sperimentali del Tevatron e dell’LHC che vengono comunemente usati nei fit globali delle PDF (come quelli per NNPDF4.0). Potete scaricarle e iniziare a giocarci! (Trovate il link alla fine).

Come Funzionano e Cosa Contengono le Griglie

L’idea di base delle griglie sfrutta la fattorizzazione QCD: la sezione d’urto adronica (quello che misuriamo) può essere scritta come una convoluzione (una specie di “media pesata”) tra la sezione d’urto partonica (il calcolo teorico fondamentale) e le PDF. Le griglie pre-calcolano questa convoluzione usando delle funzioni base per le PDF. Quando poi volete il risultato per una PDF specifica, basta fare una somma veloce dei valori sulla griglia, pesati con la vostra PDF. Un risparmio di tempo enorme!

Le griglie che abbiamo rilasciato contengono un sacco di informazioni utili (metadati), accessibili tramite l’interfaccia a riga di comando (CLI) di `pineappl`:

• La configurazione usata per generare la griglia (runcard).
• Le versioni specifiche di NNLOjet e pineappl utilizzate.
• I risultati di riferimento del calcolo originale, con gli errori statistici.
• La PDF usata per generare i risultati di riferimento (utile per i test).
• Il riferimento ai dati sperimentali su HEPData.

Un vantaggio chiave è che queste griglie occupano relativamente poco spazio su disco, a differenza di altri approcci che salvano ogni singolo evento di collisione. Certo, si perde un po’ di flessibilità (la configurazione dell’analisi è fissata), ma il guadagno in velocità e spazio è impagabile.

Test di Affidabilità: Quanto sono Precise?

Ovviamente, ci siamo chiesti: l’interpolazione introduce errori significativi? Specialmente per il Drell-Yan a NNLO, dove le correzioni sono piccole e ci sono grandi cancellazioni numeriche, la precisione è fondamentale. Abbiamo fatto dei “closure test”, confrontando i risultati ottenuti dalle griglie con i calcoli esatti originali.

I risultati sono ottimi! Gli errori dovuti all’interpolazione sono tipicamente ben al di sotto del per mille nella maggior parte dello spazio delle fasi. Solo in casi estremi (come nelle regioni molto “forward” dell’esperimento LHCb) possono arrivare a qualche per mille. Ma attenzione: stiamo parlando di errori sulla *correzione* NNLO, che è già piccola di suo. L’impatto sul risultato finale è a livello dello 0.01‰, completamente trascurabile rispetto agli errori statistici del calcolo originale e, soprattutto, rispetto alle incertezze sperimentali. Quindi, state tranquilli: per qualsiasi applicazione fenomenologica, queste griglie sono super-affidabili!

Cosa Possiamo Fare con Queste Griglie? Esempi Pratici

Uno degli usi più comuni è lo studio delle incertezze teoriche. Ad esempio, come cambiano le previsioni se variamo le scale di rinormalizzazione e fattorizzazione ((mu_R) e (mu_F))? Questo ci dà una stima dell’impatto degli ordini perturbativi che non abbiamo ancora calcolato. Con le griglie e la CLI di `pineappl`, possiamo esplorare lo spazio ((mu_R, mu_F)) con grande dettaglio e ottenere le classiche “variazioni a 9 punti” (fattori 1/2, 1, 2 per entrambe le scale) con un semplice comando.

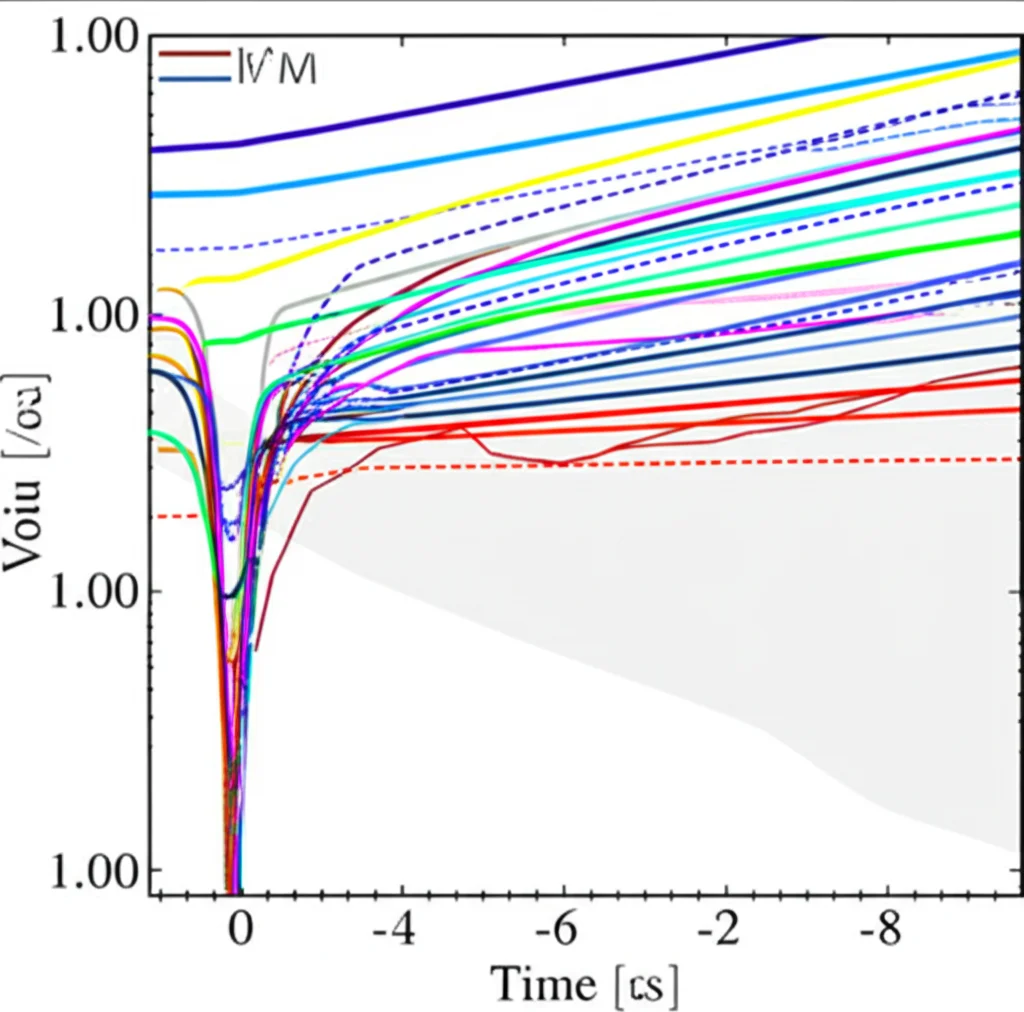
Un altro uso cruciale è lo studio delle incertezze legate alle PDF. Le PDF non sono conosciute perfettamente, ma vengono fornite come un set di “repliche” che rappresentano la loro incertezza. Le griglie permettono di ricalcolare la sezione d’urto per ognuna di queste repliche (e per diversi set di PDF da gruppi differenti come MHST, CTEQ, NNPDF) in pochi secondi! Questo è vitale sia per stimare l’incertezza totale delle previsioni, sia per usare queste previsioni all’interno dei fit globali per determinare le PDF stesse. La CLI permette anche di confrontare direttamente le previsioni e le incertezze ottenute con diversi set di PDF, generando grafici chiari e informativi.

Uno Sguardo Approfondito: Le Misteriose Cancellazioni nel Drell-Yan

Il processo Drell-Yan a NNLO ha una caratteristica peculiare che ha fatto discutere parecchio: delle grandi cancellazioni “accidentali” tra i contributi dei diversi canali partonici (ad esempio, quark-antiquark contro quark-gluone). Queste cancellazioni sono così forti che a volte le incertezze di scala stimate a NNLO sembrano sottostimate, tanto che le previsioni N³LO (più precise) cadono fuori da queste bande di incertezza! Sembrava che queste cancellazioni fossero legate a correlazioni tra i gluoni e i quark del “mare”.

Le griglie ci hanno offerto un’opportunità unica per investigare questo fenomeno. Possiamo usarle per valutare i contributi dei singoli canali partonici separatamente e vedere come cambiano al variare della scala di fattorizzazione (mu_F). Abbiamo osservato che la cancellazione tra i canali (qbar{q}) e ((qg + bar{q}g)) è enorme, quasi due ordini di grandezza attorno alla massa dello Z! E dipende fortemente da (mu_F).

Per capirci di più, abbiamo cambiato “base”, passando dalla base di sapore (quark su, giù, strano…) alla cosiddetta “base di evoluzione”, che disaccoppia l’evoluzione dei diversi componenti secondo le equazioni DGLAP. In questa nuova base, magia! Le cancellazioni sono molto meno pronunciate e la dipendenza dalla scala (mu_F) diventa quasi piatta. Questo dimostra che gran parte delle cancellazioni avviene all’interno del settore “singoletto” (dove gluoni e la somma di tutti i quark evolvono insieme) e che le grandi cancellazioni viste nella base di sapore sono in gran parte un artefatto della scelta di base e delle correlazioni indotte dall’evoluzione DGLAP. Affascinante, vero?

Validiamo il Passato: L’Approssimazione K-Factor è Affidabile?

Come dicevo, prima delle nostre griglie NNLO, si usava spesso l’approssimazione basata su griglie NLO più K-factor NNLO calcolati con una PDF di riferimento. Ma quanto era buona questa approssimazione? La scelta della PDF avrebbe potuto amplificare o ridurre le cancellazioni e quindi influenzare il risultato?

Abbiamo usato le nuove griglie per confrontare le previsioni NNLO esatte ottenute con diversi set di PDF. Le differenze tra i set sono a livello di qualche percento, generalmente coperte dalle rispettive incertezze PDF. Ma la cosa cruciale da guardare non è tanto la sezione d’urto totale, quanto i K-factor stessi (il rapporto tra NNLO e NLO). Sono stabili al variare della PDF?

La risposta è sì! Abbiamo scoperto che, mentre la sezione d’urto NNLO varia del qualche percento cambiando PDF, i K-factor sono incredibilmente stabili: le loro variazioni sono solo a livello di qualche per mille! Questo significa che l’impatto dell’approssimazione K-factor sulla sezione d’urto totale NNLO è stimato essere minuscolo, nell’ordine dello 0.01‰. Quindi, l’approssimazione era fondamentalmente solida.

L’Impatto sui Fit delle PDF: Tiriamo le Somme

Ma la prova del nove è vedere l’impatto nel contesto reale dei fit globali delle PDF. Un fit delle PDF è un processo complicatissimo che confronta migliaia di punti sperimentali con le previsioni teoriche. Senza la velocità delle griglie (o delle “Fast Kernel tables” che si possono derivare da esse), sarebbe praticamente impossibile.

Abbiamo quindi usato il framework di fitting open-source NNPDF per eseguire dei fit in diversi scenari: usando le nostre griglie NNLO esatte per il DY oppure usando l’approssimazione K-factor. Abbiamo provato sia usando solo dati DY (“DY only fit”, lo scenario peggiore per l’approssimazione) sia usando il dataset globale completo di NNPDF4.0.

I risultati? Anche nello scenario “DY only”, l’impatto dell’approssimazione K-factor sulle PDF risultanti è minimo, ben dentro le incertezze. Quando si usa il dataset globale (dove altri dati come il DIS sono già trattati con NNLO esatto), l’effetto dell’approssimazione sul DY diventa completamente trascurabile. Le differenze si vedono solo nelle regioni di estrapolazione, dove piccole differenze numeriche non sono compensate dai dati.

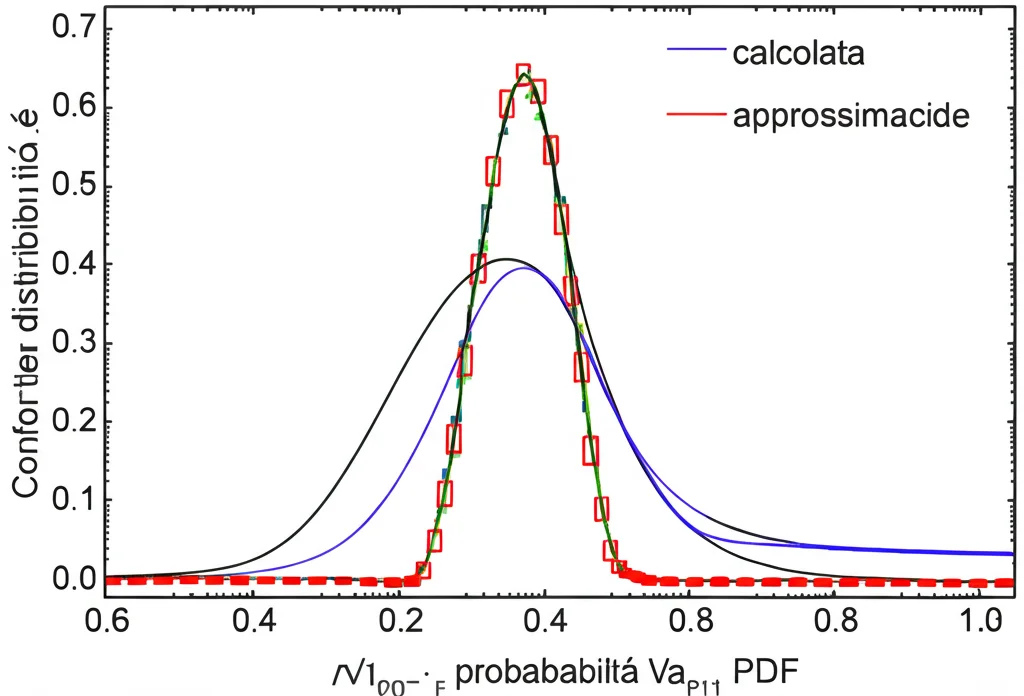
Possiamo quindi concludere con sicurezza che l’approssimazione K-factor per il Drell-Yan era valida e sicura nel contesto dei fit delle PDF. Questo risultato non era scontato, ma è una conseguenza delle osservazioni sulle cancellazioni dominate dall’evoluzione DGLAP: poiché l’evoluzione è la stessa per tutte le PDF (a un dato ordine), il pattern di cancellazioni è preservato, rendendo il K-factor stabile.

Conclusioni e Prospettive Future

In sintesi, abbiamo creato una nuova potente interfaccia tra NNLOjet e pineappl, abbiamo prodotto e rilasciato un set completo di griglie NNLO per il processo Drell-Yan, abbiamo capito meglio le cancellazioni accidentali in questo processo e abbiamo validato l’approssimazione K-factor usata finora.

Queste griglie non solo permettono analisi più precise oggi, ma aprono anche la strada all’incorporazione delle previsioni N³LO nei futuri fit delle PDF. Produrre griglie N³LO complete è ancora proibitivo (si parla di milioni di ore CPU!), ma le nostre griglie NNLO sono un ingrediente chiave per costruire approssimazioni N³LO basate su K-factor N³LO, un passo intermedio fondamentale verso la prossima frontiera della precisione nella fisica delle particelle!

Fonte: Springer