GGNN: Dimentica la Forza Bruta, l’Image Matching Diventa Intelligente (e Veloce!)

Ciao a tutti! Oggi voglio parlarvi di una sfida affascinante nel mondo della computer vision: l’image matching, ovvero come insegnare a un computer a riconoscere che due immagini diverse ritraggono la stessa scena o lo stesso oggetto. Pensate a quando create una foto panoramica con lo smartphone o a come funzionano le mappe 3D: alla base c’è sempre un processo che deve “allineare” le immagini trovando punti corrispondenti.

Per anni, l’approccio standard è stato un po’ “brutale”: prendi tutti i punti di interesse (chiamiamoli features) da un’immagine e confrontali uno per uno con tutti quelli dell’altra immagine, cercando il “vicino più prossimo” (Nearest Neighbor o NN) nello spazio dei descrittori. Funziona, sì, ma immaginate di doverlo fare con migliaia di punti per ogni coppia di immagini… diventa un lavoro enorme e lento! La complessità cresce in modo quadratico ((theta (n^2))), il che significa che raddoppiando i punti, il tempo necessario quadruplica. Un bel problema se si cerca efficienza.

Certo, sono nate alternative. Alcuni metodi provano a velocizzare cercando vicini “approssimati” (Approximate Nearest Neighbors, ANN), ma spesso sacrificano l’accuratezza. Altri, come il sofisticato AdaLAM, sono più intelligenti e filtrano le corrispondenze usando informazioni geometriche, ma lo fanno *dopo* la ricerca esaustiva iniziale, limitando i guadagni in termini di velocità.

Il Problema con l’Approccio Tradizionale

Qui ci siamo chiesti: ma siamo sicuri che serva davvero trovare il match *matematicamente* più simile per ogni singolo punto? Spesso, specialmente con pattern ripetitivi (pensate a un muro di mattoni o a una foresta), il punto più simile a livello di descrittore potrebbe essere quello geometricamente sbagliato. Questi “falsi amici” non solo sono inutili, ma rallentano anche i passaggi successivi che cercano di eliminarli usando la coerenza geometrica (come RANSAC). È come cercare l’ago nel pagliaio, ma con un sacco di spilli che sembrano aghi! L’approccio NN tradizionale è una “leaky abstraction”, un concetto che non cattura appieno la realtà geometrica del problema.

La Nostra “Eureka!”: Raggruppare per Vincere!

E se cambiassimo prospettiva? Invece di cercare ossessivamente il singolo match perfetto, perché non cercare corrispondenze *geometricamente significative* e *sufficientemente simili*, ma in modo molto più efficiente? Da qui nasce la nostra idea: Group-Guided Nearest Neighbors (GGNN).

L’intuizione chiave è gerarchica:

1. Prima raggruppiamo spazialmente le features in “zone” sull’immagine.
2. Poi, troviamo le corrispondenze tra questi *gruppi* di features tra le due immagini.
3. Infine, cerchiamo le corrispondenze delle singole features *solo all’interno* delle coppie di gruppi che abbiamo già abbinato.

Pensatela così: invece di cercare ogni singolo amico in una folla enorme (immagine B) partendo da ogni amico in un’altra folla (immagine A), prima individuiamo gruppi di amici che potrebbero essere andati insieme da A a B, e poi cerchiamo le corrispondenze individuali solo all’interno di quei gruppi ristretti. Molto più mirato, no?

Questo approccio cambia le carte in tavola a livello di complessità: passiamo da (theta (n^2)) a (theta (n sqrt{n})). Un bel salto in avanti in termini di efficienza!

Come Funziona GGNN Sotto il Cofano

Ok, l’idea è carina, ma come si realizza in pratica? Ecco i passaggi principali del nostro sistema GGNN:

• Estrazione e Descrizione delle Features: Usiamo algoritmi standard (come FAST per trovare i punti chiave) ma con un tocco in più per i descrittori. Abbiamo bisogno di vettori che rappresentino le features in modo che quelli di features diverse siano il più possibile “ortogonali” tra loro. Abbiamo scoperto che concatenare descrittori binari ad alta dimensionalità (come LATCH e BEBLID, arrivando a 1024 dimensioni!) funziona bene. Questo si ispira ai principi del calcolo iperdimensionale, dove vettori molto lunghi e quasi ortogonali possono rappresentare simboli distinti. Applichiamo anche una soppressione dei non-massimi per distanziare un po’ i punti chiave, aiutando l’ortogonalità.
• Raggruppamento Spaziale: Come creiamo i gruppi? Abbiamo provato varie strategie, ma la più semplice ed efficace è stata usare cerchi di dimensioni fisse (e sovrapposti) campionati su una griglia regolare sull’immagine. Per gestire meglio le differenze di scala tra immagini, usiamo una sorta di piramide con cerchi di dimensioni variabili. Il numero di gruppi? Circa (sqrt{n}), dove n è il numero totale di features.
• Descrizione dei Gruppi: Come descriviamo un intero gruppo con un solo vettore? Semplice: sommiamo i vettori (in rappresentazione bipolare +/-1) di tutte le features nel gruppo. Grazie all’alta dimensionalità e alla quasi-ortogonalità, questa somma (“bundling” nel gergo del calcolo iperdimensionale) funziona sorprendentemente bene come rappresentazione aggregata.
• Matching dei Gruppi: Ora confrontiamo i descrittori dei (sqrt{n}) gruppi tra le due immagini usando la similarità coseno. Facciamo un matching bidirezionale e teniamo solo i migliori (circa il 50%) per eliminare quelli di bassa qualità.
• Matching delle Features (Guidato dai Gruppi): Questo è il cuore dell’efficienza. Per ogni coppia di gruppi che abbiamo abbinato, cerchiamo le corrispondenze tra le features *contenute solo in quei due gruppi* (circa (sqrt{n}) features per gruppo). Usiamo filtri come la mutua consistenza (MNN) e verifiche geometriche locali (con RANSAC multipli in parallelo) per pulire subito i match.
• Robust Estimation e Refinement: Raccogliamo tutti i match di features trovati. Usiamo RANSAC (nella variante GC-RANSAC) per stimare la trasformazione geometrica (es. omografia) tra le immagini. Poi, usiamo questa stima iniziale per guidare un’ulteriore ricerca di corrispondenze (guided matching) in piccole aree attorno alla posizione prevista dei punti, usando il classico Ratio Test di Lowe e filtri sulla scala. Infine, ri-eseguiamo RANSAC con una soglia di errore più stretta per ottenere la trasformazione finale precisa.

Questo flusso gerarchico non solo è più veloce, ma aiuta anche a trovare match migliori perché riduce drasticamente lo spazio di ricerca per ogni feature.

Alla Prova dei Fatti: GGNN Batte la Concorrenza?

Le idee sono belle, ma funzionano nel mondo reale? Abbiamo messo alla prova GGNN su dataset classici e moderni per l’image matching e la stima di omografia (Oxford+, Homogr con variazioni sintetiche, HPatches). Abbiamo confrontato GGNN con un bel po’ di metodi:

• Metodi classici: NN, MNN, SNN (quello col Ratio Test).
• Varianti geometriche: FGINN.
• Metodi recenti e potenti: AdaLAM, SMNN.
• Strategie gerarchiche/preemptive.
• Metodi approssimati veloci: FLANN (basato su alberi), HNSW (basato su grafi, state-of-the-art per ANN).

Per un confronto equo, tutti i metodi usavano le stesse features, gli stessi descrittori (dove applicabile) e lo stesso post-processing (guided matching e GC-RANSAC).

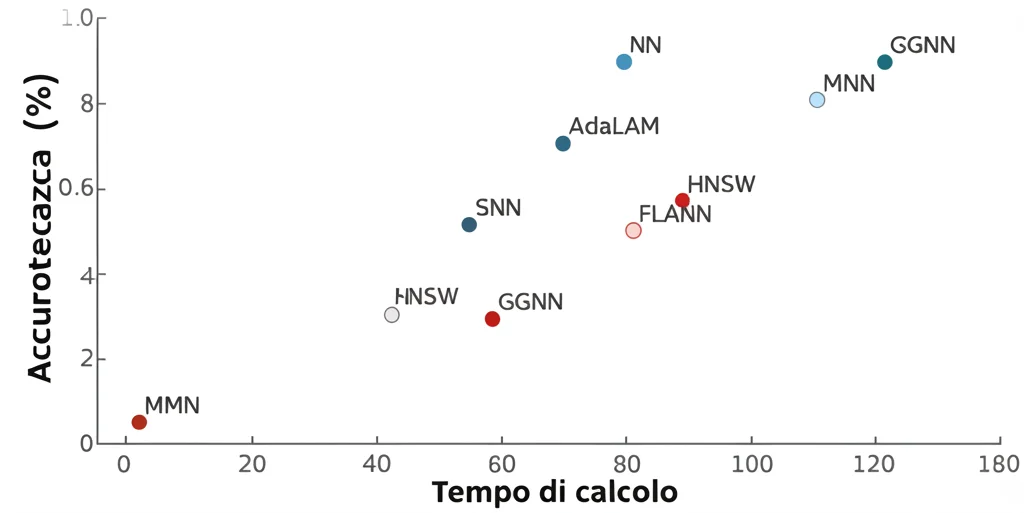
I risultati? Fantastici! GGNN si è dimostrato Pareto ottimale: per il suo livello di efficienza (e anche per livelli superiori), nessun altro metodo ha raggiunto la sua accuratezza. In pratica, GGNN ha superato sia il classico NN che il sofisticato AdaLAM su tutti i dataset, pur essendo più veloce. È interessante notare che, mentre i metodi approssimati come FLANN e HNSW sono *limitati* a raggiungere al massimo l’accuratezza di NN, il nostro GGNN può *superarla*. Perché? Se il matching dei gruppi funziona bene, trovare le corrispondenze delle features all’interno dei gruppi corretti diventa un compito più facile e meno ambiguo rispetto alla ricerca globale, portando a risultati migliori.

Più di un Semplice Trucco: Un Framework Flessibile

Abbiamo parlato di usare (g = sqrt{n}) gruppi. Ma GGNN è in realtà un framework più generale. Possiamo pensare di avere (g) gruppi, ognuno con (c = n/g) features. Il numero totale di confronti tra descrittori diventa circa (g^2 + n^2/g). Il caso del NN standard è semplicemente quando (g=1) (1 gruppo globale, (1 + n^2) confronti). Il nostro setting (g = sqrt{n}) porta a (n + nsqrt{n}) confronti. Si può dimostrare che il minimo teorico di confronti si ha con un numero di gruppi leggermente diverso ((g approx n^{2/3})).

Questo significa che possiamo scegliere il numero di gruppi (g) in base al tempo che abbiamo a disposizione! Se abbiamo pochissimo tempo, possiamo aumentare (g) (fino al minimo teorico) per ridurre i calcoli, magari accettando una piccola perdita di accuratezza. Se vogliamo la massima accuratezza possibile con questo approccio, possiamo usare (g = sqrt{n}) o un valore vicino. Questa flessibilità è un altro vantaggio.

Nessuna Bacchetta Magica: Limiti e Futuro

Ovviamente, GGNN non è perfetto. Ci sono potenziali fonti di errore:

1. Mancanza di sovrapposizione tra regioni: Se le regioni campionate non si sovrappongono abbastanza tra le immagini (es. per grandi differenze di scala), il matching fallisce. Il nostro campionamento sistematico e la piramide di regioni aiutano molto a mitigare questo.
2. Errori nel matching dei gruppi: A volte i descrittori aggregati non sono abbastanza distintivi, o ci sono strutture ripetitive che ingannano il matching dei gruppi. Questo è un limite intrinseco, ma in pratica non serve che *tutti* i gruppi siano corretti, basta un numero sufficiente di buoni match. Inoltre, filtriamo i match di gruppo di bassa qualità.
3. Errori nel matching delle features (dentro i gruppi): Anche con gruppi corretti, le singole features possono essere abbinate male. Tuttavia, il problema è molto più contenuto rispetto alla ricerca globale.

Nonostante questi limiti, i risultati sperimentali dimostrano che l’approccio funziona egregiamente.

Guardando al futuro, una limitazione attuale è che il nostro metodo non è completamente “agnostico” rispetto alle features (abbiamo ottimizzato per descrittori binari concatenati). Tuttavia, la filosofia di base dovrebbe funzionare anche con altri tipi di descrittori, specialmente se ad alta dimensionalità, dove la tendenza all’ortogonalità è naturale. Anzi, usare un singolo estrattore potente potrebbe persino migliorare i risultati riducendo le correlazioni interne ai descrittori.

In conclusione, con GGNN abbiamo dimostrato che non serve per forza la forza bruta per l’image matching. Raggruppando intelligentemente le features e adottando un approccio gerarchico, possiamo ottenere risultati più veloci *e* spesso più accurati. È un passo avanti entusiasmante per tante applicazioni che dipendono da un image matching efficiente e robusto!

Fonte: Springer