Fluidi Ribelli e Tubi Stretti: Viaggio nel Cuore del Flusso Herschel-Bulkley in Anello!
Ciao a tutti, appassionati di scienza e curiosi! Oggi voglio portarvi con me in un’avventura affascinante nel mondo dei fluidi, ma non quelli semplici e prevedibili come l’acqua. Parleremo di fluidi “non-newtoniani”, sostanze un po’ bizzarre che cambiano comportamento a seconda di come vengono sollecitate. Pensate al ketchup: fermo è denso, ma se lo agitate diventa più liquido. Ecco, questo è un esempio!
Nel mio campo, specialmente quando si ha a che fare con l’ingegneria chimica, meccanica o petrolifera, incontriamo spesso questi fluidi speciali. Uno dei modelli matematici più gettonati per descriverli è il modello di Herschel-Bulkley (HB). È considerato super accurato, quasi il “campione” dei modelli per fluidi come i fanghi di perforazione usati per estrarre petrolio e gas.
Ma cos’è questo Modello Herschel-Bulkley?
Immaginate un fluido che non inizia a scorrere finché non gli applicate una certa forza minima (chiamata “yield stress” o sforzo di soglia). Una volta superata questa soglia, il suo comportamento può ancora essere complesso, magari diventando meno viscoso (“shear-thinning”) man mano che scorre più velocemente. Il modello HB cattura proprio queste caratteristiche con tre parametri chiave. È più sofisticato dei modelli più semplici come il Bingham Plastic (BP) o il Power-Law (PL), che usano solo due parametri.
Perché è così importante? Beh, pensate alle operazioni di perforazione: il fango deve trasportare i detriti di roccia in superficie, raffreddare la punta e mantenere stabile il pozzo. Capire esattamente come scorre questo fango è cruciale per l’efficienza e la sicurezza. E spesso, questo fango si comporta proprio come un fluido HB.
Il Problema: Un “Buco” nella Letteratura
Qui arriva il punto interessante. Mentre per i modelli BP e PL esistevano già derivazioni matematiche chiare e validate, per il nostro campione, l’HB, la situazione era… nebulosa. Soprattutto quando si trattava di capire come scorre in una geometria particolare chiamata “anello”.
Cos’è un anello in questo contesto? Immaginate il tubo di perforazione che scende nel pozzo. Lo spazio tra la parete esterna del tubo di perforazione e la parete interna del pozzo è l’anello. È proprio lì che il fango risale portando con sé i detriti. E indovinate un po’? In questa zona, il flusso è spesso laminare (cioè ordinato, non turbolento), rendendo il modello HB ancora più rilevante.
Mancava, però, una spiegazione passo-passo, chiara e dettagliata, su come ricavare le equazioni che descrivono velocità, portata, velocità media e persino le stime della perdita di pressione per il flusso HB in un anello. Sembra strano, vero? Un modello così importante, ma con una derivazione matematica non completamente sviscerata e accessibile.
La Sfida: Mettere Ordine nel Caos
Ecco dove entra in gioco il mio lavoro e quello che voglio raccontarvi. Mi sono detto: “Dobbiamo colmare questa lacuna!”. È fondamentale non solo per le applicazioni pratiche, ma anche per chi verrà dopo di noi – studenti, ricercatori – che magari vorranno sviluppare modelli ancora migliori. Senza una base solida e chiara, come si fa a costruire qualcosa di nuovo?
Così, ci siamo messi all’opera per derivare, passo dopo passo, tutte le equazioni necessarie per descrivere il flusso laminare di un fluido HB in un anello. Non solo le equazioni base, ma anche quelle per la velocità media, la portata, e persino le velocità relative all’interno del flusso.
Un Diagramma di Flusso per Guidare la Derivazione
Per rendere il tutto il più chiaro possibile, abbiamo creato una sorta di “mappa”, un diagramma di flusso metodologico. Immaginatelo come una ricetta di cucina dettagliata in 7 passi:
- Bilancio delle Forze: Si parte stabilendo l’equilibrio tra le forze di taglio (dovute alla viscosità e allo sforzo di soglia) e le forze di pressione che spingono il fluido.
- Condizioni al Contorno: Si definisce cosa succede ai bordi: la velocità del fluido è zero a contatto con le pareti del tubo e del pozzo, e lo sforzo di taglio al confine della zona di “plug flow” (dove il fluido si muove come un blocco rigido) è uguale allo sforzo di soglia.
- Incremento di Velocità: Si calcola come cambia la velocità infinitesima (dV) muovendosi attraverso l’anello.
- Equazioni della Velocità: Integrando il passo precedente e applicando le condizioni al contorno, si ottengono le equazioni che descrivono la velocità del fluido in ogni punto dell’anello.
- Portata: Integrando la velocità sull’intera area dell’anello, si calcola quanta massa di fluido passa in un dato tempo (la portata, q).
- Velocità Media e Relativa: Dalla portata si ricava la velocità media. Dividendo la velocità puntuale per quella media, si ottengono le velocità relative, utili per capire il profilo del flusso.
- Soluzione Numerica per la Pressione: Infine, si sviluppa un metodo iterativo per calcolare la caduta di pressione lungo l’anello, un parametro fondamentale per la progettazione.
Seguendo questi passi, siamo riusciti a derivare in modo esplicito e dettagliato tutte le equazioni necessarie. Un lavoro meticoloso, ma fondamentale per avere una base solida.
Non Solo Teoria: La Prova dei Fatti (e Qualche Sorpresa)
Ma la matematica da sola non basta. Come sapere se le nostre belle equazioni funzionano nel mondo reale? Abbiamo preso dei dati sperimentali pubblicati da altri ricercatori (Okafor ed Evers, 1992) che avevano misurato le perdite di pressione reali di un fluido HB in un anello.
Abbiamo confrontato le previsioni del nostro modello numerico (derivato seguendo i 7 passi) e di altri due metodi di stima della pressione (quello di Merlo et al. e quello di Gjerstad e Time, di cui abbiamo anche chiarito la derivazione matematica) con queste misure sperimentali.
E qui arriva la sorpresa. Il modello HB, considerato il “gold standard”, ha mostrato un errore percentuale assoluto medio di circa il 32% rispetto ai dati sperimentali! Non proprio l’accuratezza infallibile che ci si aspettava. Certo, è meglio di altri modelli più semplici in molte situazioni, ma un errore del 32% non è trascurabile.
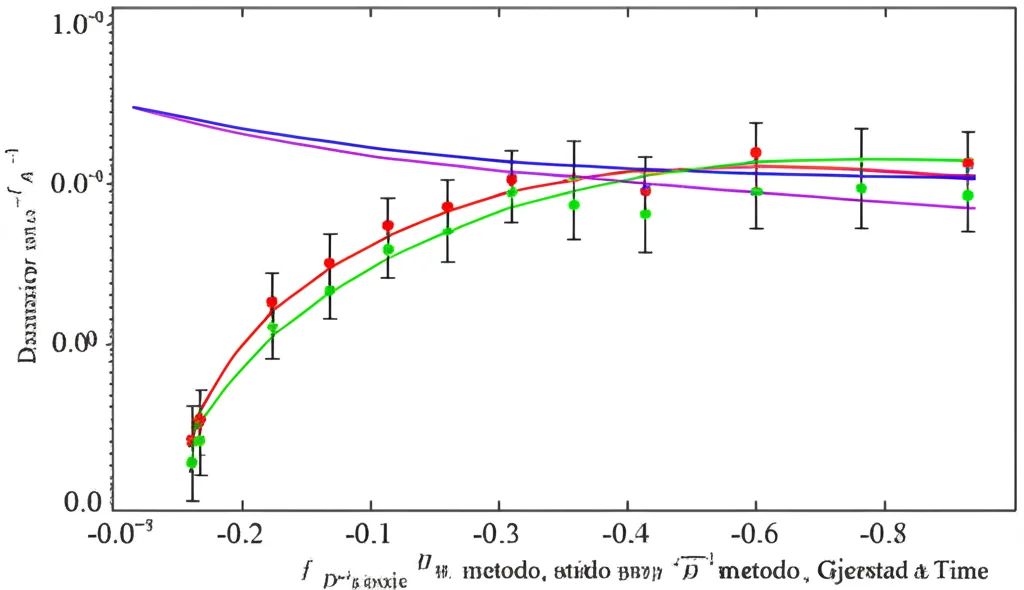
Il metodo di Gjerstad e Time sembrava dare risultati leggermente migliori (errore medio del 28%), ma è stato sviluppato proprio per approssimare la soluzione numerica, quindi non è detto sia intrinsecamente più “corretto”. Il punto chiave è che il modello HB “puro”, derivato dalla teoria, non è così perfetto come si pensava.
Cosa Significa Tutto Questo?
Questo risultato non sminuisce l’importanza del modello HB, che rimane uno strumento utilissimo. Tuttavia, evidenzia la necessità di continuare la ricerca. C’è spazio per sviluppare modelli reologici nuovi e più precisi, capaci di descrivere ancora meglio il comportamento di questi fluidi complessi, specialmente in condizioni operative reali.
Il nostro lavoro, quindi, non è solo una “pulizia” matematica di un modello esistente. È soprattutto un contributo fondamentale:
- Fornisce una metodologia chiara e dettagliata (il diagramma di flusso!) che può essere usata come guida per derivare e validare futuri modelli di fluidi non-newtoniani.
- Mette a disposizione le derivazioni matematiche complete per l’HB in anello e per i metodi di stima della pressione, rendendole accessibili a studenti e ricercatori.
- Solleva un punto critico sull’accuratezza del modello HB, stimolando ulteriori ricerche per modelli più performanti.
In pratica, abbiamo costruito delle fondamenta più solide e abbiamo indicato dove potrebbero esserci delle crepe, aprendo la strada a future costruzioni più avanzate nel campo affascinante dei fluidi non-newtoniani. E chissà quali scoperte ci riserva il futuro!
Fonte: Springer