Equazioni di Lyapunov: La Chiave Deterministica per Svelare le SPDE Stocastiche

Ciao a tutti! Oggi voglio portarvi in un viaggio affascinante nel mondo della matematica applicata, un posto dove cerchiamo di dare un senso a sistemi complessi che evolvono nel tempo e nello spazio, ma con un pizzico (o a volte una valanga!) di casualità. Parliamo delle Equazioni Differenziali alle Derivate Parziali Stocastiche, o SPDE per gli amici. Immaginate di studiare come il calore si diffonde in un materiale, ma tenendo conto di fluttuazioni casuali della temperatura, o come si muovono le particelle in un fluido turbolento. Ecco, le SPDE ci aiutano a modellare proprio questo tipo di fenomeni.

Ma modellare non basta, spesso vogliamo capire proprietà specifiche di questi sistemi, come la loro stabilità a lungo termine o il valore medio di certe quantità. Ed è qui che entrano in gioco le nostre protagoniste di oggi: le Equazioni di Lyapunov.

Cosa c’entrano le Equazioni di Lyapunov?

Forse avete già sentito parlare delle equazioni di Lyapunov nel contesto dei sistemi dinamici deterministici, dove sono uno strumento potentissimo per analizzare la stabilità. Bene, si scopre che hanno un ruolo cruciale anche nel mondo stocastico! In particolare, per le SPDE lineari con un certo tipo di “rumore” (il termine tecnico è rumore moltiplicativo), la soluzione di un’equazione di Lyapunov operatore-valutata ci dà informazioni preziose.

Nello specifico, e questa è una delle cose che mi affascina di più, la soluzione dell’equazione di Lyapunov è direttamente collegata a un tipo particolare di “funzionale quadratico” della soluzione della SPDE. In parole povere, ci permette di calcolare il valore atteso di una quantità che dipende dall’intera traiettoria (il “percorso”) della soluzione della SPDE, e lo fa in modo deterministico! Pensateci: invece di dover simulare tantissime possibili evoluzioni casuali del sistema (come faremmo con un metodo Monte Carlo), possiamo risolvere *una sola* equazione deterministica (l’equazione di Lyapunov) per ottenere la stessa informazione. Forte, no?

Il lavoro di cui vi parlo oggi si concentra proprio su questo legame e su come possiamo approssimare numericamente queste equazioni di Lyapunov. Perché, vedete, queste equazioni vivono spesso in spazi a dimensione infinita (spazi di Hilbert, per i più tecnici), e per metterle sul computer dobbiamo per forza discretizzarle.

La Sfida dell’Approssimazione: Elementi Finiti e Passi Temporali

Come facciamo a portare queste equazioni dal mondo astratto degli spazi infiniti al mondo concreto dei computer? Usiamo due tecniche principali:

• Metodo degli Elementi Finiti (FEM): Per discretizzare lo spazio, suddividiamo il dominio fisico (ad esempio, la barra di metallo in cui si diffonde il calore) in tanti piccoli pezzetti (triangoli, tetraedri…) e approssimiamo la soluzione su questi elementi. È una tecnica super versatile e potente, usatissima in ingegneria e fisica.
• Schema di Eulero Semi-Implicito: Per discretizzare il tempo, avanziamo passo dopo passo, usando uno schema numerico. Quello che abbiamo usato noi è una variante dello schema di Eulero, chiamato “semi-implicito”, che ha buone proprietà di stabilità per questo tipo di problemi.

Quindi, prendiamo la nostra bella equazione di Lyapunov e la trasformiamo in un sistema di equazioni (grosso, ma finito!) che il computer può risolvere. Lo stesso facciamo per la SPDE originale.

Il Cuore della Ricerca: Analisi di Convergenza e Tassi Ottimali

Ok, abbiamo le nostre approssimazioni. Ma quanto sono buone? Si avvicinano alla soluzione vera man mano che raffiniamo la nostra discretizzazione (cioè, usiamo elementi più piccoli e passi temporali più corti)? E quanto velocemente? Questa è l’analisi di convergenza, ed è il nocciolo del nostro lavoro.

Quello che siamo riusciti a dimostrare è piuttosto interessante:

1. Convergenza dell’Approssimazione di Lyapunov: Abbiamo derivato il tasso di convergenza per l’approssimazione completamente discreta (spazio e tempo) dell’equazione di Lyapunov. Misuriamo l’errore in una norma specifica (la norma operatore) e otteniamo stime precise di quanto velocemente l’errore diminuisce al raffinare della discretizzazione.
2. Il Legame Resiste all’Approssimazione: Abbiamo mostrato che la bellissima connessione tra l’equazione di Lyapunov e il funzionale quadratico della SPDE vale anche per le loro versioni discretizzate, a meno di un piccolo errore che svanisce rapidamente.
3. Convergenza Debole Raddoppiata per la SPDE: Questo è forse il risultato secondario più succoso. Grazie al punto precedente, siamo riusciti a stabilire tassi di convergenza debole per l’approssimazione della SPDE. La cosa notevole è che questo tasso è il doppio del tasso di convergenza forte! Questo tipo di risultato era noto per altri metodi o casi più semplici, ma per l’approssimazione agli elementi finiti completamente discreta di SPDE con rumore moltiplicativo (anche “smooth” nello spazio) e per funzionali che dipendono dall’intera traiettoria, è una novità importante. È la prima volta che si ottiene questo raddoppio del tasso in questo contesto specifico.

Perché è importante questo raddoppio? Perché ci dice che per calcolare quantità medie (come il nostro funzionale quadratico), il nostro metodo numerico converge molto più velocemente di quanto ci si aspetterebbe guardando solo l’errore su una singola traiettoria.

Metodo Deterministico vs. Monte Carlo: Quando Lyapunov Vince

Come accennavo prima, abbiamo due strade principali per calcolare il nostro funzionale quadratico (Phi(x)):

• Metodo Monte Carlo: Simuliamo la SPDE discretizzata (X_{h,tau}) un gran numero di volte (M volte), partendo sempre da (x), e poi facciamo la media dei risultati. Concettualmente semplice, facile da parallelizzare.
• Metodo di Lyapunov (Deterministico): Risolviamo l’equazione di Lyapunov discretizzata (L^n_{h,tau}) una sola volta per ottenere l’operatore (L^{N_tau}_{h,tau}) e poi calcoliamo (langle L^{N_tau}_{h,tau} P_h x, P_h x rangle).

Quando conviene usare il nostro metodo deterministico basato su Lyapunov? Abbiamo identificato alcune situazioni chiave:

1. Calcolo per Molte Condizioni Iniziali: Se dobbiamo calcolare (Phi(x)) per tanti valori diversi di (x), il metodo di Lyapunov è imbattibile. Risolviamo l’equazione una volta e otteniamo l’operatore (L^{N_tau}_{h,tau}) che funziona per *tutti* gli (x). Con Monte Carlo, dovremmo rifare tutte le simulazioni per ogni nuovo (x).
2. Operatori Non Locali: Se l’operatore R nel funzionale è “non locale” (cioè agisce su tutto il dominio contemporaneamente), la sua rappresentazione matriciale ({textbf{R}}_h) è densa. Nel Monte Carlo, dovremmo moltiplicare per questa matrice densa ad ogni passo temporale e per ogni simulazione, un costo computazionale enorme. Nel metodo di Lyapunov, operazioni simili con matrici dense avvengono, ma solo una volta per passo temporale.
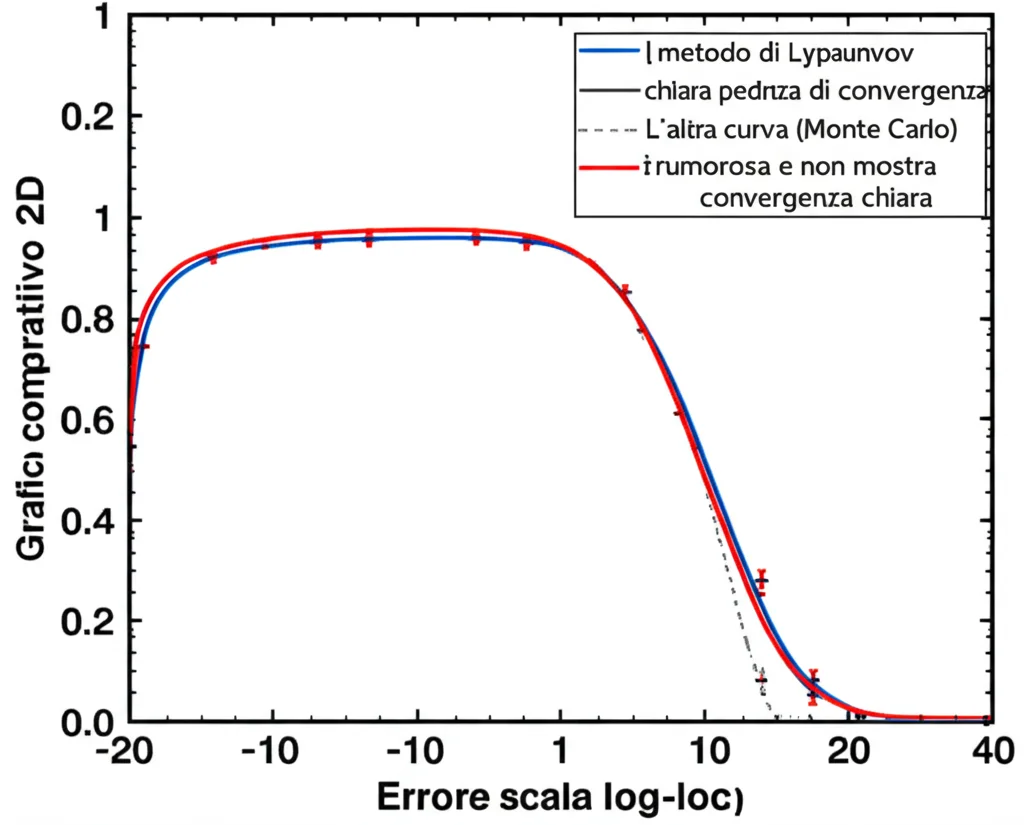
3. Problemi di Stabilità: Questo è un punto cruciale e affascinante. Può succedere che la soluzione nulla (X=0) della SPDE sia stabile “quasi sicuramente” (cioè, quasi tutte le traiettorie vanno a zero) ma instabile “in media quadratica” (cioè, il valore atteso di (Vert X(t) Vert^2) cresce o non va a zero). Questo succede tipicamente quando il rumore moltiplicativo è forte. In questi casi, il metodo Monte Carlo fallisce miseramente! Poche traiettorie “esplodono” e dominano la media, rendendo necessaria una quantità proibitiva di simulazioni per ottenere una stima decente. Il nostro metodo deterministico, invece, non soffre di questo problema e fornisce risultati affidabili. Abbiamo mostrato questo comportamento con esperimenti numerici: per valori crescenti del rumore e tempi più lunghi, il Monte Carlo dava risultati completamente sballati, mentre il metodo di Lyapunov rimaneva accurato.

Uno Sguardo alla Matematica (Senza Paura!)

Dietro tutto questo c’è una solida impalcatura matematica. Lavoriamo in spazi di Hilbert separabili (H) e (U). L’operatore (A) nella SPDE è autoaggiunto, positivo definito, con inversa compatta (come il Laplaciano, per esempio) e genera un semigruppo analitico (S(t)), che descrive l’evoluzione deterministica del sistema. Il rumore è modellato da un processo di Wiener cilindrico (W), che è un concetto molto generale di rumore bianco in spazi infinito-dimensionali. L’operatore (B) modella come il rumore interagisce con lo stato del sistema (il termine moltiplicativo).

Abbiamo dovuto prima di tutto sviluppare la teoria della soluzione per l’equazione di Lyapunov nel nostro contesto generale (con rumore cilindrico), dimostrando esistenza, unicità e regolarità della soluzione (L(t)). Sorprendentemente, anche se le equazioni di Lyapunov sono studiate da tempo, il nostro setting specifico non era completamente coperto dalla letteratura esistente. Abbiamo usato tecniche standard come il teorema del punto fisso di Banach e il lemma di Gronwall, ma adattate al nostro caso.

L’analisi di convergenza poi si basa su stime accurate dell’errore introdotto dalla discretizzazione spaziale (usando le proprietà degli spazi di elementi finiti (V_h)) e temporale (usando le proprietà dello schema di Eulero implicito (S_{h,tau})). Richiede un bel po’ di lavoro tecnico con norme di operatori, potenze frazionarie di (A), e stime di regolarità del semigruppo e delle soluzioni.

Conclusioni e Prospettive

In sintesi, abbiamo fatto un’analisi numerica completa per l’approssimazione di equazioni di Lyapunov legate a SPDE paraboliche con rumore moltiplicativo. Abbiamo stabilito tassi di convergenza rigorosi per schemi completamente discreti (elementi finiti + Eulero semi-implicito) e, cosa fondamentale, abbiamo usato questo risultato per dimostrare tassi di convergenza debole ottimali (il doppio di quelli forti) per l’approssimazione della SPDE stessa, anche per funzionali dipendenti dal percorso e rumore spazialmente regolare.

Abbiamo anche evidenziato i vantaggi pratici del metodo deterministico basato su Lyapunov rispetto al classico Monte Carlo, specialmente in termini di efficienza per certi problemi e, soprattutto, di robustezza in presenza di instabilità media quadratica.

Questo lavoro apre la strada a future ricerche, ad esempio estendendo questi risultati alle equazioni di Riccati, che sono la versione non lineare delle equazioni di Lyapunov e compaiono nei problemi di controllo ottimo stocastico e di filtraggio. È un campo di ricerca davvero stimolante! Spero di avervi trasmesso un po’ della mia passione per questi argomenti. Alla prossima!

Fonte: Springer