Legno Lamellare e Umidità: Sveliamo i Segreti degli Anelli di Crescita per Costruzioni Più Forti!

Ciao a tutti! Oggi voglio portarvi con me in un viaggio affascinante nel mondo del legno, ma non uno qualsiasi: parleremo del legno lamellare incollato (glulam) e del suo rapporto, a volte un po’ burrascoso, con l’umidità. Sapete, il legno è un materiale fantastico per costruire: è robusto, leggero rispetto alla sua resistenza, rinnovabile e fa bene all’ambiente. Però, come ogni materiale naturale, ha i suoi “difettucci” e limiti di dimensione. Ecco perché nascono prodotti ingegnerizzati come il glulam, che ci permettono di superare questi ostacoli.

Tuttavia, c’è un nemico sempre in agguato per le strutture in legno: l’umidità. Pensate che uno studio su 245 strutture in legno di grandi dimensioni ha rivelato che le variazioni di contenuto di umidità sono responsabili del 46% dei danni strutturali! Mica poco, eh? È un problema serio che, come ricercatori, cerchiamo di affrontare con tutti gli strumenti a nostra disposizione, e uno dei più potenti è il metodo degli elementi finiti, che ci permette di simulare come il legno reagisce a diverse condizioni ambientali.

La Danza dell’Acqua nel Legno: Un Problema Complesso

Quando l’umidità nell’aria cambia, il legno “respira”: assorbe o rilascia acqua. Questo processo, chiamato idro-espansione (o ritiro, se perde acqua), è anisotropo, cioè diverso nelle varie direzioni del legno. Immaginatevi le tensioni che si creano! Questo può causare instabilità di forma durante l’essiccazione tecnica e generare stress da ritiro sia durante la produzione che per tutta la vita utile della struttura. Non solo, l’umidità influisce anche sul creep meccano-sorptivo (una deformazione lenta sotto carico e variazione di umidità) e altera parametri come la rigidezza.

Negli anni, abbiamo sviluppato modelli sempre più sofisticati per capire questi fenomeni, considerando la diffusione dell’umidità, l’idro-espansione, l’elasticità, la viscoelasticità, la meccano-sorptzione e persino il danneggiamento e la rottura per diverse specie legnose. Ma c’è un aspetto che è rimasto un po’ in ombra: l’effetto della disposizione degli anelli di crescita nel glulam.

La Sfida: Un Puzzle Infinito di Anelli e Incollaggi

Il glulam è fatto incollando insieme diverse tavole (lamelle). Ogni tavola ha una sua storia, scritta negli anelli di crescita, che dipendono dalla posizione del midollo (il centro dell’albero da cui è stata tagliata). Immaginate di dover considerare tutte le possibili combinazioni di queste lamelle, con i loro midolli orientati in modi diversi! È un numero di possibilità praticamente infinito, e studiarle tutte con simulazioni dettagliate sarebbe un’impresa titanica in termini di costi computazionali.

Alcuni studi hanno esaminato casi specifici, confermando che la disposizione della sezione trasversale influenza moltissimo la distribuzione delle tensioni. Ma come generalizzare questi risultati? Come capire quali sono i fattori davvero cruciali?

La Nostra Arma Segreta: Le Simulazioni Monte Carlo

Per affrontare questa complessità, abbiamo deciso di usare le simulazioni Monte Carlo. In pratica, abbiamo eseguito un gran numero di simulazioni variando casualmente la posizione del midollo nelle diverse lamelle. Questo ci ha permesso di capire, statisticamente, quali fattori avessero l’impatto maggiore sulle tensioni indotte dall’umidità. Abbiamo analizzato quattro diverse specie legnose, un bel po’ di parametri e una notevole variabilità. Per farlo, abbiamo scelto un modello costitutivo del materiale che fosse affidabile nel catturare il trasferimento di umidità e il comportamento elasto-fragile del legno, e per il quale fossero disponibili i parametri in letteratura.

Abbiamo costruito modelli numerici di travi in glulam con un numero variabile di strati (da 5 a 19), ognuno di 40 mm x 200 mm. Per ogni tavola, abbiamo definito un sistema di coordinate cilindriche basato sulla posizione del midollo. Poi, abbiamo simulato cosa succede quando queste travi vengono esposte a condizioni di essiccazione, partendo da un contenuto di umidità iniziale (corrispondente a 20°C e 65% di umidità relativa) e riducendolo. Abbiamo usato dati climatici reali di Monaco di Baviera per un anno intero per vedere come fluttua l’umidità di equilibrio del legno, che può variare parecchio, tra il 4% e il 28%!

Le Scoperte Chiave: Cosa Abbiamo Imparato?

E qui le cose si fanno interessanti! Analizzando i risultati delle simulazioni Monte Carlo, sono emerse due osservazioni fondamentali riguardo alle tensioni nello strato centrale (quello che ci interessava di più analizzare):

• Osservazione I: Le tensioni nello strato analizzato sono minimamente influenzate dalla disposizione degli anelli di crescita degli strati vicini. Sembra quasi che ogni lamella “pensi per sé” quando si tratta di stress da umidità, almeno per quanto riguarda l’influenza diretta dei suoi vicini.
• Osservazione II: Le tensioni mostrano una forte correlazione con l’angolo di rotazione del materiale (cioè, come sono orientati gli anelli di crescita rispetto alle facce della tavola) nella regione superficiale.

Queste scoperte sono state una vera manna dal cielo! Ci hanno aperto la strada a due livelli di semplificazione per analizzare lo stress indotto dall’umidità in modo molto più efficiente.

Primo Livello di Semplificazione: Dal Multi-Strato al Singolo Asse

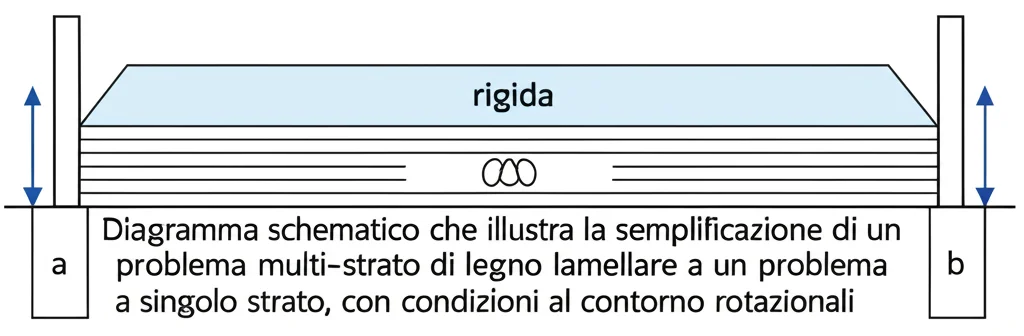
Basandoci sull’Osservazione I (l’influenza limitata degli strati adiacenti), abbiamo pensato: perché non semplificare il problema da multi-strato a uno strato singolo? In pratica, abbiamo modellato una singola tavola, e l’influenza degli strati vicini è stata “astrattizzata” in una condizione al contorno rotazionale.

Ma perché l’influenza dei vicini è così piccola? Beh, il processo di diffusione dell’umidità nel legno è lento. Dopo un mese, solo una profondità limitata della tavola è realmente influenzata dal cambiamento di umidità. La maggior parte della regione centrale rimane quasi a umidità costante e con stress zero, comportandosi come un corpo rigido. È la regione superficiale che si restringe e subisce alte tensioni. Questa restrizione è data sia dalla parte centrale della tavola stessa sia dagli strati vicini. Tuttavia, poiché la regione superficiale interessata è sottile, l’influenza della “rigidità” della parte centrale della tavola stessa domina rispetto a quella, pur presente, degli strati vicini.

Questo primo livello di semplificazione riduce drasticamente i costi di simulazione e ci permette di fare analisi più complesse sul danneggiamento, rivelando come i diversi tipi di tavole (a seconda della posizione del midollo) si danneggiano in modo differente. Ovviamente, questa semplificazione non vale per gli strati più esterni (superiore e inferiore) della trave in glulam.

Secondo Livello di Semplificazione: L’Equazione Magica

Anche se la prima semplificazione è utilissima, alcune domande rimanevano aperte: perché lo stress nella regione superficiale ha quella forte correlazione non lineare con l’angolo di rotazione? Perché questa correlazione cambia tra specie legnose diverse? Qual è il parametro materiale principale che determina lo stress massimo?

Se fossimo riusciti a derivare un’equazione analitica per spiegare questa correlazione, avremmo potuto stimare lo stress massimo per diverse specie in pochi secondi, senza simulazioni estese! Per farlo, abbiamo dovuto semplificare ulteriormente il problema, riducendolo a un singolo elemento. Abbiamo immaginato che l’influenza della regione centrale (quella che si comporta da corpo rigido) potesse essere rappresentata da una condizione al contorno fissa su un lato dell’elemento superficiale.

Trascurando gli effetti longitudinali e facendo un po’ di matematica (che vi risparmio qui, ma fidatevi, è elegante!), siamo riusciti a derivare delle equazioni che legano lo stress locale (tangenziale e radiale) all’angolo di rotazione, ai coefficienti di idro-espansione, e ai moduli elastici del legno. Voilà! Avevamo una formula per predire lo stress.

Questa seconda semplificazione è valida nel range elastico e per periodi in cui le variazioni di umidità nella regione centrale sono minime. Il suo grande vantaggio? Ci spiega chiaramente come lo stress sia influenzato dall’angolo di rotazione, dalla rigidezza e dai coefficienti di idro-espansione. Questo significa che per ogni nuova specie legnosa, possiamo avere una stima rapida del livello di stress indotto dall’umidità senza fare simulazioni numeriche. E ci fornisce informazioni come l’angolo di rotazione critico, il range critico di umidità e il tipo di tavola preferibile.

Dalla Teoria alla Pratica: Costruire Meglio e Più Durevolmente

Cosa ci dicono queste equazioni? Per esempio, possiamo calcolare lo stress per due angoli estremi: 0° e 90°. Questi corrispondono approssimativamente allo stress tangenziale massimo e allo stress radiale massimo. La tavola con il midollo al centro della sua superficie inferiore (angolo 0° sulla superficie) è spesso considerata il caso critico. Le nostre equazioni ci dicono che questo è vero se il rapporto tra modulo elastico tangenziale, coefficiente di idro-espansione tangenziale e resistenza tangenziale è maggiore del corrispettivo radiale ((frac{E_T alpha _T}{f_T}> frac{E_R alpha _R}{f_R})).

Ancora più importante, possiamo calcolare il range critico di fluttuazione dell’umidità ((Delta u_{text {critic}})). Questo è il cambiamento di contenuto di umidità che porterebbe a superare i criteri di danneggiamento. Se la variazione di umidità rimane sotto questa soglia, le tavole dovrebbero essere al sicuro da crepe da ritiro. Per esempio, per il faggio, il pino e il larice, abbiamo calcolato (Delta u_{text {critic}}) rispettivamente del 2.5%, 2.4% e 0.8%. Per l’abete rosso, usando un criterio di rottura diverso (Tsai-Wu multi-superficie), il valore è 1.4%.

Questo ci dice che il glulam fatto di faggio e pino è meno prono al danneggiamento da ritiro causato da variazioni di umidità, mentre abete rosso e larice sono più suscettibili e richiedono un controllo più stretto delle fluttuazioni di umidità.

Interessante, vero? Ma c’è di più! Possiamo vedere come questo (Delta u_{text {critic}}) cambi con l’angolo di rotazione. Per il faggio, selezionando tavole con angoli di rotazione tra 30° e 150°, il contenuto critico di umidità può aumentare al 3.1%. E se restringiamo il campo a 45°-135°, arriva addirittura al 4.7%! Similmente per l’abete rosso. Questo significa che una scelta oculata delle tavole in base all’orientamento degli anelli può davvero fare la differenza.

Come si Propaga il Danno? Uno Sguardo da Vicino

Grazie alla prima semplificazione (quella a singola tavola), possiamo studiare l’evoluzione del danno in modo più dettagliato. Abbiamo simulato 25 tipi di tavole di faggio con diverse posizioni del midollo, esposte a una variazione di umidità del 3%. Oltre al danno superficiale, abbiamo visto che un danno significativo può evolvere all’interno della tavola. Poiché il danno principale per il faggio è quello tangenziale, questo avanza principalmente in direzione radiale.

I pattern di danneggiamento simulati assomigliano qualitativamente alle crepe da essiccazione osservate in travi reali. È affascinante vedere come l’inizio del danno corrisponda ai cambiamenti di contenuto di umidità, partendo dalla superficie. Poi, a causa del danno, le aree colpite possono sopportare meno stress, portando a una ridistribuzione dello stress all’interno dell’intera tavola. Data la bassa resistenza tangenziale, si forma un danno tangenziale significativo che si propaga in direzione radiale.

Il pattern di danno varia moltissimo a seconda della posizione del midollo.

• Se il midollo è vicino alla superficie laterale della tavola, il danno rimane localizzato in superficie.
• Ma se il midollo si trova all’interno dello spessore della tavola (cioè, la sua coordinata y è piccola), il danno progredisce quasi orizzontalmente, penetrando per l’intera larghezza della tavola! E questo, capite bene, può sollevare serie preoccupazioni per la stabilità dell’intera struttura in glulam.

Un Occhio al Futuro e Qualche Cautela

È importante sottolineare che queste conclusioni si basano su simulazioni dove l’elasticità del legno è considerata indipendente dall’umidità (entro certi limiti) e non abbiamo considerato deviazioni della fibra nella direzione longitudinale. Nella realtà, specie come il faggio presentano spesso una forte curvatura della fibra, rendendo più complesso controllare gli angoli di taglio. Per queste specie, la prima semplificazione, magari implementando informazioni sulla deviazione della fibra ottenute da tecniche di scansione, potrebbe essere la via da seguire.

Tirando le Somme: Un Passo Avanti per il Legno Strutturale

Cosa portiamo a casa da tutto questo lavoro?

1. Lo stress indotto dall’umidità varia significativamente a seconda della posizione del midollo: l’effetto degli anelli di crescita è cruciale.
2. L’influenza degli strati vicini sullo stress da ritiro è minima, il che ci permette di concentrarci sulle caratteristiche della singola tavola.
3. Esiste una forte correlazione non lineare tra stress indotto dall’umidità e angolo di rotazione del materiale in superficie.

Le nostre due metodologie di semplificazione ci hanno permesso di:

• Approssimare con equazioni matematiche la relazione non lineare tra stress e parametri del materiale.
• Confermare (con condizioni precise) l’assunto comune che la tavola con il midollo al centro della superficie inferiore sia il caso più critico.
• Identificare che abete rosso e larice sono più sensibili alle fluttuazioni di umidità rispetto a faggio e pino (basandoci sui parametri di letteratura).
• Osservare che nel faggio, il danno da umidità avanza principalmente in direzione radiale e può penetrare l’intera larghezza della tavola se il midollo è posizionato “male”.

Spero che questo piccolo viaggio nel cuore del legno lamellare vi sia piaciuto! Capire questi meccanismi è fondamentale per progettare e produrre strutture in legno sempre più performanti e durevoli, capaci di resistere meglio alle insidie dell’umidità. E questo, per chi ama il legno come me, è un obiettivo entusiasmante!

Fonte: Springer