Punti che Coprono Altri Punti: Un Ballo Casuale tra Geometria e Probabilità!

Ciao a tutti, appassionati di scienza e curiosità! Oggi voglio portarvi con me in un viaggio affascinante nel mondo dei punti casuali. Sembra semplice, no? Lanciamo dei punti a caso su una superficie. Ma cosa succede se abbiamo *due* tipi di punti, diciamo blu e rossi, e vogliamo che i blu “coprano” i rossi? È qui che le cose si fanno interessanti e la matematica tira fuori delle sorprese niente male.

Immaginate di avere un’area definita, come un foglio di carta, un campo, o anche uno spazio più astratto. Ora, spargiamo a caso un certo numero, chiamiamolo *n*, di punti blu (i nostri “copritori”). Poi, nello stesso spazio (o in una sua sottozona), spargiamo un altro numero, *m*, di punti rossi (quelli da “coprire”). La domanda che ci poniamo è: qual è il raggio *minimo*, chiamiamolo *r*, che devono avere dei dischi (o sfere, se siamo in 3D) centrati sui punti blu, affinché *tutti* i punti rossi siano coperti? E se volessimo che ogni punto rosso fosse coperto non una, ma *almeno k* volte? Ecco, questa è la sfida!

La Scena del Crimine: Definire il Problema

Entriamo un po’ più nel tecnico, ma senza spaventarci. Abbiamo:

• Un dominio (A), che è la nostra area di gioco (immaginiamo un quadrato, un disco, o una forma più complessa ma “liscia” o poligonale).
• (n) punti (X_1, X_2, ldots, X_n) distribuiti uniformemente a caso in (A). Questi sono i centri dei nostri dischi coprenti.
• (m) punti (Y_1, Y_2, ldots, Y_m) distribuiti uniformemente a caso in (A) (o in una sua sottozona (B)). Questi sono i punti che devono essere coperti. Spesso consideriamo il caso in cui (m) cresce in modo proporzionale a (n), tipo (m approx tau n) per una costante (tau).
• Un numero intero (k ge 1). È il numero minimo di dischi blu che devono coprire *ogni* singolo punto rosso.

Quello che cerchiamo è la soglia di k-copertura a due campioni, che chiamiamo (R_{n,m,k}). È il più piccolo raggio *r* tale che ogni punto (Y_j) sia contenuto in almeno *k* dischi di raggio *r* centrati sugli (X_i).
Poiché la posizione dei punti è casuale, anche questo raggio (R_{n,m,k}) è una variabile casuale. La vera domanda diventa: come si comporta questa variabile quando *n* (e quindi *m*) diventa molto, molto grande? Qual è la sua distribuzione di probabilità?

Perché Ci Interessa Questa Danza di Punti?

Potrebbe sembrare un gioco matematico astratto, ma le motivazioni sono concrete. Pensate alle reti wireless: i punti blu potrebbero essere trasmettitori (antenne) e i punti rossi dei ricevitori (i nostri smartphone). Vogliamo sapere qual è la potenza (e quindi il raggio di copertura) minima necessaria affinché tutti gli utenti siano serviti. Oppure, in ecologia, i punti blu potrebbero essere semi dispersi da una pianta madre e i punti rossi delle aree target favorevoli alla crescita.
In altri scenari, come nel machine learning, capire come un set di punti ne “copre” un altro può essere legato a problemi di clustering o classificazione. Insomma, non stiamo solo giocando con i puntini!

Il Comportamento al Limite: Entra in Scena Gumbel

Quando il numero di punti *n* diventa enorme, la magia della probabilità ci dice che il comportamento della nostra soglia (R_{n,m,k}) (opportunamente riscalata e centrata) tende a stabilizzarsi verso una forma ben precisa. Spesso, questa forma è descritta dalla famosa distribuzione di Gumbel, una celebrità nel campo dei valori estremi.
In pratica, se prendiamo (n pi R_{n,m,k}^2) (che è proporzionale all’area totale dei dischi necessari, normalizzata per *n*) e gli sottraiamo qualcosa che cresce come (log n), otteniamo una variabile che assomiglia sempre di più a una Gumbel.
La cosa affascinante è che i parametri esatti di questa Gumbel (la sua “posizione” e la sua “scala” o larghezza) dipendono da *k* (quante volte dobbiamo coprire) e da (tau) (il rapporto tra punti rossi e blu).

La Sorpresa: L’Effetto Bordo!

Qui arriva il bello. Ci si potrebbe aspettare che i punti più “difficili” da coprire siano quelli nel mezzo dell’area, magari in zone rimaste scoperte per caso. E a volte è così, specialmente se ci basta coprire ogni punto rosso una sola volta (*k=1*) e siamo in 2D. In questo caso, il limite è una Gumbel “semplice” (scala 1) e il bordo dell’area (A) non sembra giocare un ruolo fondamentale nel comportamento asintotico.
Ma… se aumentiamo la richiesta, chiedendo che ogni punto sia coperto *almeno k=2* o più volte, o se passiamo a dimensioni superiori (3D o più), il bordo dell’area (A) diventa protagonista! I punti rossi più difficili da coprire *k* volte tendono ad essere quelli vicini al confine. Perché? Intuitivamente, un punto vicino al bordo ha “meno spazio intorno” da cui possono arrivare i punti blu coprenti. Ha meno “vicini” potenziali da un lato.
Questo “effetto bordo” cambia le carte in tavola:

• Per (d=2, k ge 3): Il bordo domina. La distribuzione limite è ancora Gumbel, ma con una scala diversa (scala 2) e un centraggio che dipende anche dal perimetro di (A) e coinvolge termini come (log(log n)).
• Per (d ge 3): Il bordo domina *sempre*, per qualsiasi *k*. La situazione è simile al caso precedente (Gumbel scala 2).
• Il caso (d=2, k=2) è speciale: qui l’interno e il bordo sono entrambi importanti! Il punto più difficile da coprire due volte ha una probabilità non trascurabile sia di essere all’interno che vicino al bordo. La distribuzione limite non è una semplice Gumbel, ma una combinazione di due Gumbel (una TCEV – Two-Component Extreme Value distribution). Affascinante, vero?

La Prova del Nove: Le Simulazioni al Computer

Ok, la teoria è elegante, ma funziona nel mondo “reale” (o almeno in quello simulato)? Abbiamo fatto girare i computer, generando migliaia di volte queste configurazioni di punti casuali e calcolando il raggio (R_{n,m,k}) necessario. Poi abbiamo confrontato la distribuzione ottenuta dalle simulazioni con le previsioni teoriche (le Gumbel o TCEV).
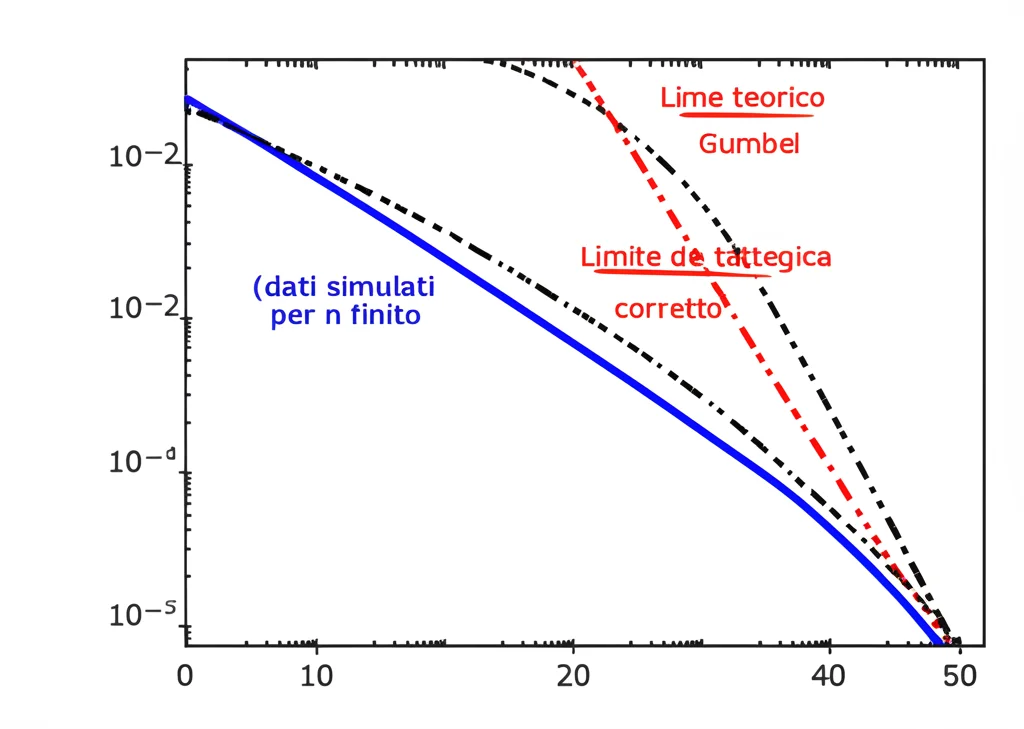
I risultati? La teoria regge! Le forme delle distribuzioni corrispondono. Tuttavia, le simulazioni ci mostrano anche che la convergenza verso il limite teorico può essere lenta. Per valori di *n* grandi ma non infiniti (come quelli che si usano in pratica), c’è spesso una piccola (o a volte non così piccola) discrepanza tra la simulazione e la Gumbel pura.
La buona notizia è che scavando nelle dimostrazioni matematiche, siamo riusciti a identificare i termini di “errore” principali, delle sorte di correzioni che dipendono da *n*. Aggiungendo queste correzioni alla Gumbel teorica, otteniamo una corrispondenza *molto* migliore con i dati simulati! Questo è utilissimo, perché ci permette di usare la teoria per fare previsioni accurate anche per numeri di punti finiti e realistici. Ad esempio, nel caso (d=2, k=1), la correzione più importante dipende dal perimetro dell’area e decresce lentamente (come (1/sqrt{log n})), spiegando perché la Gumbel “pura” non bastava.

In Conclusione: Un Puzzle di Punti e Confini

Quindi, la prossima volta che pensate a punti sparsi a caso, ricordate che c’è un mondo di matematica affascinante dietro. Capire come un insieme di punti ne copre un altro ci porta a esplorare le leggi dei valori estremi, come la distribuzione di Gumbel, e ci rivela l’importanza sorprendente dei confini geometrici, specialmente quando chiediamo livelli di copertura più stringenti. È un bellissimo esempio di come probabilità, geometria e analisi si intreccino per descrivere fenomeni apparentemente semplici ma ricchi di complessità. E le simulazioni ci aiutano a tenere i piedi per terra, assicurandoci che la nostra elegante teoria sia anche utile nel mondo reale!

Fonte: Springer