Gru a Ponte Sotto Controllo: La Mia Guida al Controllo Lineare Anti-Oscillazione

Ciao a tutti! Oggi voglio parlarvi di un argomento che mi appassiona molto e che è cruciale in tantissimi settori industriali: il controllo delle gru a ponte. Immaginate questi giganti meccanici che spostano carichi pesantissimi con precisione millimetrica. Affascinante, vero? Ma farle funzionare a dovere, specialmente quelle definite “sottoattuate”, è una sfida ingegneristica non da poco. Ecco perché ho deciso di sviluppare un approccio, una sorta di guida generalizzata, per progettare uno schema di controllo lineare che tenga a bada sia la posizione del carrello sia, soprattutto, quella fastidiosa oscillazione del carico.

La Sfida: Gru Sottoattuate e Oscillazioni Indesiderate

Perché è così complicato? Le gru a ponte sono spesso sistemi sottoattuati. In parole povere, significa che abbiamo meno “manopole” (attuatori) di quante ne servirebbero per controllare ogni singolo movimento (gradi di libertà). Nello specifico, di solito controlliamo direttamente solo il movimento orizzontale del carrello (la parte che scorre sulla trave), ma il carico appeso sotto oscilla come un pendolo, e non abbiamo un motore dedicato per fermare quell’oscillazione.

Il movimento del carrello e l’oscillazione del carico sono strettamente collegati (accoppiati) e le loro dinamiche sono intrinsecamente non lineari. Questo mix rende il controllo un bel rompicapo. Gli obiettivi principali sono sempre due:

• Posizionare il carrello esattamente dove serve.
• Ridurre al minimo (o eliminare del tutto) l’oscillazione del carico durante e alla fine del trasporto.

Il tutto, ovviamente, garantendo la sicurezza e cercando di essere il più veloci possibile. Esistono approcci a “ciclo aperto” (open-loop), ma in ambienti reali, con disturbi esterni (una folata di vento, un urto accidentale) e incertezze sui parametri (il peso esatto del carico, l’attrito), le strategie a “ciclo chiuso” (closed-loop), quelle che usano sensori per monitorare il sistema e correggere la rotta, sono decisamente preferibili. Ed è proprio su queste che mi sono concentrato.

Modellare per Capire: Dal Non Lineare al Lineare

Per progettare un buon controllore, la prima cosa da fare è capire a fondo come si comporta la gru. Qui entra in gioco la modellazione matematica. Ho utilizzato il formalismo di Euler-Lagrange per derivare un modello non lineare dettagliato, considerando la gru come un sistema carrello-pendolo (il cosiddetto modello a pendolo singolo, il più semplice ma efficace per molte applicazioni). Questo modello cattura tutte le complessità e le interazioni tra il movimento del carrello (coordinata x) e l’angolo di oscillazione del carico (coordinata θ).

Questo modello non lineare è preciso, ma usarlo direttamente per progettare controllori lineari (che sono più semplici da implementare e analizzare) è complicato. Quindi, il passo successivo è stato linearizzare il modello attorno a un punto di equilibrio. Qual è il punto di equilibrio di una gru? Semplice: carrello fermo in una posizione desiderata (x_d), carico perfettamente verticale (θ = 0°) e nessuna forza applicata (u = 0).

La linearizzazione ci fornisce equazioni differenziali lineari, che possiamo rappresentare facilmente con matrici (rappresentazione nello spazio degli stati) o, ancora più utile per il mio approccio, con le funzioni di trasferimento. Queste funzioni (una per la posizione del carrello X(s)/U(s) e una per l’angolo di oscillazione Θ(s)/U(s)) ci dicono come il sistema risponde a diverse frequenze di input. Analizzandole, emergono subito caratteristiche chiave:

• Mancanza di smorzamento intrinseco nell’oscillazione (poli immaginari puri).
• Presenza di frequenze critiche: una di risonanza (dove il sistema “amplifica” l’oscillazione) e una di anti-risonanza (dove il sistema sembra “cancellare” l’effetto dell’input sulla posizione del carrello a quella specifica frequenza).

Queste caratteristiche rendono evidente perché il controllo a ciclo chiuso è delicato: senza le giuste contromisure, il sistema può diventare instabile facilmente. Il modello lineare è un’ottima approssimazione vicino al punto di equilibrio, ma si discosta dal comportamento reale man mano che ci si allontana (ecco le “incertezze di modellazione” da gestire!).

Smorzamento Attivo: Calmare il Pendolo Senza Sensori Extra

Uno dei problemi principali è l’oscillazione persistente del carico dovuta alla mancanza di smorzamento naturale. Come fare? Ho introdotto una tecnica di smorzamento attivo. L’idea è usare l’attuatore del carrello non solo per spostarlo, ma anche per contrastare attivamente l’oscillazione. Molti approcci usano controllori PD (Proporzionale-Derivativo) per questo, ma l’azione derivativa pura può amplificare il rumore dei sensori.

La mia proposta si basa su una tecnica di retroazione di stato (state feedback). In teoria, misurando sia l’angolo θ che la sua velocità angolare θ̇, potremmo calcolare una forza di controllo aggiuntiva per “frenare” l’oscillazione. Il bello è che possiamo scegliere esattamente quanto smorzamento aggiungere (ho puntato a un comportamento sovrasmorzato, cioè senza oscillazioni residue).

Ma c’è un “ma”: misurare direttamente la velocità angolare θ̇ può essere difficile o costoso. Derivarla numericamente dall’angolo θ è rumoroso. La soluzione? Ho progettato un estimatore basato su filtro. In pratica, è un filtro passa-banda che stima θ̇ a partire da θ, replicando l’effetto derivativo alle frequenze che ci interessano ma attenuando il rumore ad alta frequenza. Funziona alla grande! Le simulazioni mostrano che questa tecnica, anche con l’estimatore, riduce le oscillazioni del carico di un impressionante 69.15% rispetto al caso senza smorzamento attivo, e senza bisogno di un sensore di velocità angolare dedicato.

Il Cuore del Sistema: I Controllori per Angolo e Posizione

Con lo smorzamento attivo in funzione, possiamo concentrarci sui controllori principali. Ne servono due, anche se abbiamo un solo input (la forza u sul carrello), che lavorano in sinergia.

1. Controllore dell’Angolo di Oscillazione (C_θ(s)): Questo controllore lavora sulla dinamica dell’angolo già “smorzata attivamente”. I suoi obiettivi sono:
* Assicurare che l’angolo θ tenda a zero (carico verticale).
* Compensare l’accoppiamento con la dinamica del carrello.
Ho scelto una struttura con un’azione integrale (per garantire precisione a regime, cioè errore nullo alla fine) e un compensatore lead (per migliorare la stabilità e la velocità di risposta). La messa a punto (tuning) è stata fatta analizzando la risposta in frequenza (diagrammi di Bode) per garantire buoni margini di stabilità (guadagno e fase). Un dettaglio: il guadagno di questo controllore è negativo per compensare certi segni nelle equazioni.

2. Controllore della Posizione del Carrello (C_x(s)): Questo è il controllore che porta il carrello alla posizione desiderata x_ref. Il suo design deve tenere conto della dinamica “vista” dal carrello, che include l’effetto del controllore dell’angolo e l’accoppiamento intrinseco. Analizzando il sistema con il solo C_θ(s) attivo, ho notato che la dinamica del carrello ha ancora quelle critiche frequenze di risonanza e anti-risonanza. Per garantire stabilità, precisione e un movimento fluido, ho optato per:
* Un’azione integrale (per precisione nonostante le non linearità residue).
* Ben due compensatori lead (per migliorare significativamente il margine di fase e la stabilità).
Anche qui, il tuning è basato sull’analisi in frequenza e sul luogo delle radici, cercando di ottenere una buona risposta senza eccitare le frequenze “pericolose”.

Movimenti Fluidi: Il Trucco del Pre-filtraggio

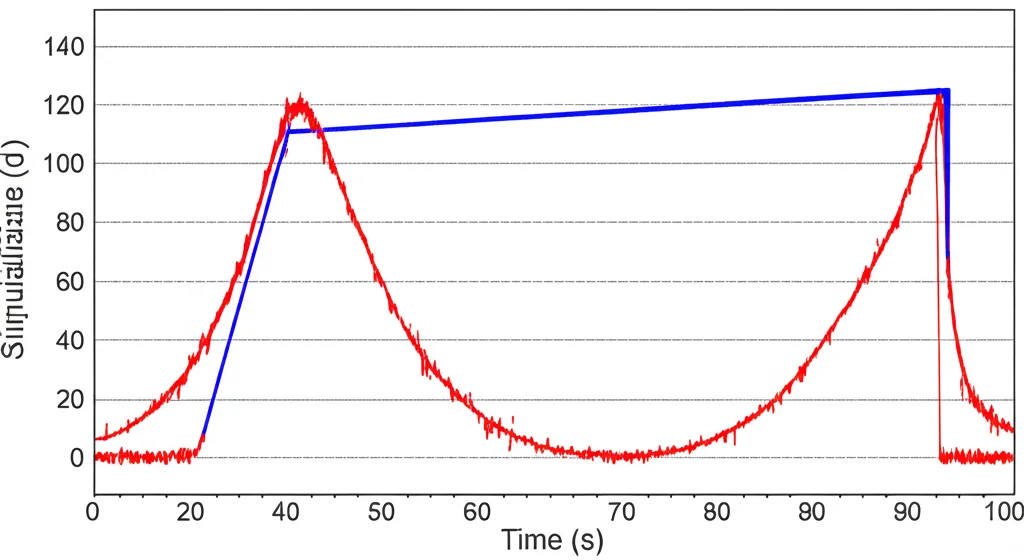
C’è un ultimo tassello fondamentale. Se diamo al controllore di posizione un comando “a gradino” (passa istantaneamente da 0 a 1 metro, per esempio), la risposta del sistema può essere brusca, con picchi di accelerazione che eccitano le risonanze e possono portare a instabilità o grandi oscillazioni.

La soluzione è il pre-filtraggio del riferimento di posizione. In pratica, invece di dare il comando x_ref direttamente al controllore C_x(s), lo facciamo passare attraverso un semplice filtro passa-basso del primo ordine. Questo filtro “smussa” il comando, trasformando un gradino in una rampa esponenziale dolce. Così facendo, il compito del controllore diventa seguire una traiettoria fluida (trajectory tracking) invece di raggiungere un set-point istantaneo. La banda passante di questo filtro va scelta con cura: abbastanza bassa da filtrare le frequenze problematiche, ma non così bassa da rendere il sistema troppo lento. Ho scelto una banda significativamente inferiore alla frequenza critica del margine di fase “pericoloso”.

Alla Prova dei Fatti: Robustezza a Disturbi e Incertezze

Un bello schema sulla carta è inutile se non funziona nel mondo reale. Per questo, ho messo alla prova l’intero sistema di controllo (con smorzamento attivo stimato, controllori C_θ e C_x, e pre-filtraggio) attraverso simulazioni realistiche usando il modello non lineare originale. Ho testato la sua robustezza in condizioni avverse:

• Rumore di misura: Ho aggiunto rumore casuale simulato ai sensori di posizione e angolo.
• Disturbi esterni: Ho applicato forze e coppie improvvise simulate sul carrello e sul carico (come una raffica di vento o un piccolo urto).
• Incertezze parametriche: Ho variato significativamente i parametri della gru rispetto a quelli usati per il tuning (massa del carico m e lunghezza del cavo L).

I risultati? Davvero incoraggianti! Anche con rumore, disturbi consistenti e parametri diversi da quelli nominali, lo schema di controllo è riuscito a portare il carrello a destinazione con precisione e a mantenere l’oscillazione del carico molto contenuta. Certo, le prestazioni transienti sono leggermente influenzate, ma il sistema rimane stabile e raggiunge gli obiettivi. Questo dimostra l’efficacia dell’approccio basato sull’analisi in frequenza e la scelta di adeguati margini di stabilità.

Conclusioni e Sguardo al Futuro

In sintesi, ho sviluppato un framework completo e, spero, abbastanza chiaro per progettare uno schema di controllo lineare per gru a ponte sottoattuate. L’approccio combina modellazione accurata, una tecnica di smorzamento attivo efficace (e senza sensori extra!), controllori lineari classici (ma ben giustificati e tarati con analisi in frequenza) e un pre-filtraggio intelligente del riferimento. Il risultato è un sistema robusto, capace di garantire precisione e stabilità anche in condizioni non ideali.

Certo, c’è sempre spazio per migliorare! Le direzioni future potrebbero includere:

• Tecniche per stimare anche l’angolo di oscillazione, eliminando pure quel sensore.
• Filtri più avanzati per gestire il rumore sul segnale di controllo finale, preservando gli attuatori.
• Estendere il framework a modelli di gru più complessi (es. doppio pendolo, cavi multipli).
• Introdurre tecniche adattive per auto-tarare i controllori in caso di grandi variazioni dei parametri.
• Sviluppare strategie esplicite per rigettare i disturbi esterni, migliorando ulteriormente la precisione.

Spero che questa panoramica vi abbia incuriosito e mostrato come, con un po’ di ingegneria dei controlli, si possano “domare” sistemi meccanici complessi come le gru a ponte!

Fonte: Springer