Il Segreto delle Bolle Danzanti: Come un Campo Elettrico Rivoluziona l’Ebollizione!

Ciao a tutti gli appassionati di scienza e tecnologia! Oggi voglio portarvi con me in un viaggio affascinante nel mondo microscopico, anzi, *mesoscopico*, per svelare come un pizzico di elettricità possa trasformare radicalmente un fenomeno comune come l’ebollizione. Parleremo di come i campi elettrici influenzano l’ebollizione libera (quella che in gergo chiamiamo “pool boiling”) di fluidi un po’ particolari, i cosiddetti fluidi dielettrici “imperfetti” o “con perdite” (leaky dielectric fluids). Sembra complicato? Tranquilli, cercherò di renderlo il più intrigante possibile!

Perché dovremmo interessarci all’ebollizione potenziata?

L’ebollizione è uno dei modi più efficienti che conosciamo per trasferire calore. Pensate ai sistemi di raffreddamento dei potenti componenti elettronici, agli scambiatori di calore industriali, o ai sistemi di gestione termica in ambito aerospaziale. Migliorare l’efficienza dell’ebollizione significa poter raffreddare meglio, rendere i sistemi più compatti o più potenti. Da decenni si cercano modi per “dare una spinta” a questo processo: superfici speciali, campi esterni… e tra questi, l’uso dei campi elettrici (che chiameremo ebollizione EF, da Electric Field) ha mostrato promesse incredibili.

Il mistero delle bolle: amiche o nemiche del campo elettrico?

Qui le cose si fanno interessanti. Molti studi hanno mostrato che applicando un campo elettrico, si formano più siti dove nascono le bolle (siti di nucleazione), le bolle si staccano quando sono più piccole e lo fanno più frequentemente. Sembra fantastico, no? Più bolle piccole e veloci dovrebbero significare più calore trasferito. E infatti, spesso è così, specialmente quando il liquido è molto surriscaldato o in assenza di gravità.

Ma c’era un paradosso! Alcuni esperimenti, concentrandosi sulla crescita di *una singola bolla*, mostravano l’esatto contrario: il campo elettrico sembrava *sopprimere* il distacco della bolla, rallentandolo. Come potevano essere vere entrambe le cose? E cosa succedeva con i fluidi dielettrici “imperfetti”, quelli che non sono isolanti perfetti ma nemmeno buoni conduttori (come l’acqua deionizzata o certi solventi organici), che sono stati studiati molto meno? Questi fluidi sono importanti in applicazioni come la separazione olio-acqua o i sistemi di protezione catodica.

La nostra lente d’ingrandimento: le simulazioni mesoscopiche

Per svelare questo mistero e capire a fondo la danza delle bolle sotto l’effetto di un campo elettrico, soprattutto in questi fluidi “leaky”, abbiamo deciso di usare uno strumento potentissimo: le simulazioni numeriche. Non simulazioni qualsiasi, ma simulazioni 3D su larga scala basate sul Metodo Lattice Boltzmann (LBM). L’LBM è un approccio mesoscopico, una via di mezzo tra il mondo atomico e quello macroscopico che vediamo tutti i giorni. Ci permette di modellare direttamente il cambiamento di fase (liquido-vapore) usando l’equazione di stato del fluido, senza troppi parametri empirici, e di includere le complesse forze elettrodinamiche (EHD) in gioco.

Abbiamo costruito un modello LBM unificato che integra il flusso EHD multifase, basato sul modello “leaky dielectric” (che considera sia la forza di Coulomb, dominante in questi fluidi, sia quella di polarizzazione). Immaginate un “acquario” virtuale rettangolare, riscaldato dal basso, riempito per due terzi di liquido dielettrico imperfetto. Nella metà inferiore applichiamo un campo elettrico verticale. Abbiamo poi osservato cosa succedeva al variare dell’intensità del campo elettrico (usando un numero adimensionale chiamato Numero di Capillarità Elettrico, Ca_e), della temperatura della superficie riscaldante (tramite il Numero di Jakob, Ja) e della conduttività elettrica del liquido (tramite il Numero di Rilassamento di Carica, T_σ). Le simulazioni erano enormi: oltre 250 milioni di celle computazionali, richiedendo decine di migliaia di ore CPU per ogni caso!

Risultati sorprendenti: il campo elettrico come “turbo” per l’ebollizione

I risultati sono stati illuminanti!

• Conferma dell’efficienza: Abbiamo confermato che l’ebollizione EF aumenta significativamente l’efficienza del trasferimento di calore, specialmente nel regime di ebollizione di transizione (quando la superficie è molto calda, ma non ancora completamente coperta da un film di vapore).
• Bolle più piccole e numerose: Proprio come osservato in molti esperimenti, applicando il campo elettrico abbiamo visto un aumento drastico del numero di bolle generate (fino a 5 volte di più!) e una riduzione significativa della loro dimensione media (fino al 50% più piccole). Anche i siti di nucleazione diventavano più numerosi e piccoli.
• Un modello predittivo: Basandoci sulla teoria idrodinamica (il modello di Berghmans, per i più tecnici), abbiamo sviluppato un modello teorico che predice accuratamente il flusso di calore medio (quanto calore viene trasferito) al variare dei parametri operativi, inclusa la conduttività elettrica. E funziona! Le nostre simulazioni combaciano perfettamente con le previsioni del modello.
• Addio all’ebollizione a film: Una delle scoperte più eccitanti è stata vedere come il campo elettrico possa contrastare l’ebollizione a film. Questo è un regime poco efficiente che si instaura a temperature molto alte, quando un film di vapore isolante copre la superficie calda, ostacolando il trasferimento di calore. Nei nostri test, anche a temperature dove normalmente si avrebbe ebollizione a film (Ja = 0.5), applicando il campo elettrico il sistema “tornava indietro” a un’ebollizione di transizione molto più efficiente, rompendo il film di vapore e generando nuovamente bolle attive!
• Il ruolo della conduttività: Abbiamo scoperto che aumentare la conduttività elettrica del liquido (cioè diminuire T_σ) potenzia ulteriormente l’effetto del campo elettrico. A parità di campo elettrico, un liquido leggermente più conduttivo mostrava un numero di bolle ancora maggiore (5-6 volte di più rispetto a un fluido quasi isolante) e un trasferimento di calore superiore (quasi il 30% in più). Questo suggerisce che, forse, modificare leggermente la conduttività del fluido (ad esempio aggiungendo ioni) potrebbe essere un modo economicamente vantaggioso per migliorare il raffreddamento.

Svelato l’arcano: l’effetto dimensionale della forza elettrica

Ma come fa il campo elettrico a fare tutto questo? E come si risolve il paradosso tra soppressione e potenziamento del distacco? La chiave sta nell’analizzare *dove* e *come* agisce la forza elettrica, e abbiamo scoperto che dipende crucialmente dalla dimensione!

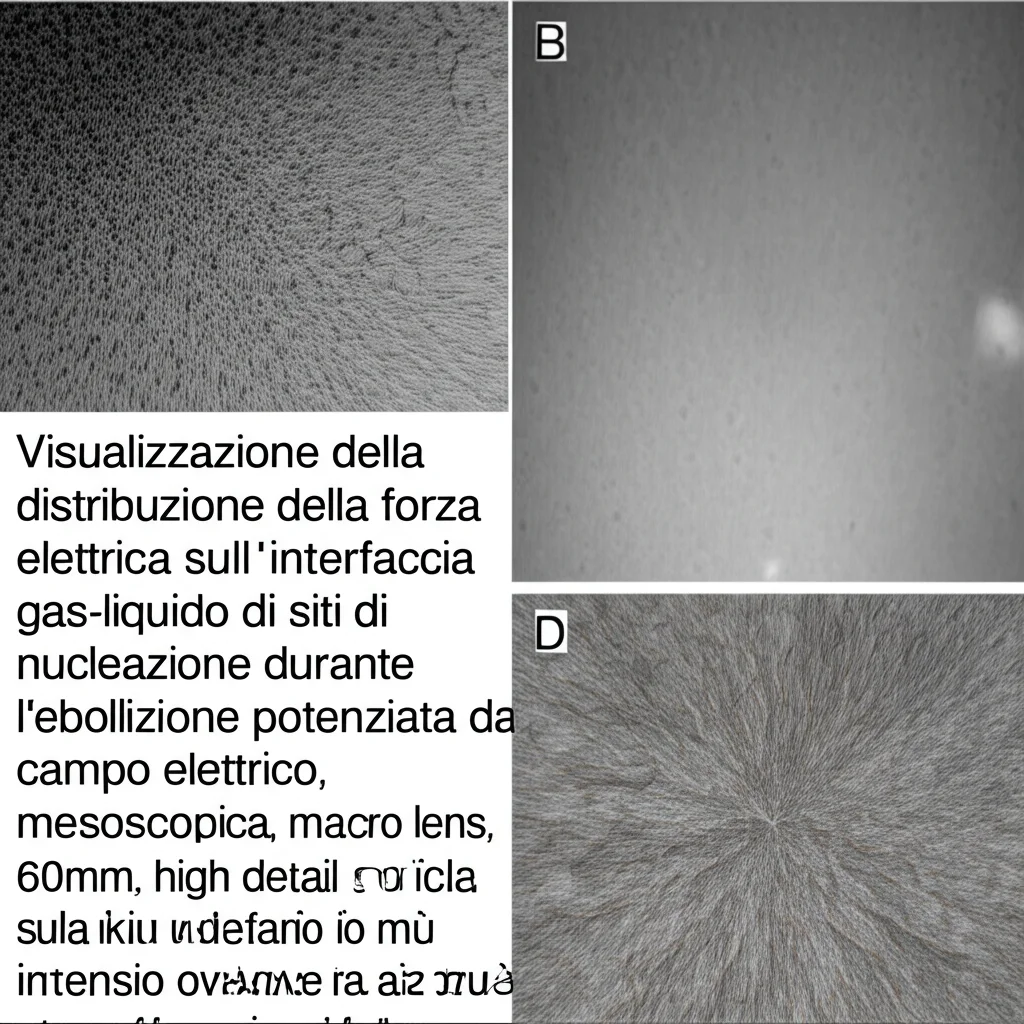
• Sui siti di nucleazione grandi: Abbiamo osservato che sui siti di nucleazione più estesi (dove il vapore forma quasi una pellicola continua sulla superficie), la forza elettrica si concentra lungo la linea dove si incontrano vapore, liquido e superficie solida (la linea di contatto tripla). Qui, la forza agisce comprimendo il vapore verso l’interno, quasi “strizzando” la base del sito. Questo effetto impedisce al film di vapore di staccarsi in un unico blocco e favorisce invece la frammentazione in bolle più piccole e monodisperse.
• Sui siti di nucleazione piccoli: Al contrario, sui piccoli siti isolati, la forza elettrica agisce su tutta la superficie della micro-bolla nascente, tendendo a inibirne la crescita iniziale. Infatti, con campi elettrici forti, questi siti più piccoli quasi scompaiono.
• Sulle bolle in risalita: Anche per le bolle che si sono già staccate e stanno risalendo nel liquido, l’effetto della forza elettrica dipende dalla dimensione. Per le bolle piccole (con raggio normalizzato R* < 0.51 circa), la forza elettrica è la forza dominante che le spinge. Per le bolle più grandi (R* > 0.51), invece, è la spinta di galleggiamento (la forza di Archimede) a prevalere.

Questa dipendenza dalla dimensione spiega il mistero! Negli esperimenti con singole bolle statiche o a crescita lenta, probabilmente dominava l’effetto inibitorio della componente verticale della forza o l’effetto sui piccoli siti. Nell’ebollizione libera reale (pool boiling), con tante bolle che interagiscono, prevale l’effetto compressivo sui siti più grandi e sulle bolle in crescita, che ne accelera la “strozzatura” (neck constriction) e il distacco, rendendole più piccole e frequenti. Le simulazioni su singola bolla in condizioni di ebollizione hanno confermato proprio questo: la forza elettrica comprime orizzontalmente la bolla, la allunga, riduce il diametro del “getto” di vapore alla base e, secondo la teoria dell’instabilità di Helmholtz, questo facilita la rottura e il distacco.

Conclusioni e prospettive future

In sintesi, il nostro viaggio mesoscopico ci ha permesso di capire molto meglio come i campi elettrici potenziano l’ebollizione nei fluidi dielettrici imperfetti. Abbiamo visto che:

• Aumentare l’intensità del campo elettrico o la conduttività del liquido migliora drasticamente il trasferimento di calore.
• Il campo elettrico può prevenire o invertire l’inefficiente ebollizione a film.
• Abbiamo sviluppato un modello teorico che predice bene il flusso di calore.
• Abbiamo svelato il meccanismo chiave: un effetto dimensionale della forza elettrica che spiega i comportamenti apparentemente contraddittori osservati in passato.

Certo, questo è solo l’inizio. Le simulazioni sono complesse e richiedono enormi risorse computazionali. Il prossimo passo sarà validare ulteriormente questi risultati con esperimenti mirati su fluidi reali e in un range ancora più ampio di condizioni operative. Ma la strada è tracciata: capire e controllare la danza delle bolle con i campi elettrici apre prospettive entusiasmanti per ottimizzare tantissime tecnologie che si basano sul trasferimento di calore per ebollizione. Spero di avervi trasmesso un po’ della mia fascinazione per questo campo di ricerca!

Fonte: Springer