Occhio al Bias! Come i Campioni Multipli Possono Ingannare le Tue Analisi Ecologiche

Ciao a tutti! Oggi voglio parlarvi di un argomento che mi sta molto a cuore e che riguarda un po’ tutti noi che lavoriamo con i dati, specialmente nel campo dell’ecologia, della salute pubblica o delle scienze sociali: l’analisi ecologica.

Cos’è l’Analisi Ecologica e Perché Dovrebbe Interessarci?

In parole povere, l’analisi ecologica è quella tecnica che usiamo quando vogliamo capire le relazioni complesse tra individui (o gruppi) e il loro ambiente, ma lo facciamo usando dati aggregati, a livello di gruppo. Pensate ai tassi di vaccinazione per regione e all’immunità media in quella stessa regione. Utile, vero? Soprattutto quando non abbiamo dati individuali che colleghino direttamente, ad esempio, la storia vaccinale di ogni singolo bambino con il suo stato di salute.

Ci sono diverse ragioni per cui ricorriamo a questo tipo di analisi:

• A volte, i dati a livello individuale semplicemente non esistono o non sono disponibili.
• Per eventi o malattie rare, i dati aggregati possono persino offrire maggiore accuratezza.
• Alcune domande di ricerca possono essere affrontate solo con tecniche di inferenza ecologica.

Negli ultimi vent’anni, c’è stato un vero boom di studi ecologici, grazie anche ai progressi nelle metodologie computazionali e statistiche che ci permettono di analizzare strutture di dati sempre più complesse.

Il Fantasma della Fallacia Ecologica (e Non Solo!)

Chiunque si sia avvicinato a questo campo ha sentito parlare della famigerata fallacia ecologica. È quel tranello logico per cui si applicano erroneamente a livello individuale le conclusioni tratte dai dati di gruppo. Il buon vecchio Robinson ci mise in guardia già decenni fa: non possiamo dare per scontato che le correlazioni osservate a livello di gruppo (ad esempio, tra reddito medio e tasso di criminalità in diverse città) riflettano fedelmente le relazioni a livello individuale (la relazione tra il reddito di una persona e la sua probabilità di commettere un crimine). Si assume, sbagliando, che ogni individuo nel gruppo abbia le caratteristiche medie del gruppo stesso.

Da allora, fiumi di inchiostro sono stati versati per capire le cause, le conseguenze e le possibili soluzioni a questo problema. Si è cercato di sviluppare metodi per “aggiustare” i dati ecologici e ottenere stime più corrette delle relazioni individuali. Spesso, per semplificare i modelli, si fa un’assunzione abbastanza forte: che gli individui all’interno di un gruppo siano indipendenti tra loro. Attenzione però, anche con questa assunzione, la fallacia ecologica può essere dietro l’angolo per altri motivi (variabilità ridotta nei gruppi, variabili omesse, ecc.).

La Scoperta: Un Nuovo Bias Legato ai Campioni Multipli

Ed è qui che entra in gioco la novità di cui voglio parlarvi oggi. Lavorando su questo tema, ci siamo accorti di un’altra fonte significativa di errore, un altro tipo di bias, che emerge quando si fa una cosa comunissima: usare dati aggregati provenienti da diversi dataset campionari. Immaginate di prendere i dati sulla copertura vaccinale da un’indagine campionaria e i dati sulla salute da un’altra indagine (magari condotta in un periodo diverso o con un campione diverso). Ecco, proprio qui si nasconde un problema.

Abbiamo scoperto che questo bias, che abbiamo chiamato “bias della frazione di campionamento” (sampling fraction bias), è direttamente proporzionale alla frazione di campionamento utilizzata per raccogliere i dati. In pratica, più piccola è la porzione di popolazione che includiamo nei nostri campioni, più questo bias può distorcere i risultati.

Perché succede? Semplificando un po’ le formule matematiche (che abbiamo derivato formalmente), il punto è che se prendiamo la media di una variabile X da un campione e la media di una variabile Y da un altro campione per lo stesso gruppo (es. la stessa città), la relazione (covarianza o coefficiente di regressione) tra queste due medie campionarie non è la stessa della relazione tra X e Y a livello individuale. Anzi, risulta “attenuata”, ridotta proprio da un fattore legato alla frazione di campionamento del campione da cui abbiamo preso la variabile indipendente (la X, nel nostro esempio).

Questo significa che, usando misure aggregate da campioni diversi, rischiamo sistematicamente di sottostimare la forza delle relazioni reali tra i fenomeni che stiamo studiando. E questo bias è presente anche se assumiamo che gli individui siano indipendenti tra loro, quindi non è la fallacia ecologica “classica”. È un problema aggiuntivo, e probabilmente altrettanto diffuso e importante!

Come Possiamo Correggere Questo Bias? Due Proposte

Ok, abbiamo identificato il problema. E ora? Non possiamo mica smettere di usare dati aggregati da fonti diverse, spesso sono gli unici disponibili! La buona notizia è che abbiamo anche proposto e testato due metodi per correggere questo bias:

1. Metodo dell’Inverso della Frazione di Campionamento (ISF – Inverse-Sampling-Fraction): L’idea qui è abbastanza intuitiva. Se il bias è legato alla frazione di campionamento (diciamo `sf_x`), possiamo provare a correggerlo “dividendo” il coefficiente di regressione che otteniamo dai dati aggregati proprio per `sf_x`. Matematicamente, abbiamo dimostrato che questo aggiustamento ci permette di stimare il coefficiente a livello individuale in modo più accurato.

2. Metodo Basato sui Modelli di Errore di Misurazione (MEA – Measurement-Error-Adjusted): Questo approccio è un po’ più sofisticato e si ispira ai lavori di Deaton sui pseudo-panel. Considera le medie campionarie come stime “rumorose” (cioè con un errore) delle vere medie della popolazione. Trattando la differenza tra media campionaria e media della popolazione come un errore di misurazione, possiamo usare le tecniche sviluppate per i modelli con errori di misurazione per ottenere una stima corretta della relazione di interesse.

La Prova dei Fatti: Simulazioni e Dati Reali

Naturalmente, non ci siamo fermati alla teoria. Abbiamo messo alla prova questi metodi. Prima, abbiamo creato dei dati simulati al computer, generando popolazioni con caratteristiche note e poi estraendo campioni multipli con diverse frazioni di campionamento. I risultati? Come previsto dalla teoria, il coefficiente di regressione calcolato sui dati aggregati campionari era sistematicamente più basso di quello reale (calcolato sui dati individuali o sulle medie dell’intera popolazione) e proporzionale alla frazione di campionamento. Ma, cosa più importante, entrambi i metodi di aggiustamento (ISF e MEA) sono riusciti a correggere efficacemente questo bias, riportando le stime molto vicine al valore vero.

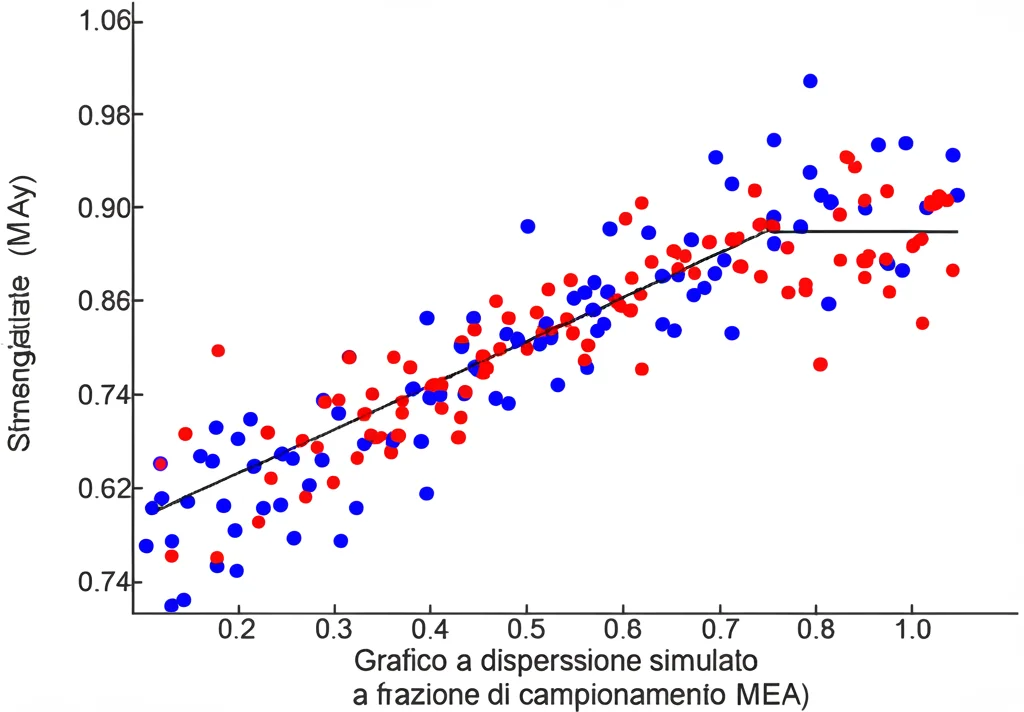
Poi, siamo passati al mondo reale. Abbiamo usato i dati del Kenya Demographic and Health Survey (DHS) del 2014. Questo è un sondaggio molto ampio e ben fatto, che ci ha permesso di trattare l’intero campione DHS come se fosse la nostra “popolazione” e poi di simulare l’estrazione di sotto-campioni multipli per analizzare la relazione tra il numero di figli di una donna (parità) e la durata della sua convivenza, aggregando i dati a livello di contea.

Anche qui, i risultati hanno confermato il problema: usando medie calcolate su campioni più piccoli (es. 20% del campione DHS totale), il coefficiente di regressione era significativamente più basso rispetto a quello calcolato usando le medie dell’intero “popolazione” DHS. Applicando i nostri metodi di correzione, abbiamo visto che funzionavano, ma con una sfumatura interessante: in questo contesto reale, il metodo MEA (quello basato sugli errori di misurazione) si è dimostrato particolarmente robusto e stabile, mentre il metodo ISF tendeva a “sovra-correggere” un po’. Questo suggerisce che il MEA potrebbe essere più affidabile quando si lavora con dati reali, che sono sempre un po’ più “disordinati” delle simulazioni.

Cosa Portiamo a Casa?

Il messaggio chiave che voglio lasciarvi è questo: dobbiamo essere molto cauti quando mettiamo insieme misure aggregate provenienti da campioni diversi nelle nostre analisi ecologiche. Il bias della frazione di campionamento è un rischio reale, concreto e potenzialmente molto diffuso (pensate a quante volte si usano dati da survey diverse, registri incompleti, ecc.). Questo bias si aggiunge alla già nota fallacia ecologica e può portare a conclusioni errate sulla forza delle relazioni che stiamo indagando.

Fortunatamente, abbiamo degli strumenti per affrontarlo. I metodi ISF e MEA che abbiamo proposto sembrano promettenti, specialmente il MEA per la sua robustezza. Certo, c’è ancora lavoro da fare per affinare questi metodi e capire come applicarli al meglio in tutte le situazioni (ad esempio, con variabili discrete o in modelli longitudinali, anche se pensiamo che il bias sia presente anche lì).

Quindi, la prossima volta che vi trovate a fare un’analisi ecologica combinando dati da più fonti campionarie, ricordatevi di questo potenziale “nemico nascosto”. Tenere conto del bias della frazione di campionamento e, se possibile, correggerlo, renderà le nostre inferenze più valide e le nostre conclusioni più solide. È un passo importante per migliorare l’accuratezza e l’affidabilità della ricerca in tantissimi campi, dalla salute pubblica alla sociologia all’economia. È un invito a tutta la comunità scientifica a essere più consapevoli e a sviluppare ulteriormente queste tecniche!

Fonte: Springer