Zeoliti Farneseite: Viaggio Affascinante nella Loro Topologia di Rete ed Entropia

Ciao a tutti! Oggi voglio portarvi con me in un viaggio affascinante nel mondo microscopico ma incredibilmente complesso delle zeoliti, in particolare quelle di tipo Farneseite (FAR). Magari vi state chiedendo: “Zeoliti? Che roba è?”. Beh, immaginate dei minerali super porosi, quasi delle spugne cristalline a livello atomico, con proprietà fisico-chimiche pazzesche. Sono così versatili che le troviamo un po’ ovunque: nell’industria chimica, nella medicina, per ripulire l’ambiente e persino in microelettronica.

Ma cosa rende le zeoliti così speciali?

Sono minerali microporosi con una struttura che sembra un labirinto tridimensionale fatto di atomi (principalmente silicio, alluminio, fosforo, collegati da ponti di ossigeno – li chiamiamo T-atomi). Questa struttura unica, fatta di canali e cavità di dimensioni precise, conferisce loro caratteristiche fantastiche:

• Stabilità termica elevata: Resistono bene al calore.
• Caratteristiche “accordabili”: Possiamo modificare la dimensione e la forma dei loro pori per adattarle a scopi specifici.
• Catalizzatori efficienti: Sono protagoniste nel “fluid catalytic cracking” (FCC), un processo che spezza molecole grandi di idrocarburi in benzina e diesel. Pensate a ZSM-5 e Y-zeoliti!
• Conduttori ionici: In certe condizioni, possono trasportare ioni, il che le rende utili per sensori e membrane a scambio ionico.
• Assorbimento selettivo: La loro struttura permette di “catturare” molecole specifiche, ad esempio per l’assorbimento di idrogeno (influenzato anche dagli anioni presenti).

I legami chimici al loro interno sono un mix interessante tra ionico e covalente, a seconda degli atomi coinvolti. Ad esempio, nei sistemi alluminofosfati prevale il carattere ionico, mentre nelle zeoliti di sola silice è più covalente. Si possono anche inserire metalli pesanti (Pd, Pt, Au…) per potenziare l’attività catalitica.

Focus sulla Farneseite (FAR)

La Farneseite è stata scoperta qui in Italia nel 2006. La sua formula è un po’ complessa: (Na,Ca,K)(_{56})(Al(_6)Si(_6)O(_{24}))(_7)(SO(_4))(_{12}).6H(_2)O. La sua struttura è formata da tetraedri TO(_4) (con T = Si o Al) che condividono gli spigoli. Ha una struttura esagonale con due tipi di canali: uno più largo formato da anelli a 12 membri (12MR) e uno più stretto, ellittico, da anelli a 8 membri (8MR).
Ha una densità di impacchettamento atomico (esclusi i pori) di 17.1 T/1000 Å(^3) e una densità topologica di 0.693 nodi/nm(^3). Questi numeri ci danno un’idea di quanto sia “compatta” e connessa la sua struttura interna. È interessante notare che si possono sintetizzare strutture simili (ZIFs, Zeolite Imidazole Frameworks) usando metalli di transizione (Zn, Co) al posto di Al/Si, ottenendo materiali ancora più stabili.

Come studiamo queste strutture intricate? La Teoria dei Grafi ci dà una mano!

Capire la complessità di queste reti atomiche è una bella sfida. Qui entra in gioco la teoria dei grafi, una branca della matematica che studia le reti (grafi), fatte di nodi (nel nostro caso, gli atomi T) e archi (i legami tra loro, mediati dall’ossigeno). Possiamo usare la teoria dei grafi per:

• Descrivere la topologia: Capire come sono connessi gli atomi e confrontare diverse strutture.
• Studiare le transizioni di fase: Analizzare come la struttura cambia sotto calore o pressione.
• Analizzare i “vicinati”: Comprendere come la forma locale della rete influenzi l’adsorbimento di molecole o la catalisi all’interno dei pori.

Per quantificare queste caratteristiche strutturali, usiamo dei numeri speciali chiamati indici topologici. Questi indici si basano sulle distanze tra gli atomi nella rete o sul numero di connessioni di ciascun atomo. Sono strumenti potentissimi negli studi QSPR/QSAR (Quantitative Structure-Property/Activity Relationship), che cercano di prevedere le proprietà fisiche o l’attività biologica di materiali e composti chimici basandosi sulla loro struttura.

La sfida dei calcoli e il “Metodo dei Tagli”

Calcolare questi indici, specialmente quelli basati sulle distanze tra *tutte* le coppie di atomi, può diventare un incubo computazionale per strutture grandi e complesse come le zeoliti. Immaginate di dover misurare la distanza più breve tra ogni coppia di punti in un labirinto 3D enorme!
Per fortuna, nel nostro studio (quello citato nel testo originale), abbiamo usato un approccio più furbo: il “metodo dei tagli” (cut method). Questo metodo sfrutta una proprietà matematica di queste reti (sono “cubi parziali”) che ci permette di “affettare” virtualmente la struttura in modi specifici (usando la relazione (Theta) di Djoković-Winkler) e analizzare le parti risultanti. È come smontare un meccanismo complesso pezzo per pezzo per capirne il funzionamento generale, ma in modo matematicamente rigoroso. Questo semplifica enormemente i calcoli!
Grazie a questo metodo, siamo riusciti a derivare delle formule generali per calcolare vari indici topologici basati sulla distanza (come gli indici di Wiener, Szeged, Padmakar-Ivan, Mostar nelle loro varianti vertice, arco e vertice-arco) per la rete della Farneseite, rappresentata come FAR(p,q), dove p e q indicano le dimensioni della “mattonella” di celle unitarie che si ripete per formare la struttura.

Entropia: Misurare la Complessità della Rete

Oltre agli indici, un altro concetto chiave che abbiamo esplorato è l’entropia. Non pensate subito al disordine termodinamico! Qui parliamo di entropia informazionale di Shannon, applicata ai grafi. È una misura che quantifica la complessità o il “disordine informativo” della struttura della rete. Più alto è il valore, più complessa o “disordinata” (in senso informativo) è la rete.
Abbiamo calcolato l’entropia basata su alcuni indici topologici (in particolare quelli di tipo Szeged e Padmakar-Ivan). Perché questi e non altri? Beh, l’indice di Wiener non si presta direttamente, mentre l’indice di Mostar può dare problemi matematici (valori nulli o indeterminati). L’entropia basata sulla distanza, anche se più complessa da calcolare rispetto a quella basata solo sulle connessioni locali (grado dei vertici), ci dà una visione più completa della struttura globale della rete, catturando come le informazioni si “spargono” al suo interno.
Abbiamo calcolato questi valori di entropia per strutture di Farneseite quadrate (FAR(p,p)) di dimensioni crescenti. È interessante notare che, essendo l’entropia una funzione logaritmica, i valori tendono a stabilizzarsi abbastanza rapidamente: la complessità essenziale viene catturata già a dimensioni relativamente piccole.

Farneseite (FAR) vs Sodalite (SOD): Un Confronto di Complessità

La Farneseite appartiene al gruppo cancrinite-sodalite. Era quindi naturale confrontare la sua complessità con quella della Sodalite (SOD), un’altra zeolite ben nota la cui topologia era già stata studiata con metodi simili. Per fare un confronto equo, abbiamo calcolato l’entropia “scalata”, cioè l’entropia divisa per il numero totale di legami nella struttura.
E qui arriva il risultato affascinante: le reti di tipo Sodalite (SOD) mostrano un’entropia scalata maggiore rispetto a quelle di tipo Farneseite (FAR). Cosa significa? Suggerisce che la struttura della SOD ha un grado maggiore di “disordine informativo” o complessità topologica rispetto alla FAR. La Farneseite sembra avere una disposizione atomica più compatta e organizzata, con atomi più vicini tra loro, risultando in un’entropia topologica inferiore. La SOD, invece, ha una topologia più irregolare, specialmente in periferia, che si traduce in un’entropia maggiore. Queste differenze topologiche potrebbero avere implicazioni importanti, ad esempio, nel modo in cui queste strutture si trasformano da una forma all’altra (transizioni di fase).

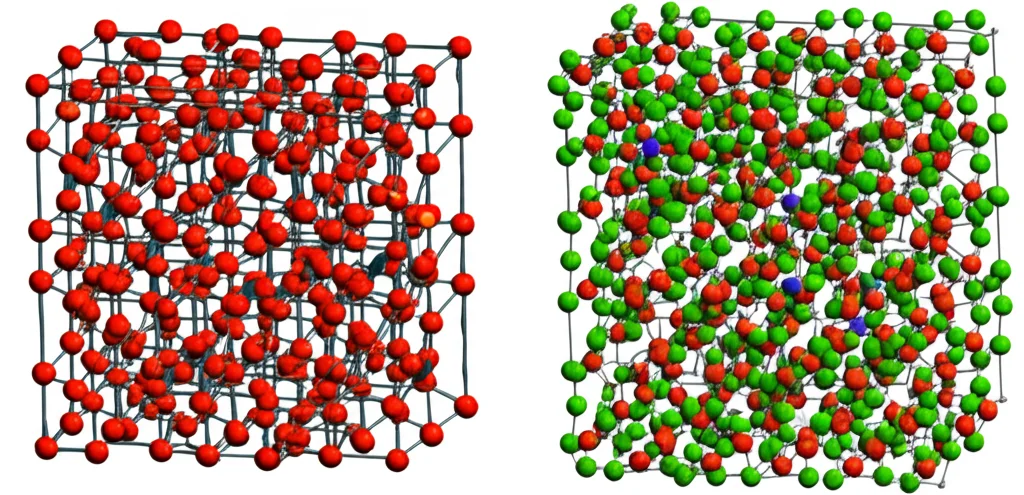
Perché tutto questo è importante?

Questo studio, che combina teoria dei grafi, indici topologici ed entropia, ci fornisce strumenti potenti per decifrare la complessità nascosta nelle strutture delle zeoliti come la Farneseite. Questi descrittori numerici non sono solo un esercizio matematico:

• Possono essere usati in futuro per prevedere le proprietà dei materiali (studi QSAR/QSPR).
• Aiutano a capire le differenze fondamentali tra diverse famiglie di zeoliti (come FAR e SOD) e come queste differenze possano influenzare il loro comportamento, ad esempio durante le transizioni di fase.
• Aprono la strada all’integrazione con approcci moderni come il machine learning e le simulazioni quantistiche (come la DFT su blocchi più piccoli), per creare modelli predittivi sempre più accurati delle proprietà di queste affascinanti strutture.

Insomma, analizzare la topologia e l’entropia delle zeoliti è come avere una mappa speciale per navigare la loro architettura interna e svelarne i segreti. E chissà quali nuove applicazioni e scoperte ci riserva il futuro grazie a questa comprensione più profonda!

Fonte: Springer