Modelli Idrologici e Incertezza: Come il PCK Rivoluziona le Simulazioni di Ruscellamento ed Erosione

Ciao a tutti! Oggi voglio parlarvi di una sfida affascinante nel mondo della modellistica ambientale: come facciamo a prevedere quanta acqua scorrerà via (il ruscellamento) e quanto suolo verrà eroso dopo una pioggia, specialmente quando i nostri modelli sono super complessi e pieni di incertezze? È un bel rompicapo, credetemi!

Il Problema: Modelli Complessi e l’Incubo dell’Incertezza

Noi scienziati usiamo quelli che chiamiamo modelli basati sui processi (PBMs). Sono strumenti potentissimi perché cercano di simulare la fisica reale dietro a fenomeni come l’infiltrazione dell’acqua nel suolo, il suo scorrimento in superficie e il trasporto dei sedimenti. Pensate a modelli come tRIBS-VEGGIE-FEaST, che abbiamo usato in questo studio: sono incredibilmente dettagliati.

Il problema? Questi modelli hanno un sacco di “manopole” da regolare, i cosiddetti parametri (come la conducibilità idraulica del suolo, la sua composizione in argilla, sabbia, etc.). Trovare i valori giusti è difficile, e spesso c’è molta incertezza. Inoltre, far girare una singola simulazione può richiedere ore, se non giorni, su potenti computer. Ora immaginate di dover fare migliaia di simulazioni per capire come l’incertezza sui parametri influenzi i risultati… un incubo computazionale!

Metodi tradizionali come le simulazioni Monte Carlo, che richiedono appunto tantissime “run”, diventano impraticabili. Certo, si può provare a ottimizzare il codice o usare supercomputer, ma non è sempre la soluzione ideale o accessibile.

La Soluzione Geniale: Il Surrogate Modeling e il PCK

Ed è qui che entra in gioco la nostra idea: usare i modelli surrogati. Cosa sono? Immaginate di avere una Ferrari (il nostro modello PBM super dettagliato ma lento) e di voler creare un go-kart velocissimo (il modello surrogato) che però riesca a imitare il comportamento della Ferrari in modo sorprendentemente accurato, almeno per quello che ci serve sapere.

Il nostro “go-kart” preferito si chiama Polynomial Chaos Kriging (PCK). È una tecnica che combina due approcci potenti: l’espansione del caos polinomiale (che cattura le tendenze globali del modello) e il Kriging (che si occupa delle variazioni locali e fornisce stime dell’incertezza). È come avere il meglio di due mondi: un modello che apprende la “visione d’insieme” e allo stesso tempo è bravo nei dettagli locali. Il risultato? Un surrogato che non solo è veloce, ma spesso è più accurato dei singoli metodi da cui deriva!

Abbiamo quindi deciso di applicare il PCK al nostro modello tRIBS-VEGGIE-FEaST per vedere se riusciva a gestire la complessità della simulazione simultanea di ruscellamento ed erosione del suolo.

Mettiamolo alla Prova: Uno Studio Sintetico

Per testare il tutto, abbiamo creato uno scenario “sintetico”, basato su dati reali raccolti in un sito sperimentale classico per lo studio dell’erosione (Clarinda, Iowa). Abbiamo preso un evento di pioggia specifico e simulato cosa sarebbe successo su un piccolo appezzamento di terreno virtuale.

Abbiamo identificato 9 parametri chiave del modello tRIBS-VEGGIE-FEaST legati al ruscellamento (come la conducibilità idraulica satura, Ks) e all’erosione (le frazioni delle diverse dimensioni delle particelle di suolo: argilla, limo, sabbia…).

Il nostro framework unificato prevedeva tre passi:

• Usare il PCK per creare il surrogato super-veloce del modello originale.
• Utilizzare la tecnica GLUE (Generalized Likelihood Uncertainty Estimation), un approccio Bayesiano “informale”, per capire quali combinazioni di parametri davano risultati “accettabili” (vicini ai dati osservati di ruscellamento e perdita di suolo totali).
• Applicare l’analisi di sensibilità globale di Sobol’ per scoprire quali parametri avessero l’impatto maggiore sui risultati e come interagissero tra loro.

Abbiamo generato ben 100.000 (!) set di parametri diversi usando una tecnica chiamata Latin Hypercube Sampling per esplorare a fondo lo spazio delle possibilità.

Risultati Sorprendenti: Velocità, Precisione e Scoperte sull’Incertezza

E i risultati? Davvero notevoli!

Prima di tutto, il PCK si è dimostrato un emulatore fantastico. Abbiamo confrontato 10.000 simulazioni fatte con il modello originale e con il surrogato PCK: i risultati erano praticamente identici, con un R² vicino a 1! La differenza sta nel tempo: il PCK ha impiegato circa 5 secondi per fare ciò che al modello originale (anche usando il calcolo parallelo) avrebbe richiesto circa 40 ore (e senza parallelizzazione, staremmo parlando di 20.000 ore!). Una riduzione di tempo pazzesca!

Secondo, l’analisi dell’incertezza ha rivelato quanto questa possa essere grande. L’errore sul volume totale (VE) poteva arrivare fino al 300% per il ruscellamento e addirittura all’800% per la perdita di suolo! Questo ci dice che, senza un’analisi accurata, le previsioni del modello potrebbero essere molto lontane dalla realtà. Delle 100.000 simulazioni, solo 892 sono rientrate nella soglia di “accettabilità” che avevamo fissato (VE < 10% per entrambi gli output). Questo sottolinea l'importanza di poter generare tantissime simulazioni rapidamente, cosa possibile solo grazie al surrogato.

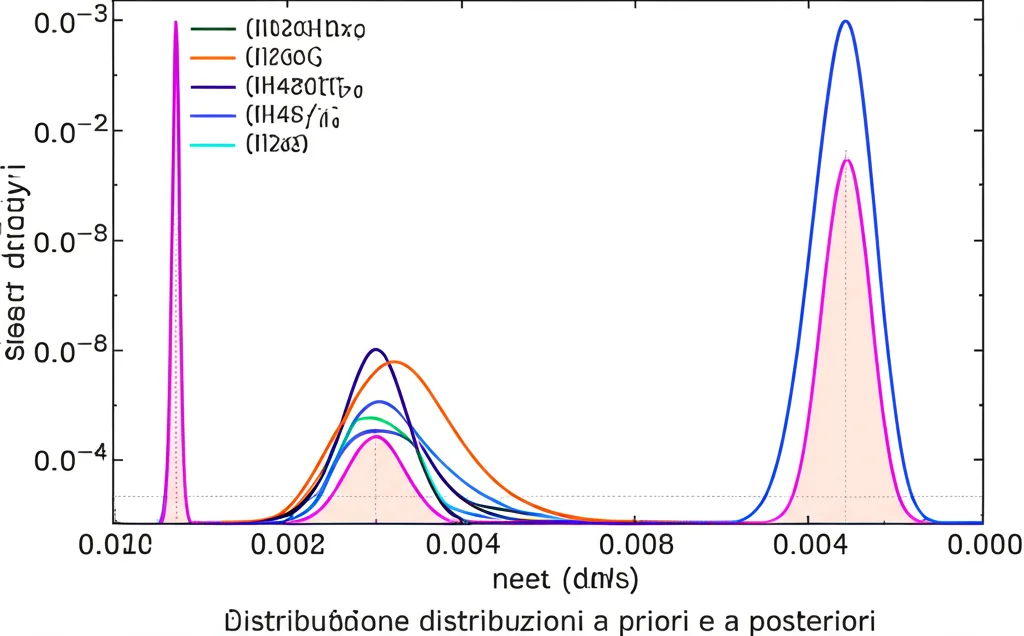
Terzo, l’analisi di sensibilità ha fatto luce sui “protagonisti”. Il parametro più influente per entrambi, ruscellamento e perdita di suolo, è risultato essere la conducibilità idraulica satura (Ks). Per la perdita di suolo, anche la frazione di argilla (Fc) gioca un ruolo significativo. È interessante notare che la sensibilità di questi parametri non è costante, ma varia nel tempo durante l’evento di pioggia, raggiungendo il picco nei momenti di massima intensità.

Infine, abbiamo osservato una forte equifinalità: molte combinazioni diverse di parametri (ad eccezione di Ks, che doveva essere in un range più ristretto) potevano produrre risultati finali simili e accettabili. Questo è importante perché suggerisce che potremmo concentrare gli sforzi di calibrazione del modello solo sui parametri veramente cruciali, risparmiando tempo.

Abbiamo anche confrontato il PCK con altri modelli surrogati popolari (Gaussian Process Regression e Random Forest). Il PCK si è dimostrato superiore nel catturare i valori estremi (i picchi di ruscellamento ed erosione), un aspetto fondamentale in molte applicazioni pratiche.

Cosa Significa Tutto Questo? Implicazioni e Prospettive Future

Questo framework che integra PCK, GLUE e analisi di sensibilità offre un modo robusto ed efficiente per affrontare l’incertezza nei modelli PBM complessi. I vantaggi sono enormi:

• Risparmio Computazionale Drastico: Rende fattibile l’analisi di incertezza anche per modelli molto pesanti.
• Migliore Comprensione del Modello: Ci aiuta a capire quali parametri contano davvero e come interagiscono.
• Quantificazione dell’Incertezza: Fornisce una stima realistica del range di possibili risultati, fondamentale per prendere decisioni informate (es. pianificazione territoriale, gestione del rischio idrogeologico, strategie di adattamento al cambiamento climatico).
• Potenziale per Previsioni in Tempo Reale: La velocità del surrogato apre le porte all’uso di questi modelli complessi anche per previsioni operative.

Sebbene questo studio fosse sintetico, la metodologia è assolutamente applicabile a casi reali, a patto di configurare correttamente il modello originale con dati specifici del sito (topografia, suolo, vegetazione). Il prossimo passo sarà proprio testarlo su bacini idrografici reali.

In conclusione, abbiamo dimostrato come l’uso intelligente dei modelli surrogati, in particolare il PCK, possa trasformare il modo in cui analizziamo l’incertezza nei modelli ambientali, rendendo le nostre simulazioni più veloci, affidabili e utili per affrontare le sfide legate all’acqua e al suolo.

Fonte: Springer