Crepe nei Materiali Piezoelettrici: Quando la Scienza Incontra l’Intelligenza Artificiale!

Ciao a tutti, appassionati di scienza e tecnologia! Oggi voglio parlarvi di qualcosa che mi affascina moltissimo: i materiali piezoelettrici e un problema un po’ spinoso che li riguarda, ovvero le crepe, in particolare quelle rettangolari. Perché sono importanti? Beh, questi materiali sono delle piccole meraviglie: convertono la pressione meccanica in energia elettrica e viceversa. Li troviamo ovunque: sensori, attuatori, dispositivi medici, persino in sistemi per raccogliere energia dall’ambiente (energy harvesting). Fantastico, no?

Però, come tutte le cose belle, hanno un punto debole. Durante il loro utilizzo, possono essere sottoposti a stress meccanici e campi elettrici che, ahimè, possono portare alla formazione e alla propagazione di crepe. E una crepa, soprattutto una bella crepa rettangolare interna, può compromettere seriamente le loro proprietà meccaniche ed elettriche, mettendo a rischio l’affidabilità e il funzionamento dei dispositivi che li utilizzano. Immaginate un sensore medico che smette di funzionare correttamente a causa di una micro-crepa… non è proprio il massimo!

Perché Focalizzarsi sulle Crepe Rettangolari?

Molti studi si sono concentrati sulle crepe bidimensionali, analizzando come si comportano, quali sono i fattori di intensità dello stress (SIF) sulla punta della crepa, quanta energia viene rilasciata quando si propagano. Ma la realtà, spesso, è tridimensionale. Le crepe rettangolari in 3D sono più complesse da studiare a causa della loro geometria e degli effetti di accoppiamento multidimensionale tra campo meccanico ed elettrico sulla punta della crepa.

Capire come si comportano queste crepe specifiche è fondamentale. Da un lato, ci aiuta a comprendere più a fondo il comportamento a frattura di questi materiali in condizioni operative reali (accoppiamento elettro-meccanico). Dall’altro, ci fornisce strumenti preziosi per progettare meglio i dispositivi, ottimizzarne le prestazioni e gestirne la durata. Insomma, studiare le crepe rettangolari 3D è un passo avanti importante nella meccanica della frattura dei materiali piezoelettrici.

La Teoria Dietro le Quinte: Equazioni e Modelli

Per affrontare il problema, siamo partiti dalle basi: la teoria. Abbiamo stabilito le equazioni che governano l’accoppiamento elettro-meccanico e le relazioni costitutive dei materiali piezoelettrici. In pratica, si tratta di formule matematiche che descrivono come lo stress (forza) e lo spostamento elettrico (campo elettrico) si influenzano a vicenda all’interno del materiale, specialmente vicino alla punta della crepa.

Abbiamo considerato un materiale piezoelettrico con una crepa rettangolare al suo interno (immaginatela posizionata sull’asse z=0, con dimensioni definite lungo x e y). Usando la termodinamica e l’ipotesi di piccole deformazioni, abbiamo derivato le equazioni costitutive 3D per il tensore dello stress e il vettore di spostamento elettrico. Queste equazioni mettono in relazione stress, deformazione, campo elettrico e spostamento elettrico attraverso le costanti del materiale (elastiche, piezoelettriche e dielettriche).

Poi, abbiamo impostato le condizioni al contorno: cosa succede sulla superficie della crepa e lontano da essa? Sulla crepa, lo stress deve essere nullo (è una superficie libera), mentre lontano dalla crepa, il materiale è considerato a riposo meccanico. Risolvere questo sistema di equazioni differenziali alle derivate parziali con queste condizioni al contorno ci permette, in teoria, di calcolare il campo di stress e il campo di spostamento elettrico ovunque nel materiale, e in particolare vicino alla punta della crepa, che è la zona critica per la propagazione. Per farlo, abbiamo usato tecniche matematiche come le trasformate di Fourier e l’introduzione di funzioni ausiliarie per semplificare i calcoli. Lo so, può sembrare complicato, ma è il cuore teorico che ci permette di prevedere il comportamento del materiale!

Simulazioni al Computer: Vedere per Credere

La teoria è fondamentale, ma per avere una visione più concreta e analizzare scenari complessi, ci siamo affidati alle simulazioni numeriche, usando il metodo degli elementi finiti (FEM). Abbiamo utilizzato un software potente come ABAQUS, che è ottimo per simulare problemi di accoppiamento come quello elettro-meccanico.

Abbiamo costruito un modello 3D di una piastra di materiale piezoelettrico con una crepa rettangolare al centro. Per semplificare, data la simmetria del problema, abbiamo analizzato solo metà della piastra. Abbiamo definito le proprietà del materiale (in questo caso, abbiamo usato PZT-4 e PZT-5H, due comuni ceramiche piezoelettriche) e applicato diversi carichi: solo una forza di trazione (stress meccanico) oppure una combinazione di forza e campo elettrico (carico elettro-meccanico).

Cosa abbiamo osservato? I risultati sono stati illuminanti!

• Concentrazione dello Stress: Come previsto dalla teoria, la punta della crepa è la zona dove lo stress è massimo. È qui che il materiale è più sollecitato e da dove la frattura tende a partire.
• Effetto del Carico Meccanico: Applicando solo una forza di trazione (ad esempio, 1 MPa, 2 MPa, 8 MPa sul PZT-4), abbiamo visto che all’aumentare del carico, aumentano sia lo stress massimo sulla punta della crepa sia lo spostamento (la deformazione) del materiale. È interessante notare che anche senza applicare un campo elettrico esterno, si genera comunque una differenza di potenziale elettrico attorno alla crepa. Questo è l’effetto piezoelettrico diretto in azione: lo stress meccanico induce una risposta elettrica!
• Confronto tra Materiali: Abbiamo ripetuto le simulazioni con il PZT-5H (applicando 5 MPa e 7 MPa). Anche se le proprietà piezoelettriche di PZT-4 e PZT-5H sono diverse, il trend generale è simile: lo stress aumenta con il carico. Ovviamente, i valori specifici di stress e potenziale cambiano a seconda del materiale.
• Effetto del Carico Elettro-Meccanico: Qui le cose si fanno ancora più interessanti. Abbiamo applicato una forza di 5 MPa sul PZT-5H e aggiunto un campo elettrico (prima +2000 V/m, poi -2000 V/m). Abbiamo visto che il campo elettrico modifica la distribuzione di stress e spostamento rispetto al caso con solo carico meccanico. Un campo elettrico positivo e uno negativo hanno effetti diversi: uno può favorire la propagazione della crepa, l’altro può ostacolarla. Tuttavia, nelle condizioni simulate, l’influenza del carico meccanico sulla crescita della crepa sembrava essere predominante rispetto a quella del campo elettrico applicato.
• Zona di Danno: Le simulazioni mostrano chiaramente che il danno (rappresentato dall’alto stress) è concentrato vicino alla punta della crepa e diminuisce man mano che ci si allontana, specialmente verso gli angoli della crepa rettangolare. La dimensione di quest’area danneggiata dipende dall’intensità del carico applicato.

L’Asso nella Manica: Machine Learning per Capire di Più

E qui arriva la parte che ritengo davvero innovativa di questo studio. Per la prima volta, abbiamo applicato tecniche di machine learning, specificamente il Random Forest e la Metodologia della Superficie di Risposta (RSM), all’analisi delle crepe rettangolari nei materiali piezoelettrici.

Abbiamo usato il Random Forest, un algoritmo di apprendimento automatico, per creare modelli di regressione capaci di predire i valori di stress e spostamento sulla base dei dati ottenuti dalle simulazioni. Abbiamo “addestrato” il modello e poi lo abbiamo testato. I risultati? Ottimi! I grafici dei residui (la differenza tra valori reali e predetti) mostrano che le previsioni sono molto accurate, con coefficienti di correlazione superiori a 0.9 per stress e spostamenti. Questo significa che il modello di machine learning ha “imparato” bene le relazioni complesse tra i parametri.

Poi, abbiamo usato la RSM, in particolare il disegno Box-Behnken (BBD), per analizzare come tre fattori chiave – la lunghezza della crepa (A), il carico meccanico (B) e il campo elettrico (C) – influenzano le risposte (stress S, spostamenti U1 e U3) nel materiale PZT-5H. L’analisi statistica (ANOVA) ha confermato che tutti e tre i fattori, così como le loro interazioni, hanno un effetto statisticamente molto significativo (p-value < 0.0001) sulle risposte. 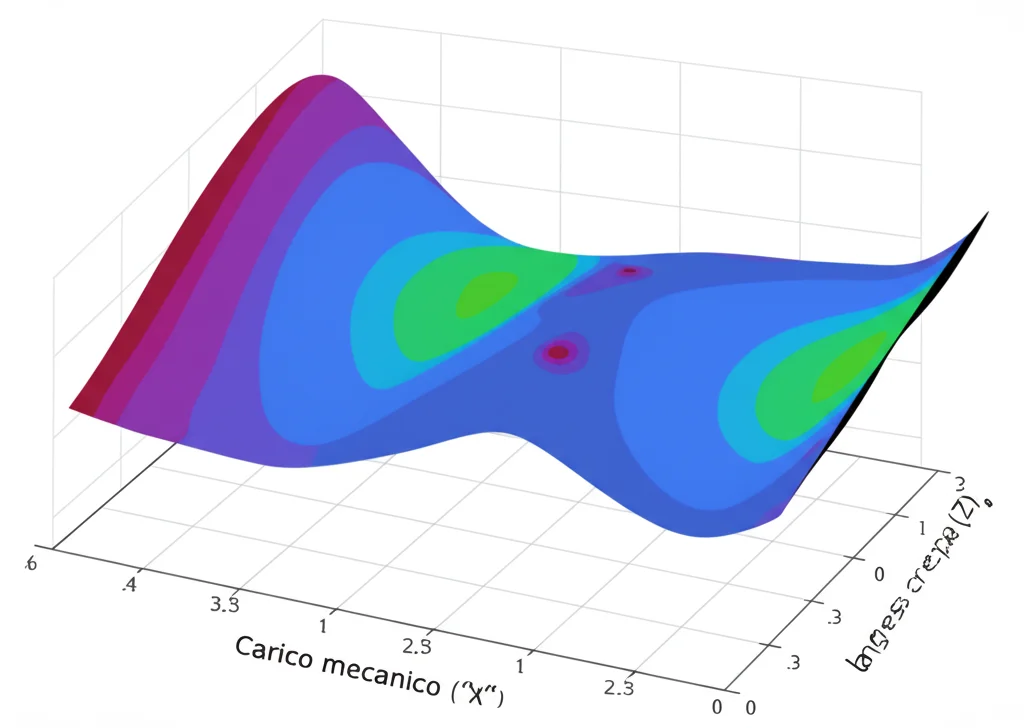La RSM ci ha permesso non solo di capire quali fattori sono più influenti, ma anche di creare delle "mappe" (le superfici di risposta) che mostrano visivamente come le risposte cambiano al variare dei fattori. Ad esempio, possiamo vedere come lo stress sulla punta della crepa aumenta sia con la lunghezza della crepa sia con il carico meccanico. Ancora più utile, la RSM ci ha permesso di trovare le condizioni "ottimali" per ottenere determinati valori target. Ad esempio, per massimizzare lo stress (che potrebbe essere utile in alcune applicazioni di sensoristica, o da minimizzare per la sicurezza strutturale), abbiamo trovato che con una crepa di 20 mm, un carico di 10 MPa e un campo di 4000 V/m si ottiene un valore S elevato. Similmente, abbiamo trovato le condizioni per massimizzare o minimizzare gli spostamenti U1 e U3.

Conclusioni e Sguardo al Futuro

Quindi, cosa ci portiamo a casa da questo viaggio tra crepe e piezoelettricità?

• Abbiamo analizzato in dettaglio, sia teoricamente che con simulazioni, il comportamento complesso delle crepe rettangolari 3D nei materiali piezoelettrici.
• Abbiamo confermato che lo stress si concentra sulla punta della crepa e che sia il carico meccanico sia il campo elettrico influenzano significativamente stress, spostamento e potenziale elettrico.
• Abbiamo visto che materiali diversi (PZT-4, PZT-5H) mostrano comportamenti simili ma con magnitudini diverse.
• L’applicazione del machine learning (Random Forest e RSM) si è rivelata un successo, fornendo modelli predittivi accurati e permettendo un’analisi approfondita dell’influenza dei parametri chiave. Questa è la vera novità!

Questo lavoro apre le porte a future ricerche. Sarebbe interessante studiare come altri parametri del materiale (coefficiente piezoelettrico, costante dielettrica, costanti elastiche) influenzino il comportamento delle crepe. Inoltre, si potrebbe passare a simulazioni multi-scala, che combinino gli effetti macroscopici con quelli microscopici (come la polarizzazione dielettrica sulla punta della crepa) per previsioni ancora più accurate.

Insomma, capire e prevedere il comportamento delle crepe in questi materiali intelligenti è cruciale per renderli sempre più affidabili e performanti nelle tantissime applicazioni in cui già li usiamo e in quelle, ancora più futuristiche, che ci aspettano!

Fonte: Springer