Immagini Nitide in un Lampo? Il Trucco del Precondizionamento Svelato!

Ciao a tutti, appassionati di immagini e matematica! Oggi voglio parlarvi di qualcosa che mi sta particolarmente a cuore: come possiamo “ripulire” le nostre foto mosse o sfocate, un processo che in gergo chiamiamo image deblurring. Immaginate quella foto perfetta rovinata da un piccolo tremolio della mano, o un dettaglio importante perso nella sfocatura. Frustrante, vero? Fortunatamente, la matematica e l’informatica ci vengono in aiuto con modelli e algoritmi sempre più sofisticati.

Il Problema delle Immagini Mosse e gli Strumenti Matematici

Quando un’immagine è sfocata, matematicamente possiamo pensarla come il risultato di una “convoluzione” dell’immagine originale nitida con un operatore (il “blur”) più l’aggiunta di rumore (quelle imperfezioni casuali, tipo granulosità). Recuperare l’immagine originale è un tipico problema inverso, spesso “mal posto”, il che significa che piccole variazioni nei dati (la foto sfocata) possono portare a grandi differenze nella soluzione ricostruita. Serve un approccio robusto!

Qui entrano in gioco i modelli variazionali. L’idea è cercare un’immagine che sia un buon compromesso tra due esigenze:

• Fedeltà ai dati: L’immagine ricostruita, se ri-sfocata, deve assomigliare il più possibile alla foto mossa che abbiamo osservato. Spesso si usa la norma ( ell^2 ), che misura la differenza quadratica pixel per pixel.
• Regolarizzazione: L’immagine ricostruita deve avere delle proprietà “desiderabili”, come essere liscia o avere contorni netti. Questo termine, spesso non-smooth (cioè con “spigoli” matematici), introduce una conoscenza a priori su come dovrebbe apparire un’immagine naturale. Pensate alla Total Variation (TV), molto popolare per preservare i bordi.

Il tutto si traduce in un problema di ottimizzazione: minimizzare una funzione che somma questi due termini, bilanciati da un parametro ( lambda ).

Gli Algoritmi Classici e i Loro Limiti

Per risolvere questi problemi di ottimizzazione, si usano spesso metodi basati sul gradiente prossimale. Sono algoritmi iterativi del primo ordine (usano solo le derivate prime). L’idea base è alternare due passi:

1. Un passo di discesa lungo il gradiente della parte “liscia” (la fedeltà ai dati).
2. Un passo “prossimale” relativo alla parte non-liscia (la regolarizzazione), che cerca di “proiettare” la soluzione verso lo spazio delle immagini con le proprietà desiderate.

Algoritmi come ISTA o la sua versione accelerata FISTA rientrano in questa categoria. Funzionano bene e sono relativamente semplici, ma possono essere lenti a convergere, specialmente se il problema è complesso o mal condizionato.

Un’altra complicazione sorge quando il passo prossimale non ha una formula chiusa (come nel caso della Total Variation). Qui si ricorre a metodi più sofisticati, come gli approcci primale-duale, che riformulano il problema e lo risolvono in uno spazio più grande. Un esempio è l’algoritmo Nested Primal-Dual (NPD), che usa un ciclo interno (nested) per approssimare il passo prossimale. Figo, ma anche NPD può soffrire di convergenza lenta.

Accelerare le Cose: Metriche Variabili e Precondizionamento

Come possiamo dare una “svegliata” a questi algoritmi? Due strategie principali sono emerse:

• Metriche Variabili: Invece di usare la metrica standard (Euclidea) nel passo prossimale, si usa una metrica definita da una matrice ( P_n ) che cambia ad ogni iterazione. Questa matrice può incorporare informazioni del secondo ordine (simili all’Hessiana), guidando la convergenza più efficacemente. L’algoritmo NPDIT (Nested Primal-Dual Iterated Tikhonov) usa questa idea, scegliendo ( P_n ) ispirandosi ai metodi di Tikhonov.
• Precondizionamento: Questa è una tecnica classica per risolvere sistemi lineari ( Ax=b ). L’idea è moltiplicare il sistema a sinistra o a destra per una matrice “precondizionatrice” ( M ) (facile da invertire) in modo che il nuovo sistema (es. ( M^{-1}Ax=M^{-1}b )) sia più “facile” da risolvere per un metodo iterativo.

NPDIT ha mostrato ottime performance, superando altri metodi accelerati in alcuni scenari di deblurring con Total Variation. Tuttavia, ha un costo computazionale non trascurabile, specialmente nel ciclo interno per approssimare il passo prossimale con metrica variabile. Ogni iterazione interna richiede calcoli extra che coinvolgono l’inversa del precondizionatore ( P_n^{-1} ).

La Sorpresa: Destra vs. Sinistra nel Deblurring

Ed è qui che le cose si fanno *davvero* interessanti! Studiando NPDIT applicato specificamente al problema del deblurring (dove la fedeltà ai dati è ( frac{1}{2}Vert Au – b^{delta }Vert ^2 )), ci siamo accorti di una cosa: la strategia a metrica variabile di NPDIT è matematicamente equivalente a una strategia di precondizionamento a destra applicata all’algoritmo NPD base. In pratica, si modifica l’incognita ( u ) trasformandola in ( z = Ru ) (con ( P = R^T R )) e si risolve il problema per ( z ).

Questa osservazione apre una domanda naturale: se NPDIT è come un precondizionamento a destra, cosa succede se proviamo un precondizionamento a sinistra? L’idea sarebbe modificare direttamente il termine di fedeltà ai dati, usando una matrice ( S ) (legata a un precondizionatore primale ( P ) dalla relazione ( P = A^T S A )) per definire una nuova norma: ( frac{1}{2}Vert S^{1/2}(Au – b^{delta })Vert ^2 ).

PNPD: La Nostra Proposta Basata sul Precondizionamento a Sinistra

Abbiamo quindi sviluppato un nuovo algoritmo, che abbiamo chiamato Preconditioned Nested Primal-Dual (PNPD). Applichiamo l’algoritmo NPD al problema modificato con il precondizionamento a sinistra. La magia? L’iterazione che ne risulta è simile a NPDIT, ma con una differenza cruciale: il precondizionatore ( P ) (o ( S )) non influenza più il calcolo delle variabili duali nel ciclo interno!

Questo significa che il passo più costoso computazionalmente, l’approssimazione del proximity operator, torna ad essere quello standard (come in NPD), senza le moltiplicazioni extra per ( P^{-1} ) richieste da NPDIT ad ogni sotto-iterazione. Il risultato atteso? Una velocità di calcolo (CPU time) significativamente migliore, a parità (o quasi) di numero di iterazioni per raggiungere una certa accuratezza.

Abbiamo dimostrato la convergenza di PNPD verso la soluzione del problema *modificato* (quello con la norma indotta da ( S )). Una scelta comune e conveniente per ( P ) (e quindi ( S )) è ( P = A^T A + nu I ), dove ( nu > 0 ) è un parametro. Questa scelta soddisfa la condizione ( P = A^T S A ) (con ( S = AA^T + nu I )) e si collega ai metodi di Tikhonov.

Stabilità e Velocità: Il Dilemma del Parametro ν

C’è un però. La scelta di ( nu ) nel precondizionatore ( P = A^T A + nu I ) è un’arma a doppio taglio.

• Un ( nu ) piccolo rende ( P ) più simile all’Hessiana del termine di fedeltà ( A^T A ), il che può accelerare drasticamente la convergenza iniziale (è quasi come fare un passo di Newton).
• Tuttavia, se ( A^T A ) è mal condizionata (comune nel deblurring), un ( nu ) troppo piccolo rende ( P ) quasi singolare, e la sua inversione ( P^{-1} ) nell’algoritmo può introdurre instabilità numerica, facendo “impazzire” le iterazioni.

Bisogna trovare un compromesso.

Soluzioni Intelligenti: k_max, Niente Extrapolation e Precondizionatori Dinamici

Come gestire questo trade-off? Abbiamo esplorato alcune strategie:

1. Aumentare ( k_{textrm{max}} ): Fare più iterazioni nel ciclo interno (aumentare ( k_{textrm{max}} )) per calcolare più accuratamente il passo prossimale può stabilizzare l’algoritmo anche per ( nu ) piccoli. Ovviamente, aumenta il costo per iterazione esterna.
2. Rimuovere l’Extrapolation (PNPD_NE): Gli algoritmi tipo FISTA usano un passo di “estrapolazione” (o inerzia) per accelerare. Rimuovendo questo passo (( gamma_n = 0 )), l’algoritmo diventa meno aggressivo e più stabile, anche se potenzialmente più lento in termini di numero di iterazioni. Lo abbiamo chiamato PNPD_NE (No Extrapolation).
3. Precondizionatori Non Stazionari: E se ( nu ) cambiasse ad ogni iterazione ( n )? Possiamo usare una sequenza ( nu_n ) che magari parte da un valore piccolo (per accelerare all’inizio) e poi cresce, rendendo ( P_n = (1-nu_n)A^T A + nu_n I ) più stabile nelle fasi successive. Abbiamo testato sequenze ( nu_n ) decrescenti, crescenti, e una “bootstrap” che cresce rapidamente fino a ( nu_n = 1 ) (il che significa che ( P_n ) diventa l’identità, e PNPD diventa essenzialmente NPD dopo un certo numero di iterazioni). Questo approccio permette anche di convergere alla soluzione del problema *originale* (con la norma ( ell^2 )), perché ( P_n rightarrow I ) implica ( S_n rightarrow I ).

Vediamo Come Funziona: I Risultati Numerici

Abbiamo messo alla prova PNPD, confrontandolo con NPD e NPDIT su diversi problemi di image deblurring (immagini diverse, tipi di blur, livelli di rumore). I risultati confermano le nostre aspettative:

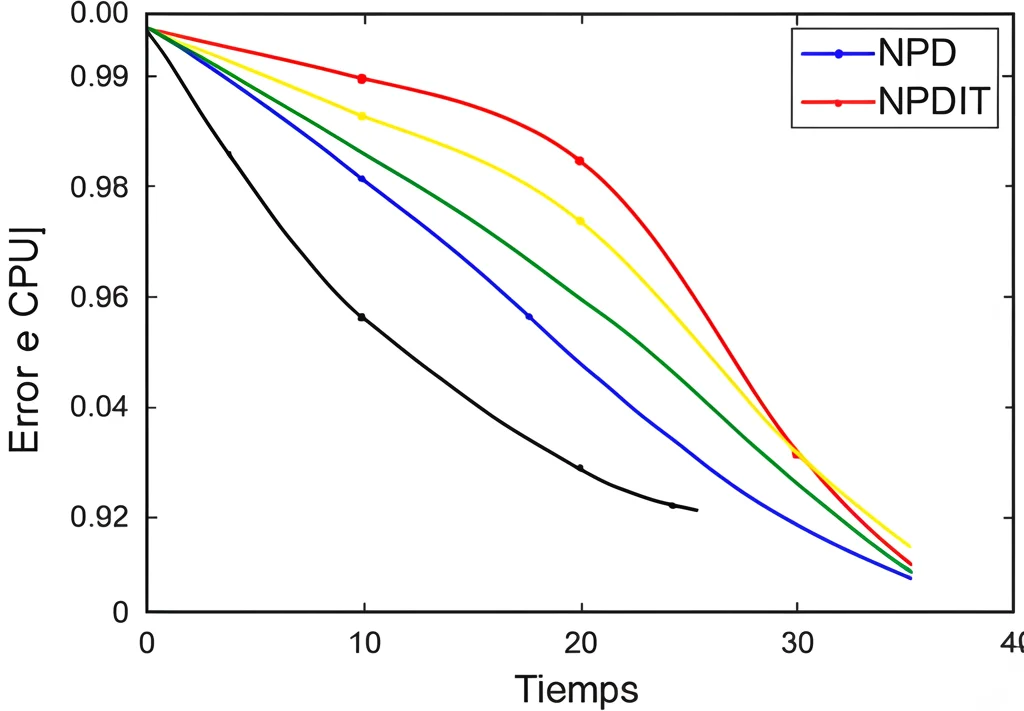
• Velocità CPU: PNPD è costantemente più veloce di NPDIT in termini di tempo di calcolo totale. Il vantaggio aumenta all’aumentare di ( k_{textrm{max}} ), come previsto. Entrambi sono molto più veloci di NPD.
• Convergenza Iterazioni: PNPD e NPDIT mostrano un numero di iterazioni simile per raggiungere una data qualità di ricostruzione, entrambi nettamente migliori di NPD.
• Qualità Ricostruzione: La qualità delle immagini ricostruite da PNPD è paragonabile a quella di NPDIT.
• Stabilità e Strategie: Abbiamo confermato l’instabilità di PNPD per ( nu ) piccoli e ( k_{textrm{max}} ) basso. Aumentare ( k_{textrm{max}} ) o usare PNPD_NE risolve il problema, al costo di un po’ di velocità (CPU o iterazioni). Le strategie non stazionarie, in particolare la “bootstrap”, si sono dimostrate molto promettenti, offrendo un buon bilanciamento tra velocità iniziale e stabilità/convergenza al problema originale.

Insomma, i numeri parlano chiaro: il precondizionamento a sinistra (PNPD) sembra offrire un vantaggio tangibile in termini di efficienza computazionale per questo tipo di problemi.

Conclusioni e Prospettive Future

In conclusione, abbiamo proposto PNPD, un algoritmo precondizionato a sinistra per l’ottimizzazione convessa composita, motivato dal problema dell’image deblurring. Abbiamo mostrato che è interpretabile come un precondizionamento a sinistra dell’algoritmo NPD e che, rispetto all’approccio a metrica variabile/precondizionamento a destra (NPDIT), offre un significativo risparmio computazionale senza sacrificare la qualità della ricostruzione o la velocità di convergenza in termini di iterazioni. Le strategie per gestire la stabilità, inclusi i precondizionatori non stazionari, lo rendono uno strumento flessibile e potente.

Cosa ci riserva il futuro? Sicuramente esplorare altre scelte per la matrice di precondizionamento ( P ), specialmente in contesti dove ( A^T A + nu I ) potrebbe essere costoso da gestire (pensiamo alla Tomografia Computerizzata). Inoltre, studiare l’interazione tra precondizionamento e altre tecniche di accelerazione (come diverse strategie di estrapolazione) potrebbe portare a ulteriori miglioramenti. Il viaggio per ottenere immagini perfette continua!

Fonte: Springer