Somme di Pareto: Come Trovare le Scelte Ottimali Senza Impazzire (e con Algoritmi Nuovi!)

Ciao a tutti! Oggi voglio parlarvi di un problema affascinante che mi ha tenuto impegnato per un po’: come combinare insiemi di soluzioni “ottimali” per trovarne di nuove, ancora migliori. Immaginate di dover scegliere, ad esempio, un percorso in auto valutando sia il tempo che la distanza. Non c’è una singola risposta “migliore” in assoluto, ma un insieme di compromessi validi: magari un percorso è velocissimo ma lungo, un altro è corto ma lento, e altri stanno nel mezzo. Questi compromessi formano quello che chiamiamo un insieme di Pareto.

Ora, cosa succede se abbiamo due di questi insiemi di soluzioni ottimali (diciamo, per due tratti di strada consecutivi) e vogliamo combinarli per trovare le soluzioni ottimali per il percorso completo? Qui entra in gioco la somma di Minkowski: in pratica, sommiamo ogni soluzione del primo insieme con ogni soluzione del secondo. Il problema è che questa somma può diventare gigantesca! Se i nostri insiemi iniziali hanno n soluzioni ciascuno, la somma di Minkowski ne ha n². Un sacco di roba da calcolare e memorizzare.

Ma ecco il punto cruciale: molte di queste soluzioni combinate non sono affatto ottimali! Vengono “dominate” da altre (cioè, c’è un’altra soluzione combinata che è migliore sotto tutti i punti di vista). L’insieme delle soluzioni combinate che *non* sono dominate da nessun’altra è ciò che chiamiamo la somma di Pareto. E la buona notizia è che questa somma di Pareto (che chiameremo C) può essere molto, molto più piccola di n², a volte persino più piccola di n!

La sfida, quindi, è: come calcolare questa benedetta somma di Pareto C senza dover prima generare e filtrare l’intera, enorme somma di Minkowski M? È proprio su questo che mi sono concentrato.

Perché è Importante? Un Esempio Concreto: La Pianificazione di Percorsi

Vi chiederete: “Ma a cosa serve tutto questo?”. Beh, un’applicazione super pratica è la pianificazione di percorsi stradali multi-obiettivo. Pensate a Google Maps o simili, ma dove non volete solo il percorso più veloce o più corto, ma un insieme di opzioni che bilanciano diversi criteri (tempo, distanza, pedaggi, consumo energetico, pendenza…).

Gli algoritmi più avanzati per fare questo, come le Gerarchie di Contrazione (CH) bi-criterio, funzionano pre-elaborando la rete stradale. Creano delle “scorciatoie” (shortcut) che rappresentano i percorsi ottimali (in senso di Pareto) tra due punti. Quando si crea una nuova scorciatoia combinando due esistenti, indovinate un po’? Bisogna calcolare proprio la somma di Pareto dei loro insiemi di costo! Se lo facciamo in modo ingenuo (calcolando tutta la somma di Minkowski), la pre-elaborazione diventa lentissima e richiede troppa memoria, specialmente per reti stradali grandi. Trovare algoritmi veloci ed efficienti in termini di spazio per la somma di Pareto è quindi fondamentale per rendere questi sistemi di navigazione avanzati una realtà.

I Limiti della Velocità: Cosa Ci Dice la Teoria

Prima di tuffarmi nella creazione di nuovi algoritmi, mi sono chiesto: quanto veloci *possiamo* sperare di essere? Esiste un limite teorico? Ebbene sì. Ho scoperto (o meglio, dimostrato, basandomi su congetture consolidate nel campo della complessità computazionale, come quella sulla convoluzione (min,+)) che è molto improbabile riuscire a calcolare la somma di Pareto in tempo significativamente inferiore a O(n²) quando la dimensione dell’output k (cioè il numero di punti nella somma di Pareto finale) è dell’ordine di n o più grande. In parole povere: se l’insieme risultato è abbastanza grande, non aspettatevi miracoli sub-quadratici. Questo ci dà un’importante linea guida: dobbiamo puntare ad algoritmi che si avvicinino a O(n²) nel caso peggiore, ma che siano magari più veloci quando l’output k è piccolo, e soprattutto che non usino troppa memoria!

La Mia Cassetta degli Attrezzi: Nuovi Algoritmi per la Somma di Pareto

Armato di queste conoscenze, ho sviluppato e analizzato diversi approcci. Ecco una panoramica:

• Algoritmi di Base (con un pizzico di ingegneria): Ho iniziato con approcci più semplici. Uno chiamato Sort e Compare (SC) si è rivelato molto interessante. L’idea è di generare gli elementi della somma di Minkowski in un ordine specifico (lessicografico) usando una struttura dati efficiente (una min-heap) e scartare al volo quelli dominati. Questo raggiunge un tempo di O(n² log n) usando solo O(n+k) spazio – ottimo perché lo spazio dipende dall’output k e non dal gigantesco n²! Ho anche aggiunto delle ottimizzazioni pratiche per velocizzarlo ulteriormente.
• Algoritmi Successivi (la vera novità): Qui le cose si fanno più furbe. L’idea è: invece di generare tutto e poi filtrare, perché non troviamo i punti della somma di Pareto uno dopo l’altro? Partiamo dai due punti estremi (quello con la x minima e quello con la y minima, che sono sempre nella somma di Pareto). Poi, cerchiamo il “prossimo” punto della somma di Pareto in modo intelligente, restringendo l’area di ricerca. Ho sviluppato un algoritmo chiamato Successive Sweep Search (SSS) che fa proprio questo. Usa un “oracolo” che trova l’elemento minimo in un certo intervallo della matrice della somma di Minkowski, ma lo fa con uno “sweep” (una passata) molto efficiente, senza materializzare l’intera matrice. Il bello è che SSS ha un tempo di O(n log n + nk) e spazio O(n+k) (o addirittura O(n) se l’output viene trasmesso in streaming). Questo significa che se k è piccolo (molto meno di n), SSS è sub-quadratico! Batte il limite teorico? No, perché quel limite valeva per k grande. Ma per output piccoli, è una bomba! Anche qui, ho introdotto tecniche di “skipping” per accelerarlo in pratica.

Alla Prova dei Fatti: Gli Esperimenti

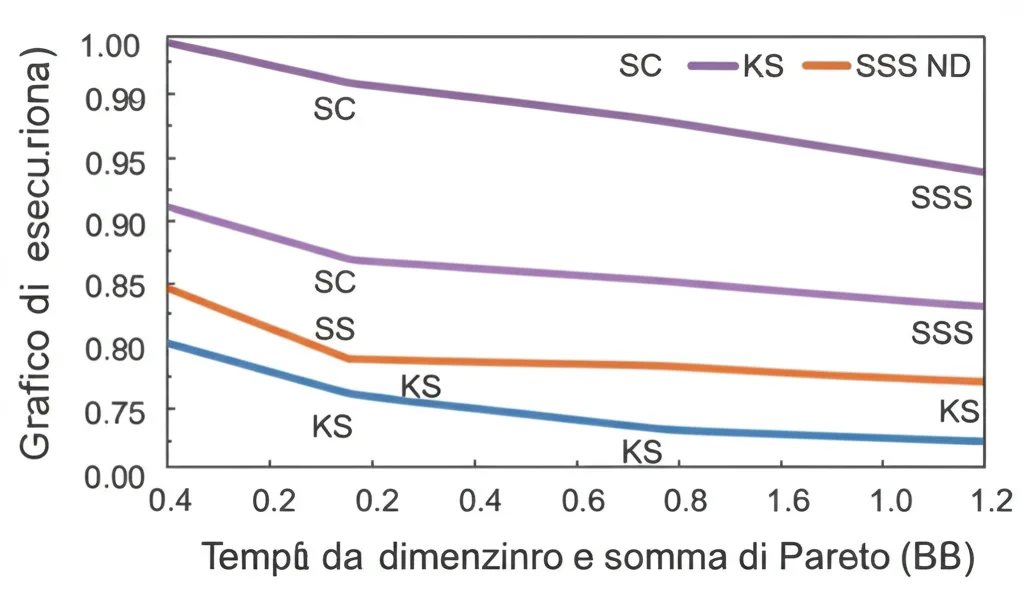
Naturalmente, la teoria è bella, ma come si comportano questi algoritmi nel mondo reale? Ho condotto una vasta campagna di esperimenti, confrontando i miei nuovi algoritmi (SC, SSS e varianti) con quelli esistenti (come l’algoritmo di Kirkpatrick-Seidel – KS, e NonDomDC – ND) e anche con un approccio basato su strutture dati chiamate Pareto Trees. Ho usato sia dati generati casualmente (con diverse distribuzioni, alcune delle quali creano somme di Pareto piccole, altre enormi) sia dati reali provenienti proprio dalla pianificazione di percorsi su reti stradali (OpenStreetMap).

I risultati sono stati elettrizzanti!

• L’algoritmo Sort e Compare (SC), specialmente nella sua versione “ingegnerizzata”, si è dimostrato incredibilmente robusto e spesso il più veloce in assoluto, soprattutto quando la somma di Pareto risultante era grande. Ha surclassato gli approcci precedenti (KS, ND) anche di ordini di grandezza!
• L’algoritmo Successive Sweep Search (SSS) ha brillato quando la somma di Pareto era piccola rispetto alla dimensione della somma di Minkowski (cioè k piccolo). Questo è esattamente ciò che succede spesso nei dati reali di route planning! Infatti, nell’applicazione sulle reti stradali, SSS è risultato il campione indiscusso, riducendo drasticamente i tempi di pre-elaborazione e anche di risposta alle query rispetto agli altri metodi.
• Un aspetto fondamentale è che i miei nuovi algoritmi (SC e SSS) garantiscono un consumo di spazio sensibile alla dimensione dell’output (O(n+k)), a differenza di approcci come KS che richiedono sempre spazio O(n²). Questo è un vantaggio enorme per problemi di grandi dimensioni.
• Le tecniche di ingegnerizzazione (come il pruning in SC o lo skipping in SSS) hanno dato un boost significativo alle prestazioni pratiche.

In Conclusione: Un Passo Avanti per l’Ottimizzazione

Questa ricerca è stata un viaggio affascinante nel mondo degli algoritmi e della geometria computazionale. Abbiamo dimostrato limiti teorici importanti per il problema della somma di Pareto e, cosa più importante, abbiamo sviluppato nuovi algoritmi (SC e SSS) che non solo rispettano questi limiti ma offrono anche prestazioni eccellenti nella pratica, specialmente grazie al loro basso consumo di memoria.

L’impatto sull’applicazione della pianificazione di percorsi bi-criterio è tangibile: ora possiamo affrontare istanze più grandi e ottenere risultati più velocemente. Ma le implicazioni vanno oltre: ovunque ci sia bisogno di combinare insiemi di soluzioni multi-obiettivo in modo efficiente (programmazione dinamica, ottimizzazione combinatoria, ricerca locale multi-obiettivo), questi nuovi strumenti potrebbero fare la differenza.

Cosa riserva il futuro? Ci sono ancora domande aperte: si può eliminare quel fattore logaritmico nel tempo di SC? Esistono algoritmi sub-quadratici per casi medi o “smussati”? Come si comportano questi approcci in dimensioni superiori a due? E la parallelizzazione? Tante strade ancora da esplorare! Ma per ora, sono entusiasta dei progressi fatti e spero che questi algoritmi possano aiutare altri ricercatori e sviluppatori ad affrontare problemi complessi di ottimizzazione.

Fonte: Springer